4. Решение основных типовых задач

Перейдем к рассмотрению типовых задач.

Пример 5: упростить выражение:

Итак, приведем новый одночлен к стандартному виду – получим численный коэффициент и буквенную часть:

Пример 6: упростить выражение:

Выполним возведение одночленов в степень, после этого упростим числитель – умножим одночлены, затем выполним деление:

Пример 7: решить уравнение:

Буквенная часть одночленов одинаковая, значит, мы имеем право их сложить:

В этом элементарном уравнении очевиден ответ:

Нам было задано простейшее уравнение и требовалось только найти его корень, но чаще это уравнение сперва нужно составить – как, например, при решении текстовых задач.

Пример 8: туристы были в походе 3 дня. В первый день они прошли   всего пути, во второй день   оставшегося пути, и в третий день 25 км. Найти общую длину пути.

Для решения задачи применим метод математического моделирования.

Этап 1 – составление математической модели:

Обозначим весь пройденный туристами путь за х километров, в таком случае, в первый день они прошли   километров, таким образом, им осталось пройти   километров, тогда во второй день они прошли треть оставшегося пути –  , и в третий день 25 километров. Составим схему (рис. 1):

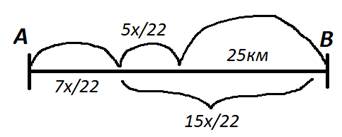
Рис. 1

Запишем общий путь в виде уравнения:

Математическая модель составлена.

Этап 2 – работа с математической моделью: найдем корни составленного уравнения. Все неизвестные перенесем влево, а свободные члены – вправо:

В левой части его стоят одночлены с одинаковой буквенной частью – имеем право их сложить:

Сократим дробь:

Умножим обе части уравнения на 11:

Разделим обе части уравнения на 5:

Этап 3 – ответ на вопрос задачи: мы нашли  , за х было принято расстояние, пройденное туристами, что и нужно было найти в задаче, таким образом, даем ответ: путь, пройденный туристами, составляет 55 километров.

Рассмотрим шуточную задачу.

Пример 9: задумайте число. Прибавьте к нему 10. Отнимите 2. Отнимите задуманное число. Прибавьте 10. Вы получили число 18?

Каким образом получился такой «фокус»? мы попросили человека задумать число, а через несколько действий задуманное число отнять, опишем последовательность, обозначив задуманное число за х:

Упростив выражение, получаем 18, то есть независимо от задуманного числа вы можете предугадать результат, запоминая заданные числа.

Задачу можно усложнить:

Задумайте число. Прибавьте 10. Умножьте результат на 2. Прибавьте 10. Отнимите задуманное число. Прибавьте 10. Отнимите задуманное число. Прибавьте 10.

Опишем последовательность, обозначив число за х:

Упростим полученное выражение:

Результат снова не зависит от задуманного числа, нужно только запомнить, что вы попросили прибавлять и отнимать.

5. Выводы по уроку

Вывод: на данном уроке мы вспомнили основные определения и свойства одночленов, типовые задачи, с ними связанные. Мы решили различные примеры, чтобы вспомнить и окончательно закрепить технику работы с одночленами.

Домашнее задание.

1. Преобразуйте выражение в одночлен стандартного вида: а) ; б) .

2. Упростите выражение: .

Урок 3: Повторение. Многочлены.

На данном уроке мы вспомним определение многочлена и приведение его к стандартному виду. Также вспомним основные арифметические операции над многочленами и решим типовые задачи.