4. Диференціювання сигналу

Подивимося, як впливає на спектр диференціювання сигналу в часовій області. Для цього нам доведеться скористатися визначенням поняття похідної:

.

Застосуємо до цього виразу перетворення Фур’є:

.

Спектр похідної обчислюється множенням спектру вихідного сигналу на jω. Таким чином, при диференціюванні низькі частоти ослабляються, а високі посилюються. Фазовий спектр сигналу зсувається на 90° для позитивних частот і на - 90° для негативних. Множник jω називають оператором диференціювання сигналу в частотній області.

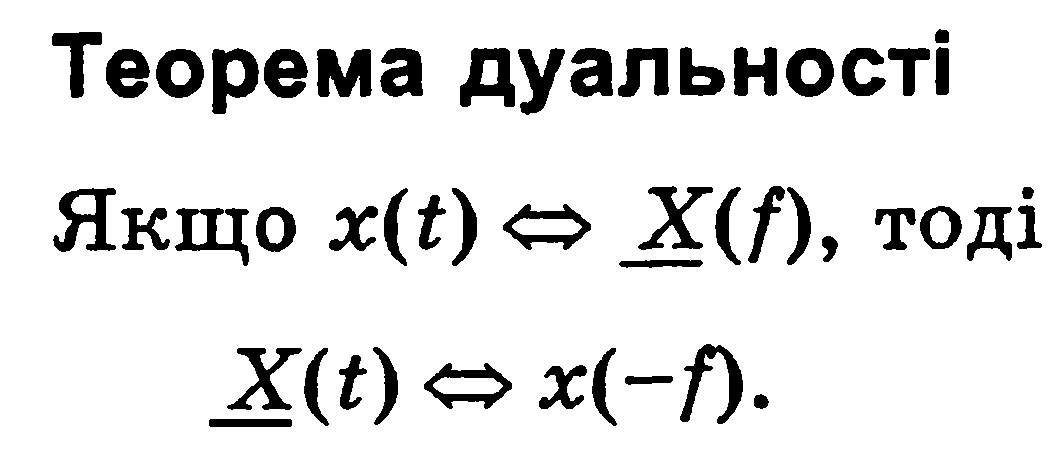
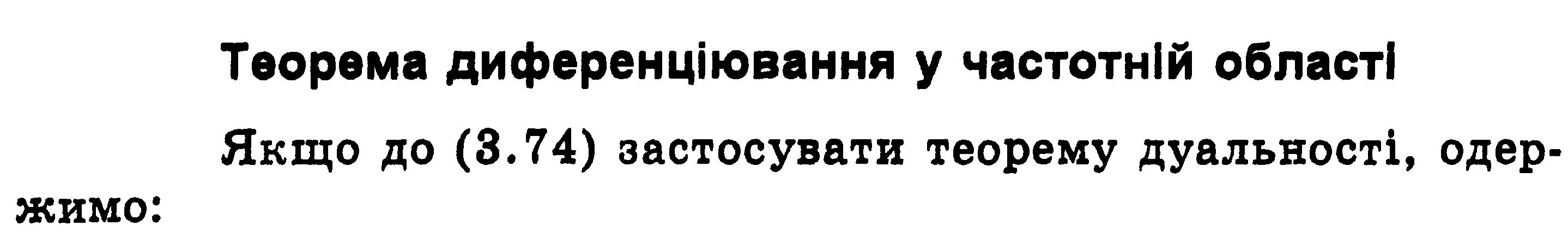
Звідки випливає Теорема множення сигналу на t:

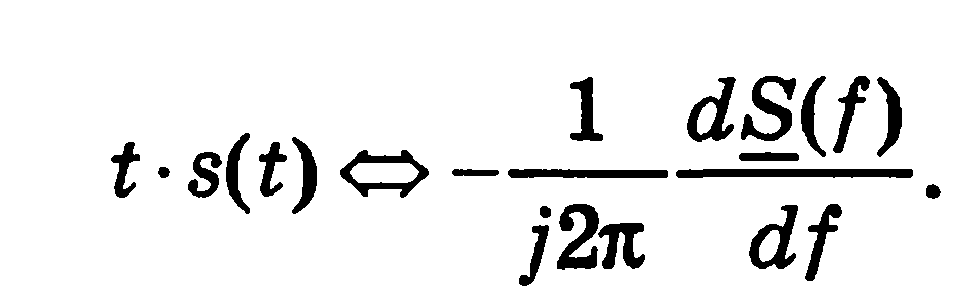
5. Інтегрування сигналу

Інтегрування, як відомо, є операцією, оберненою до диференціювання. Тому, виходячи з результатів, отриманих в попередньому розділі, здавалося б, можна очікувати наступний результат:

.

Проте усе не так просто. Детальний аналіз, виконаний, наприклад, в [1], показує, що ця формула справедлива лише для сигналів, що не містять постійної складової, у яких

.

В загальному ж випадку результат повинен містити також доданок у вигляді дельта-функції на нульовій частоті. Множник перед дельта-функцією пропорційний постійній складовій сигналу

.

Отже, при інтегруванні вихідного сигналу високі частоти ослабляються, а низькі посилюються. Фазовий спектр сигналу зміщується на - 90° для позитивних частот і на 90° для негативних. Множник 1/(jω) називають оператором інтегрування в частотній області.

6. Спектр згортки сигналів

Згортка сигналів є дуже часто використовуваною в радіотехніці інтегральною операцією, оскільки вона описує, зокрема, проходження сигналу через лінійну систему з постійними параметрами (детальніше це обговорюватиметься в розділі 6) :

Піддамо таку конструкцію перетворенню Фур'є:

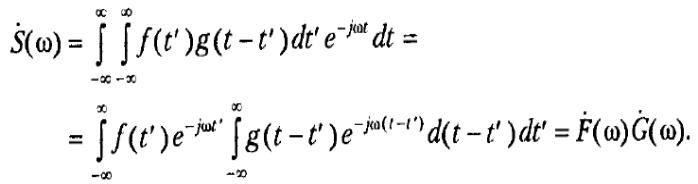
Отриманий результат дуже важливий, він часто використовується на практиці: спектр згортки дорівнює добутку спектрів.

У випадку, коли сигнал можна кожну з цих функцій представити їх оберненими перетвореннями Фур’є від відповідних спектральних густин кожного з сигналів

,

і отримати наступне співвідношення

Інтеграл у квадратних дужках по змінній t є спектральною густиною функції при частоті , тобто , звідки маємо

.

Таким чином, спектр добутку двох функцій часу дорівнює (з коефіцієнтом 1/2π) згортці їх спектрів і , де

або інакше

.

Неважко переконатися, що операція згортки комутативна

.

7. Множення сигналу на гармонійну функцію

Помножимо вихідний сигнал f(t) , спектр якого нам відомий, на гармонійну функцію: і подивимося, що сталося із спектром сигналу:

.

Як бачите, спектр "роздвоївся" - розпався на два доданки удвічі меншого рівня (множник 1/2), зміщених на праворуч і ліворуч по осі частот. Крім того, при кожному доданку є множник, що враховує початкову фазу гармонійного коливання. З практичним застосуванням цієї властивості ми вже певною мірою стикалися на лабораторній роботі і ще матимемо справу при обговоренні властивостей сигналів з амплітудною модуляцією.