Лекція 4
Тема 4. Інтегральне перетворення Фур’є
1. Пряме перетворення. Обернене перетворення. Властивості інтегрального перетворення Фур'є.
На минулій лекції та лабораторній роботі ми розглядали розкладання періодичних сигналів в ряд Фур’є. Метод рядів Фур’є може бути узагальнений і на випадок неперіодичних сигналів. Для цього згадаємо вигляд комплексної форми представлення ряду Фур'є
Коефіцієнти
обчислюються
за формулою
°
.
Використаємо цю форму ряду Фур’є для отримання спектрального представлення неперіодичного сигналу.
Нехай аналізований сигнал s(t) є імпульсним сигналом обмеженої тривалості. Якщо уявно доповнити цей сигнал послідовністю таких самих сигналів з періодом Т, тоді такий сигнал може бути представлений рядом Фур’є
(1)
з коефіцієнтами . (2)
Для повернення до одиночного імпульсу слід спрямувати період Т цієї послідовності до нескінченності при цьому матимемо:
1. Частоти
сусідніх гармонік
і
будуть скільки завгодно близькими, тому
у попередніх двох формулах дискретну
змінну
можна змінити на
неперервну
- поточну частоту, а значення частоти
.
2.
Амплітудні коефіцієнти
стануть
необмежено малими, оскільки у знаменнику
(2) є нескінченно велике значення періоду
Т
.
Запишемо ряд (1) для цього випадку
,
тут
ураховано, що
.
Таким
чином ми отримали подвійний інтеграл.
Внутрішній інтеграл є спектральною густиною сигналу s(t), яка обчислюється за допомогою перетворення Фур’є:
.
(3)
Також з цього граничного представлення сигналу s(t) маємо й обернене перетворення Фур’є для цього сигналу
.
(4)
Якщо використовувати не кругову частоту ω, а звичайну циклічну частоту f, формули прямого і оберненого перетворення Фур'є стають ще більш симетричними, відрізняючись лише знаком у показнику експоненти:
;
.
Як ми вже згадували на першій лекції, спектральну густину можна представити через її модуль і аргумент:
Модуль і аргумент спектральної густини визначають відповідно за формулами:
,
θ(ω)
= arg S
(ω)=
,
де
A(ω)=
та
B(ω)
.
Умови існування спектральної густини сигналу.
Для
існування спектральної густини сигналу
s(t)
(3),
,
як
це доведено в математиці, необхідне
виконання двох умов:
на будь-якому кінцевому інтервалі функція s(t) повинна задовольняти умовам Діріхле;
функція s(t) абсолютно інтегрована на усій числовій осі, тобто
Остання умова значно звужує клас допустимих сигналів. Наприклад, гармонійний сигнал, який існує на нескінченній осі часу не є абсолютно інтегрованим. Однак, завдяки застосуванню узагальнених функцій (Хевісайда, Дірака), також вдається обчислювати спектральні густини неінтегрованих сигналів, в тому числі періодичних сигналів, що буде застосовуватись нами в подальшому.
Якщо аналізований сигнал s(t) - дійсна функція, то відповідна йому спектральна густина (функція) S(ω) є "спряжено-симетричною" відносно нульової частоти. Це означає, що значення спектральної густини (функції) на частотах ω і – ω є комплексно-спряженими по відношенню одне до одного:
S(- ω) = S*(ω).
Якщо s(t) - парна функція, то, як і у разі ряду Фур'є, спектр буде чисто дійсним (і, отже, буде парною функцією). Якщо, навпаки, s(t) - функція непарна, то спектральна функція S(ω) буде чисто уявною (і непарною).
Модуль спектральної функції часто називають амплітудним спектром, а її аргумент - фазовим спектром. Легко показати, що для дійсного сигналу амплітудний спектр є парним, а фазовий - непарною функцією частоти:
|S(- ω) |=|S(ω) |, θ(- ω) = -θ(ω).
Отже, перетворення Фур'є (3) ставить у відповідність сигналу, заданому в часі, його спектральну функцію (густину). При цьому здійснюється перехід з часової області в частотну. Перетворення Фур'є є взаємно-однозначним, тому представлення сигналу в частотній області (спектральна функція) містить рівно стільки ж інформації, скільки і вихідний сигнал, заданий в часовій області.
Розглянемо приклади розрахунку перетворення Фур'є для деяких сигналів, що часто зустрічаються при рішенні різних задач.
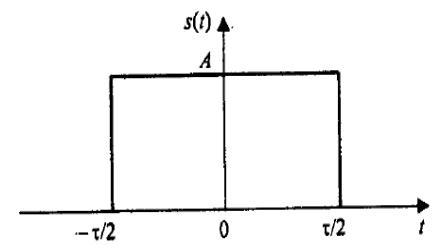
Прямокутний імпульс
Почнемо з прямокутного імпульсу, що центрується відносно початку відліку часу (рис. 1):
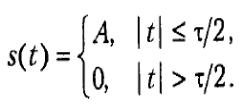
Рис. 1. Прямокутний імпульс
Обчислюємо спектральну функцію:
.
Остаточно маємо
.
(5)
Як бачите, спектр є функцією виду sіn(х)/х (рис. 2). Амплітудний спектр має пелюстковий характер, і ширина пелюсток рівна 2π/τ, тобто обернено пропорційна тривалості імпульсу. Значення спектральної густини на нульовій частоті дорівнює площі імпульсу - Аτ. Спектральна функція є дійсною, тому фазовий спектр набуває лише два значення - 0 і π, залежно від знаку функції sіn(х)/х. Значення фази π і –π однакові, різні знаки для фазового спектру при ω > 0 і ω < 0 використані лише з метою представити його у вигляді непарної функції.
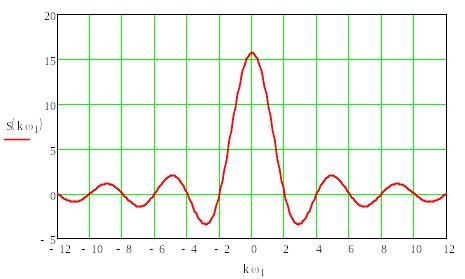
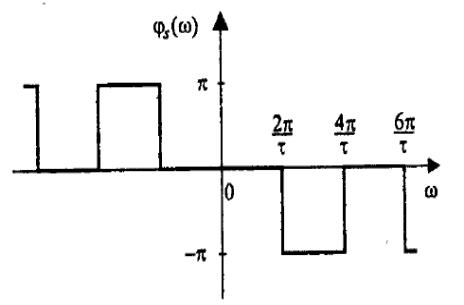
Рис. 2. Спектральна густина і фазовий спектр прямокутного відеоімпульсу
з параметрами: τ=π с; A=5 В
На
графіку
.
Тепер подивимось, що зміниться після зміщення імпульсу в часі. Нехай імпульс починається в нульовий момент часу (рис. 3) :
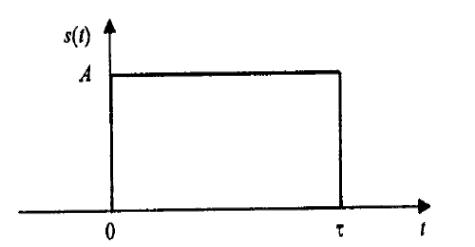
Рис. 3. Прямокутний імпульс із затримкою у часі
Обчислимо перетворення Фур’є і побудуємо графіки амплітудного і фазового спектрів (рис. 4), ураховуючи, що sin x = (ejx - e-jx)/2j.
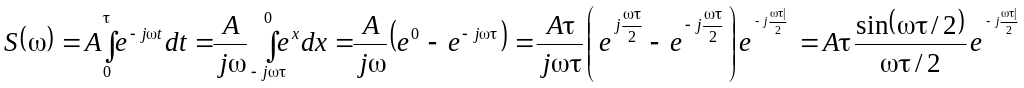.(6)
Цей приклад демонструє прояв властивості перетворення Фур’є, що стосується зміни спектру при зміщенні сигналу в часі. Ця властивість в загальному вигляді буде розглянута далі, в розділі "властивості перетворення Фур’є".
Рис. 4. Амплітудний і фазовий спектри прямокутного імпульсу із затримкою
З формули (6) і графіків (рис. 4) видно, що після зміщення імпульсу в часі його амплітудний спектр залишився тим самим, а фазовий отримав лінійно залежний від частоти зсув .
Строго кажучи, спектр цього сигналу тягнеться до нескінченності, лише поступово затухаючи. Тому вводять поняття ефективної ширини спектру. Як видно з графіків, спектр має пелюстковий характер і ширина головного пелюстка дорівнює 2π/τ. При пелюстковому характері спектру за ефективну ширину спектру можна прийняти ширину головного пелюстка. З графіків видно, що вона складає 2π/τ, тобто обернено пропорційна тривалості імпульсу. Це загальне співвідношення: чим коротше сигнал, тим ширше його спектр. Добуток же ефективних значень тривалості сигналу і ширини його спектру (він має назву бази сигналу) залишається рівним деякій константі, залежній від конкретного способу визначення цих параметрів. У нашому прикладі цей добуток, очевидно, дорівнює 2π. Взагалі, для сигналів простої форми (що не мають складної внутрішньоімпульсної структури) величина бази незалежно від способу визначення ефективних значень тривалості і ширини спектру складає декілька одиниць.
Тривалість сигналу і ширина його спектру підкоряються співвідношенню невизначеності, тобто добуток цих параметрів (база сигналу) не може бути меншим за одиницю. Обмежень максимального значення бази сигналу не існує. Звідси витікає, що можна сформувати сигнал великої тривалості, що одночасно має і широкий спектр (такі сигнали називають широкосмуговими, або складними, або сигналами з великою базою). А ось короткий сигнал з вузьким спектром, згідно із співвідношенням невизначеності, існувати не може.