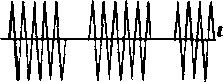Осцилограма амплітудно-маніпульованого сигналу
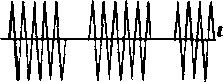
Нехай,
наприклад, функція
s(t)
є періодична послідовність відеоімпульсів,
розглянута вище (див. рис. 2). Вважаючи,
що амплітуда цих імпульсов А = 1, при
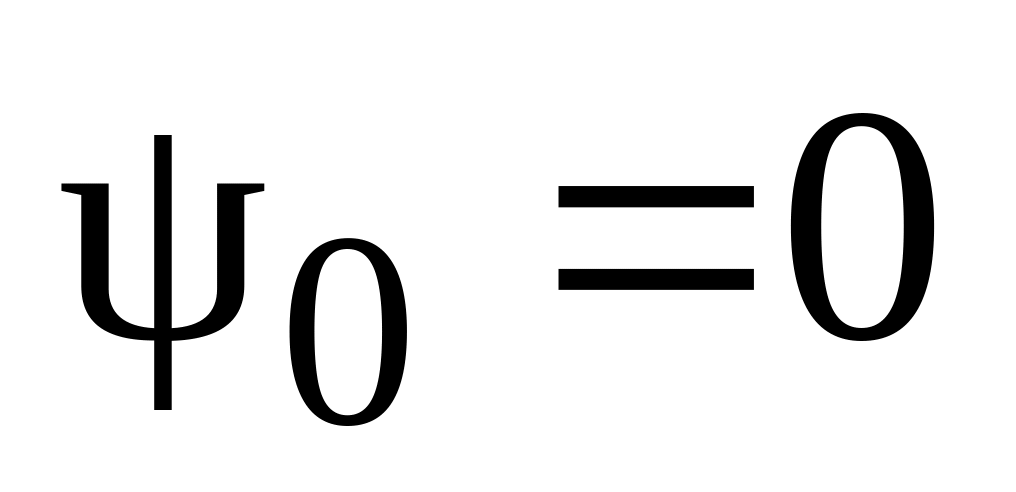маємо
де q
- шпаруватість послідовності. Фактично
ми комплексний амплітудний
спектр періодичної послідовності
прямоктних
імпульсів
(3) зсунутий на частоту несучої частоти
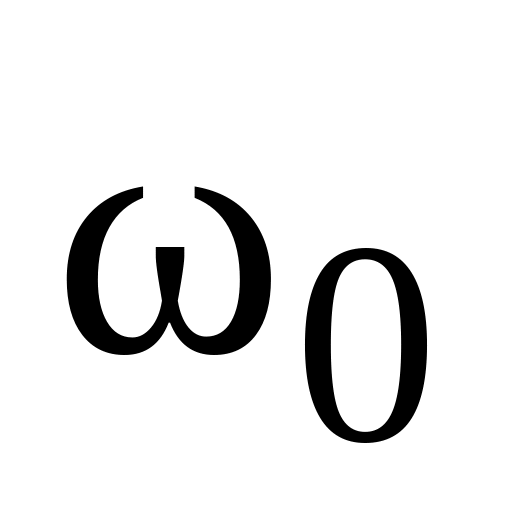(див.
рис. 3,б). Це дозволить нам використовувати
спеутроаналізатор, який функціонує в
діапазоні частот значно вищих за 0, для
дослідження спектрів послідовностей
імпульсів різної форми на лабораторному
занятті. Як бачимо, у цьому випадку
частоти, які відповідають від’ємним
індексам можуть бути наявні в реальному
спектрі сигналу, тому на практиці ми
маємо можливість спостерігати комплексну
форму ряду Фур’є послідовності імпульсів,
яка є огинаючою, наприклад, радіосигналу.
ЛІТЕРАТУРА
1. Цифровая обработка сигналов / А. Б. Сергиенко — СПб.: Питер, 2002. — 608 с: ил.. (Электронный ресурс)
2. Волощук Ю.Л. Сигнали та процеси в радіотехніці том. 1. - Харків: «СМІТ», 2003.
3. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. – 512 с.
4. Баскаков С.И. Радиотехнические цепи и сигналы. - М.: «Высшая школа» 2003.
5. Сато Ю. Обработка сигналов. Первое знакомство. – ОΔЕКА, 1999. – 175 с.