Лекція 3

Тема 3. Розкладання в ряд Фур’є періодичних сигналів

1. Умови Діріхле. Три форми запису ряду Фур’є. Теорема Парсеваля. Властивості розкладання в ряд Фур'є.

На минулій лекції ми розглянули питання перетворення аналогового сигналу у дискретний сигнал і умови, за яких є можливість відновлення з дискретного сигналу – аналогового без втрати інформації.

Для яких сигналів існує така можливість? (з обмеженим спектром). Якою теоремою це доведено (Котельникова, Найквиста-Шеннона)? Який вигляд має відновлений із застосуванням ряду Котельникова дискретизований сигнал з обмеженим спектром? ( .)

На минулій лекції вказувалося, що у загальному випадку відтворююча функція може бути представлена апроксимуючим поліномом

, (1)

де система базисних функцій.

У практиці обробки сигналів базисні функції частіш за все обирають ортогональними (тобто скалярний добуток ортогональних базисних функцій , c=const, для ортонормованих базисних функцій – c=1). Збіжність ряду до функції забезпечується при тому на практиці при обмеженні кількості членів ряду потрібно оцінювати похибку відновлення, щоб забезпечити її значення не гірше допустимого.

Якщо система базисних функцій ортонормована на відрізку часу , тобто

тоді представлення сигналу у вигляді (1’) називається узагальненим рядом Фур’є. Коефіцієнти цього ряду можна знайти множенням обох частин рівняння на базисну функцію, наприклад з індексом k, і подальшим інтегруванням рівняння за часом на інтервалі

.

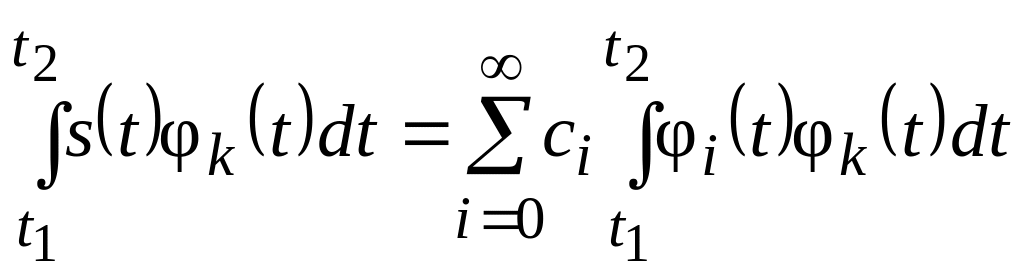З умови ортонормованісті базисних функцій, у правій частині рівняння залишиться лише один член суми з номером k

.

Сукупність коефіцієнтів узагальненого ряду Фур’є називається спектром сигналу за ортонормованою системою базисних функцій . Спектр повністю визначає сигнал . Для ортогональної системи .

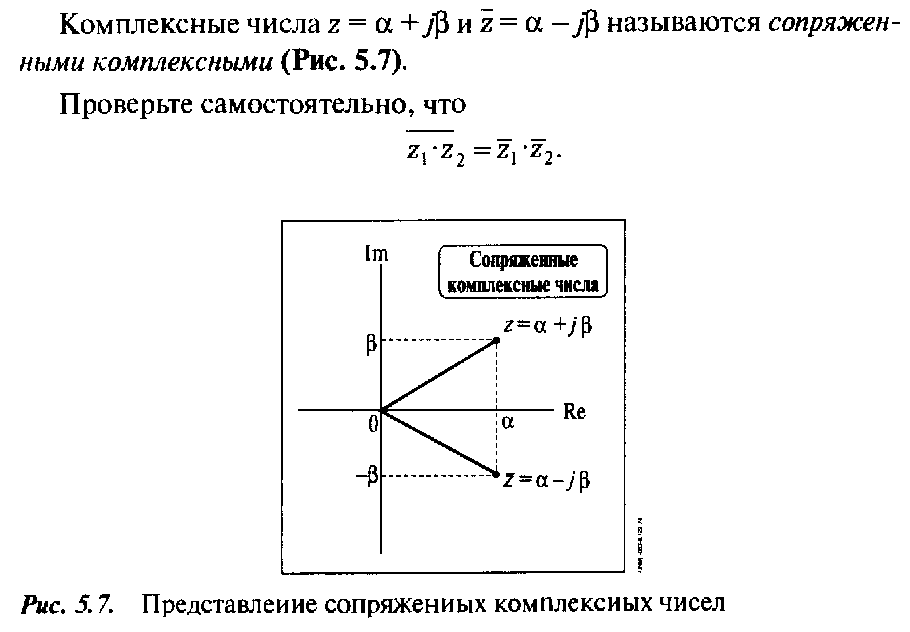
Якщо система функцій приймає комплексні значення, то умова ортогональності функцій має вигляд Функція є комплексно-спряженою до функції .

Довідка [6]

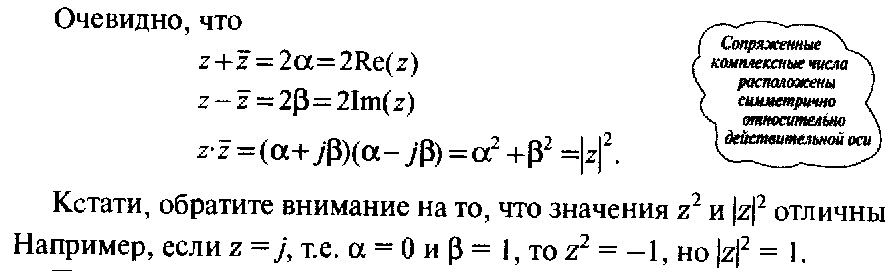
При застосуванні повної ортонормованої послідовності (базису) функцій енергія сигналу (тотожність Парсеваля), у разі ж тільки їх ортогональності (рівність Парсеваля), де , а потужність сигналу . Два співідношення для Е відомі як теорема Парсеваля.

Як вже йшлося на минулій лекції, вибір системи базисних функцій у складі апроксимуючого поліному визначається вимогами забезпечення простоти технічної реалізації апаратних (програмних) засобів дискретизації і відновлення сигналу. Доведено [2], що узагальнений ряд Фур’є при заданій системі функцій і фіксованій кількості доданків ряду забезпечує найкращу апроксимацію (у розумінні мінімума середньоквадратичної похибки) даної функції , тобто

досягає мінімуму, коли , при цьому є вірною нерівність Бесселя

,

тобто енергія (потужність) сигналу, який апроксимується лінійною комбінацією ортогональних базисних функцій, завжди є не меншою за енергію (потужність) апроксимуючої функції.

Дуже поширеним на практиці як при аналоговій, так і при цифровій обробці сигналів є застосування ортогонального базису, який утворений гармонічними функціями з кратними частотами. Такий базис забезпечує точне розкладання сигналу і, крім цього, гармонічне коливання (функція часу) – єдине, що зберігає свою форму при проходженні через лінійні кола з постійними параметрами.

Розкладанню в ряд Фур'є піддаються періодичні сигнали. При цьому вони представляються у вигляді суми гармонічних функцій або комплексних експонент з частотами, що утворюють арифметичну прогресію. Для того, щоб таке розкладання існувало, фрагмент сигналу тривалістю в один період повинен задовольняти умовам Дирихле:

• не повинно бути розривів другого роду (з гілками функції, що йдуть в нескінченність);

• число розривів першого роду (стрибків) має бути кінцевим;

• число екстремумів має бути кінцевим (рис. 3.1).

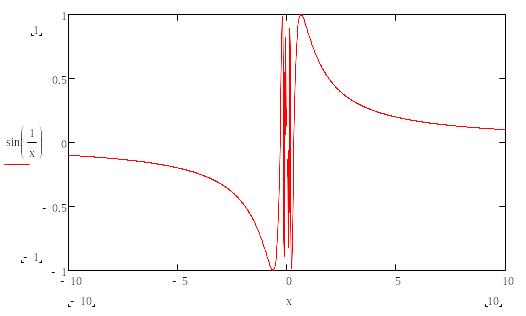
Рис. 3.1. Приклад функції, яка на кінцевому інтервалі має нескінченне число екстремумів в околиці нуля

Зауваження: Ряд Фур'є може бути застосований для представлення не лише періодичних сигналів, але і сигналів кінцевої тривалості. При цьому обумовлюється часовий інтервал, для якого будується ряд Фур'є, а в інші моменти часу сигнал вважається рівним нулю. Для розрахунку коефіцієнтів ряду такий підхід фактично означає періодичне продовження сигналу за межами даного інтервалу.

Залежно від конкретної форми базисних функцій розрізняють декілька форм запису ряду Фур'є.

Перший випадок – це синусно-косинусна форма.

Системою ортонормованих базисних функцій на інтервалі періоду сигналу у цьому випадку є , , , , , , ,..., де .

В цьому варіанті ряд Фур'є має наступний вигляд:

. (2)

Гармонічне коливання з індексом і ω_i=iω₁ називається i-ою гармонікою сигналу. Коефіцієнти ряду і розраховуються по формулах

, і .

Таким чином, у загальному випадку періодичний сигнал має постійну складову і нескінченний набір гармонік з частотами ω_i=iω₁ (i=1, 2, …).

Константа a₀ розраховується по загальній формулі для a_i. Заради цієї спільності і введена дещо дивна на перший погляд форма запису постійного доданку (з діленням на два). Цей доданок є середнім значенням сигналу на періоді:

.

Зауваження: Межі інтегрування не обов'язково мають бути такими, як в приведених вище формулах (від -T/2 до Т/2). Інтегрування може виконуватись по будь-якому інтервалу завдовжки Т - результат від цього не зміниться. Конкретні межі вибираються з міркувань зручності обчислень, наприклад, може виявитися зручніше виконувати інтегрування від 0 до Т або від -Т до 0.

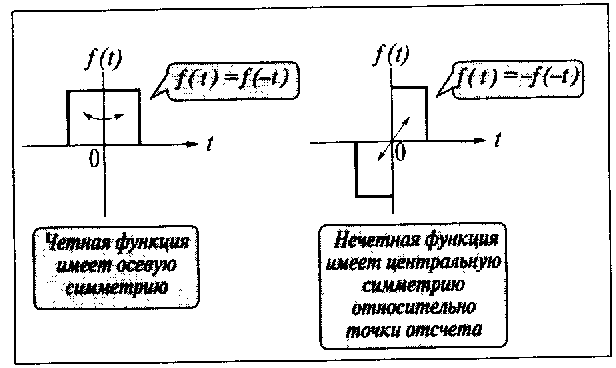
Якщо s(t) є парною функцією, то усі b_і дорівнюватимуть нулю і у формулі ряду Фур'є будуть присутні тільки косинусні доданки. Якщо s(t) є непарною функцією, дорівнювати нулю будуть, навпаки, косинусні коефіцієнти a_і і у формулі залишаться лише синусні доданки.

Другий випадок – дійсна форма

Деяка незручність синусно-косинусної форми ряду Фур'є полягає в тому, що для кожного значення індексу підсумовування i (тобто для кожної гармоніки з частотою ω_i=iω₁ у формулі фігурують два доданки - синусний і косинусний. Скориставшись формулами тригонометричних перетворень, суму цих двох доданків можна трансформувати в косинус тієї ж частоти з іншою амплітудою і деякою початковою фазою :

.

Довідка. , де

, .

Якщо s(t) є парною функцією, фази можуть набувати тільки значень 0 і π, а якщо s(t) - функція непарна, то можливі значення для фази рівні ±π/2.

Третій випадок – комплексна форма

Ця форма представлення ряду Фур'є є, мабуть, найбільш вживаною в радіотехніці. Вона виходить з речової форми представлення косинуса у вигляді напівсуми комплексних експонент cos x = (e^jx + e^-jx)/2, sin x = (e^jx -

- e^-jx)/2j (таке представлення витікає з формули Ейлера е^jх = cos x+j sin х).

Застосувавши це перетворення до дійсної форми ряду Фур'є, отримаємо суми комплексних експонент з додатними і від’ємними показниками степені

Далі трактуватимемо експоненти зі знаком "мінус" в показнику як члени ряду з від’ємними номерами. У рамках цього ж загального підходу постійний доданок а₀/2 стане членом ряду з нульовим номером. В результаті матимемо комплексну форму запису ряду Фур'є (зворотне перетворення Фур'є)

Система ортонормованих базисних функцій має вигляд , що можна безпосередньо перевірити

Комплексні коефіцієнти ряду пов'язані з амплітудами A_і і фазами , які є в дійсній формі запису ряду Фур'є, наступними співвідношеннями:

, , .

Нескладно виглядають і формули зв'язку з коефіцієнтами а_і і b_i синусно-косинусної форми ряду Фур'є, оскільки та :

; ; .

Звідси отримаємо формулу для безпосереднього розрахунку коефіцієнтів ряду Фур'є в комплексній формі (пряме перетворення Фур’є)

° .

оскільки е^-jх = cos x - j sin х.

Якщо s(t) є парною функцією, коефіцієнти ряду будуть дійсними, а якщо s(t) - функція непарна, коефіцієнти ряду виявляться чисто уявними.

Сукупність амплітуд гармонік ряду Фур'є часто називають амплітудним спектром, а сукупність їх фаз - фазовим спектром. Ці поняття не слід плутати з амплитудно- і фазочастотными характеристиками, які відносяться не до сигналів, а до ланцюгів.

Якщо аналізований сигнал s(t) є дійсним, то його амплітудний і фазовий спектри мають симетрію: , , .

Згідно до теореми Парсеваля

,

якщо інтеграл у лівій частині рівняння існує.

На кожному відкритому проміжку, на якому і кусочно-неперервні у точці розриву функції ряд Фур'є сходиться до напівсуми правої і лівої границь

,

де s(t) - початковий сигнал, s'(t) - сума ряду Фур'є для нього.