Лекція 2

Тема 2. Типи сигналів та їх кількісні параметри

Типи сигналів. Аналоговий сигнал. Дискретний сигнал. Цифровий сигнал. Перетворення типу сигналів. Графічне відображення сигналів. Тестові сигнали. Дельта-функція. Функція одиничного стрибка. Енергія і потужність сигналу.

1 Типи сигналів. Аналоговий сигнал. Дискретний сигнал. Цифровий сигнал. Перетворення типу сигналів. Енергія і потужність сигналу.

На минулій лекції ми розглянули класифікацію сигналів та математичні моделі деяких сигналів.

Аналогові сигнали - це сигнали, що описуються неперервною або кусково-неперервною функцією y_a(t), причому як ця функція, так і її аргумент t можуть набувати будь-яких значень на заданих інтервалах y (y_min, y_max) і t (t_min, t_max). Термін «аналоговий сигнал» підкреслює, що такий сигнал «аналогічний», тобто повністю подібний фізичному процесу, який його породжує. Одномірний аналоговий сигнал наочно представляється графіком (осцилограмою), що може бути неперервним або з точками розриву [5] (рис. 1.3, а - сигнал неперервний у часі та за значенням).

Дискретні сигнали - це сигнали, що змінюються дискретно у часі або за рівнем. У першому випадку він може набувати у дискретні моменти часу nT, де число T = const - інтервал (період) дискретизації; n = 0; 1; 2, ... - ціле число будь-яких значень y_a (y_min, y_max), які називають вибірками або відліками (рис. 1.3, б). У другому випадку значення сигналу y_a(t) існують у будь-який момент t (t_min, t_max), однак вони можуть набувати обмежений ряд значень h_i = ig, кратних кванту g.

Цифрові сигнали - квантовані за рівнем і дискретні за часом сигнали Y(nТ), які описуються квантованими решітчастими функціями (квантовани-ми послідовностями), які набувають у дискретні моменти часу пТ лише скін­ченний ряд дискретних значень - рівнів квантування h₁, h₂, ..., h_n (рис. 1.3, в -сигнал неперервний у часі та квантований за значенням, рис. 1.3, г - сигнал дискретизований у часі та квантований за значенням) описуються решітчастими функціями.

За характером зміни у часі сигнали поділяють на постійні, значення яких з часом не змінюються, і змінні, значення яких змінюються з часом. Постійні сигнали є найпростішим видом ВС. Змінні сигнали можуть бути безперервними за часом та імпульсними.

Рис.1.3.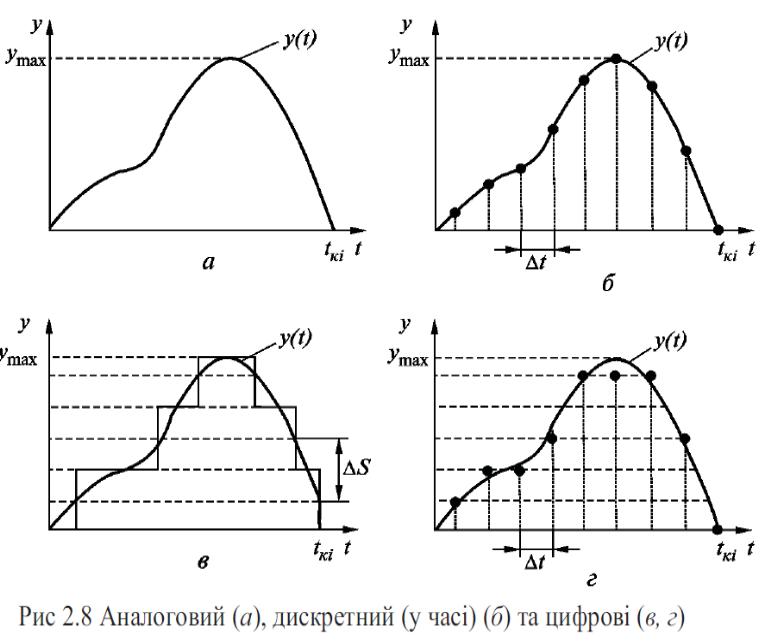

Перетворення типу сигналів. Узагальнена структурна схема системи цифрової обробки сигналів (ЦОС) приведена на рис. 2.1.

Часова дискретизація аналогового сигналу і його квантування по рівню виконується в аналого-цифровому перетворювачі АЦП. Вихідним сигналом АЦП є послідовність чисел, що поступає в процесор цифрової обробки сигналів ПЦОС, що виконує необхідну обробку. Процесор здійснює різні математичні операції над вхідними відліками; раніше отримані відліки і проміжні результати зберігаються в пам’яті процесора для використання в наступних обчисленнях. Відліки вихідного сигналу можуть бути використані для отримання аналогового вихідного сигналу за допомогою цифро-аналогового перетворювача ЦАП і (при необхідності) згладжувального фільтру Ф.

За допомогою ЦОС можуть бути здійснені усі відомі операції над сигналами. Наприклад, на основі цифрової обробки сигналів в метрології, радіотехніці і техніці зв'язку вирішуються наступні завдання: генерація, модуляція, формування і корекція сигналів, фільтрація і оцінювання, аналіз спектрів, виявлення і розпізнавання сигналів, кодування і декодування, обробка зображень тощо.

Принципові переваги ЦОС :

• багатофункціональність обробки, тобто можливість використання одного і того ж процесора для виконання різних операцій обробки шляхом зміни програми;

• мультиплексування, тобто можливість обробки сигналів від декількох датчиків в проміжках між суміжними тактами, що особливо актуально при реалізації багатоканальних інформаційно-вимірювальних систем;

• відсутність принципових обмежень на складність обробки (принципово можливо забезпечити необхідну точність обробки при будь-якої складності алгоритмах);

• зняття обмежень на види обробки, властиві аналоговій техніці, і можливість реалізації будь-яких формально описуваних перетворень.

Теорія ЦОС вивчає принципи і методи побудови алгоритмів, програм і технічних засобів цифрової обробки сигналів. Залежно від засобів реалізації (апаратні, програмні або змішані) розглядаються завдання розробки і реалізації алгоритмів ЦОС, методи синтезу фізично можливих операторів для різноманітних прикладних завдань, процедури досягнення точності виконання алгоритмів.

Як програмний, так і апаратний способи реалізації ЦОС базуються або на часовому, або на спектральному підході. Часовий підхід за своєю суттю є більш "фізичним", він нагадує фізичний процес обробки сигналів в аналоговій системі. У зв'язку з цим розглянемо спочатку принципи часового підходу.

Постановка завдання дискретизації

Представлення неперервного сигналу на інтервалі сукупністю відліків (координат) може бути записане у вигляді

(1)

де - оператор дискретного представлення сигналу, що реалізовується пристроєм, званим дискретизатором. Аналогічно можна записати операцію відновлення функції , так званою відтворюючою функцією, по сукупності відліків

(2)

де - оператор відновлення, що реалізовується пристроєм відновлення сигналу. Очевидно, відтворююча функція відображує початковий сигнал з деякою поточною похибкою наближення (відновлення): Завдання дискретизації в математичному плані зводиться до спільного вибору пари операторів і , що забезпечують задану точність відновлення сигналу.

У загальному випадку відтворююча функція може бути представлена апроксимуючим поліномом

, (3)

де система базисних функцій. Передбачається, що базисні функції ортогональні (тобто скалярний добуток ортонормованих базисних функцій , c=const, для ортонормованих базисних функцій – c=1) і забезпечують збіжність ряду до функції при що дає можливість обмежити число відліків (координат) відповідно до заданої похибки відновлення.

Основні завдання, що вирішуються при дискретизації сигналу:

• вибір кроку дискретизації при заданій похибці дискретизації (наближення, відновлення);

• оцінка істотності відліків, що забезпечують представлення початкового сигналу із заданою точністю, і усунення можливої надмірності.

Алгоритм рішення задачі дискретизації:

• по наявних відліках, використовуючи базисні ортогональні функції і методи інтерполяції або екстраполяції, будують з тією або іншою мірою наближення початковий сигнал, тобто отримують відтворюючу функцію ;

• оцінюють ефективність дискретизації при вибраному методі апроксимації, визначаючи похибку дискретизації (відновлення) із заданим кроком дискретизації або крок дискретизації при заданій похибці.

Вибір системи базисних функцій у складі апроксимуючого полінома (см (3)) визначається вимогою забезпечення простоти технічної реалізації апаратних (програмних) засобів дискретизації і відновлення сигналу. При неортогональних представленнях сигналу часто застосовують степеневі алгебраїчні поліноми виду

(4)

де дійсні коефіцієнти.

Як ортогональні базисні функції використовують функції відліків (ряд Котельникова), поліноми Лежандра, функції Уолша й інші. Якщо базисні функції вибрані так, що значення апроксимуючого полінома співпадають зі значеннями вибірки початкового сигналу в моменти їх відліку, то такий поліном називають інтерполяційним (Інтерполяція — в обчислювальній математиці спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень. Інтерполяцією називають такий різновид апроксимації, при якій крива побудованої функції проходить точно через наявні точки даних [http://uk.wikipedia.org/wiki/Інтерполяція].). З точки зору скорочення числа відліків інтерполяційні методи відновлення сигналу прийнятніші, проте для їх реалізації потрібна затримка сигналу на інтервал інтерполяції, що у ряді випадків неприпустимо. Наприклад, у системах управління, що працюють в реальному часі, використовують екстраполяційні методи, що не вимагають затримки сигналу при проведенні операцій визначення значень вибірок і відновлення сигналу (Экстраполя́ция, экстраполи́рование (от лат. extrā — вне, снаружи, за, кроме и лат. polire — приглаживаю, выправляю, изменяю, меняю) — особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями. Иначе, экстраполяция — приближённое определение значений функции в точках, лежащих вне отрезка, по её значениям в точках внутри отрезка [http://ru.wikipedia.org/wiki/Экстраполяция]).

При обраному способі побудови відтворюючої функції повинна забезпечуватися задана точність відновлення сигналу. Залежно від цільового призначення отримуваної інформації використовують різні критерії точності наближення до що визначають чисельні значення похибки відновлення і, отже, дискретизації.

Критерії оцінки точності відновлення (похибки дискретизації):

1. Відповідно до критерію найбільшого відхилення встановлюється максимальне значення допустимої похибки відновлення

(5)

де поточна похибка відновлення; ділянка апроксимації.

2. При використанні критерію середньоквадратичного наближення задається значення допустимої середньоквадратичної похибки відновлення

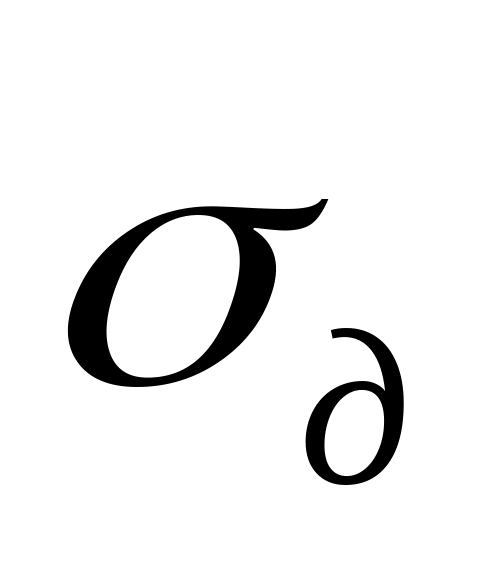
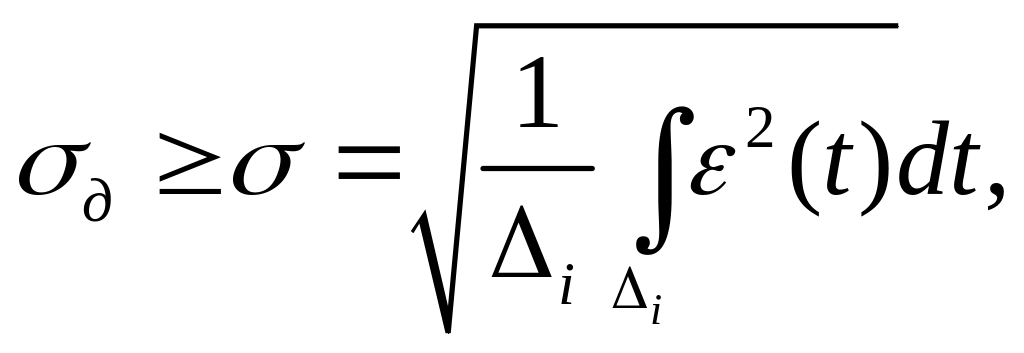(6)

де середньоквадратична похибка наближення. Зазвичай цей критерій використовується для функцій, інтегрованих в квадраті.

3. Інтегральний критерій наближення визначається співвідношенням:

(7)

де допустима середня похибка наближення; ε - середня похибка наближення.

4. Імовірнісний критерій визначає допустиму ймовірність того, що поточна похибка наближення не перевищить деякого певного значення

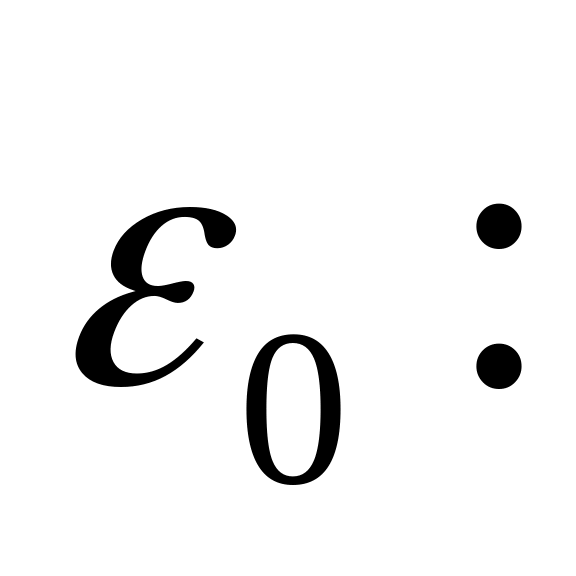
(8)

Важливою ознакою процесу дискретизації є регулярність відліків. Якщо крок дискретизації постійний в усьому діапазоні перетворення, дискретизація вважається рівномірною. Методи рівномірної дискретизації застосовуються найширше. Проте невідповідність кроку дискретизації характеру поведінки конкретної реалізації досліджуваного процесу на окремих ділянках часто призводить до значної надмірності відліків.

Якщо крок дискретизації змінюється, наприклад, залежно від швидкості зміни сигналу або за заданою програмою, дискретизацію називають нерівномірною. Розрізняють адаптивні методи нерівномірної дискретизації, при яких крок змінюється залежно від поточної зміни параметрів сигналу, і програмовані методи, в яких зміна кроку дискретизації виробляється оператором на основі аналізу інформації, що поступає, або відповідно до заздалегідь встановленої програми. Адаптивні методи нерівномірної дискретизації забезпечують ефективне усунення надмірності у відліках сигналів. Інтервал дискретизації в цьому випадку тісно пов'язаний з поточними значеннями параметрів реалізації сигналу.