24. Неперервність елементарних функцій.

Розглянемо питання про неперервність елементарних функцій. Як ми знаємо, це функції, які утворено з основних елементарних функцій за допомогою скінченного числа арифметичних дій та операцій суперпозиції. Отже, якщо ми доведемо, що всі основні елементарні функції неперервні в своїй області визначення, то тим самим доведемо, що елементарні функції також неперервні в своїй області визначення.

1. Степенева функція з натуральним показником. Функція неперервна на , оскільки при для будь якого . Тому функція неперервна на як добуток скінченного числа неперервних функцій. Оскільки функція , де – стала, неперервна на ( ), то функція , де , також неперервна на , а звідси випливатиме, що многочлен степеня

є неперервною на функцією (як сума скінченного числа неперервних функцій).

Раціональна функція

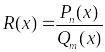, де – многочлени степеня і відповідно, неперервна як частка двох неперервних функцій в усіх точках множини , які не є коренями многочлена . Тобто в усіх точках, де функція визначена.

2. Степенева функція з раціональним показником. Розглянемо функцію , де . Якщо , і непарне, то функція неперервна та зростаюча на , отже має обернену функцію , яка також неперервна та зростаюча на . Нехай тепер , і парне. Розглянемо «звужену» функцію , яку визначено лише на множині . Тоді така функція має обернену функцію , яка визначена і неперервна на множині .

Функція , , також має обернену – це функція .

Розглянемо тепер степеневу функцію з цілим від’ємним показником, тобто функцію , . Вона визначена і неперервна на множині . При ( ) ця функція оборотна на множині , а при ( ) оборотна на множинах та .

Нехай тепер , де . За означенням:

, .

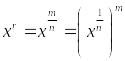Функція неперервна і зростаюча на . Функція неперервна на , зростаюча при і спадна при . Тому функція неперервна на , зростаюча, якщо і спадна, якщо .

Враховуючи неперервність раціональних функцій в їх області визначення, тепер можна стверджувати, що ірраціональні функції також неперервні в їх області визначення. Отже алгебраїчні функції неперервні в їх області визначення.

3. Тригонометричні та обернені тригонометричні функції.

Лема. Для виконано:

. (24.1)

Доведення. Доведемо це співвідношення спочатку для . Виконаємо наступну геометричну побудову (рис. 48).

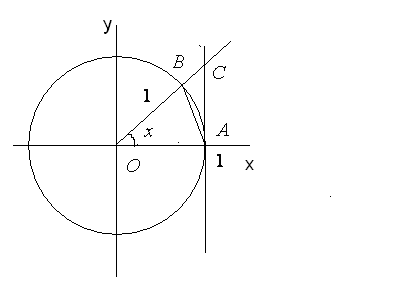
Рис. 48.

Побудуємо коло з центром у початку координат і радіусом 1. Проведемо радіус цього кола під кутом ( в радіанах) до додатного напряму осі абсцис, причому продовжимо його за коло.

Через точку проведемо пряму, перпендикулярну осі абсцис (дотичну до кола). Точку перетину цієї прямої і продовження радіусу позначимо через . Тоді площа трикутника буде дорівнювати , площа сектора дорівнює , а площа трикутника дорівнює . Очевидна подвійна нерівність:

.

Або:

, тобто

.

Оскільки тут , то поділивши на , матимемо:

.

Або:

.

Оскільки функції та парні, то співвідношення (24.1) виконано й для .

Лема. виконано:

. (24.2)

Доведення. Якщо , то нерівність (24.2) виконано. Нехай . Якщо , то з (24.1) маємо:

, з чого одразу випливає (24.2). Оскільки функція парна, то нерівність (24.2) виконується при . А якщо , то також виконується, оскільки і .

Теорема. Функції , неперервні на .

Доведення. Нехай . Надамо значенню приріст і розглянемо відповідний приріст функції :

.

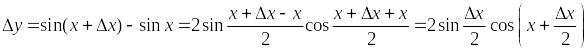Звідси і з нерівності (24.2) маємо:

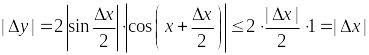, отже при , тобто функція неперервна в точці , а внаслідок довільності це означає, що функція неперервна на всій числовій прямій.

Функція неперервна на як суперпозиція двох неперервних функцій: .

Теорему доведено.

Наслідок 1. Функція неперервна на множині , а функція неперервна на множині .

Дійсно, функція неперервна як частка двох неперервних функцій в усіх точках множини , крім тих, де функція дорівнює нулю, а саме . Функція неперервна в усіх точках множини , крім тих, де функція дорівнює нулю, а саме .

Наслідок 2. Функція , неперервна як обернена до функції на відрізку (див. п. 16). Функція , неперервна як обернена до функції на відрізку . Функція неперервна на як обернена до функції на інтервалі . Функція неперервна на як обернена до функції на інтервалі .

4. Показникова та логарифмічна функції. Доведемо, що функція неперервна на . Розглянемо спочатку випадок . Нехай . Надамо значенню приріст і розглянемо:

.

Якщо ми доведемо, що , то виконуватиметься , тобто функція неперервна .

Скористаємось рівністю (див. п.10, приклад 2):

.

Звідси випливає, що й

.

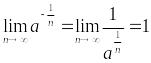А тоді таке, що

.

Якщо тепер , тобто , то, оскільки при функція зростаюча, матимемо:

, звідки

,

або

, звідки внаслідок довільності випливає, що .

Отже, внаслідок довільності , функція при неперервна на .

Нехай тепер . Тоді , і

.

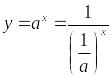Оскільки функція за доведеним вище неперервна, і , то функція неперервна на як частка двох неперервних функцій.

Функція при неперервна на як обернена до неперервної та зростаючої функції , а при – неперервна на як обернена до неперервної та спадної функції .

Таким чином ми довели, що всі основні елементарні функції неперервні в їх області визначення. Звідси випливає твердження.

Всі елементарні функції неперервні в їх області визначення.