16. Операції над функціями. Складена та обернена функції.

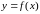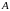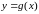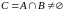Визначимо тепер операції над функціями. Нехай маємо функцію , яка визначена на множині , і функцію , яка визначена на множині . Припустимо, що . Тоді на множині можна визначити суму функцій . Значення цієї функції у кожній точці дорівнює сумі . Аналогічно на множині можна визначити різницю , добуток та частку цих функцій (останню крім точок, де ).

Нехай на множині визначено функцію , множиною значень якої є множина . І нехай на множині визначено функцію , множиною значень якої є множина . Припустимо, що . Тоді на деякій підмножині множини визначено так звану складену функцію , множиною значень якої є деяка підмножина множини . Тобто складена функція утворюється шляхом підстановки значень одної функції замість аргументу іншої. Така операція називається операцією суперпозиції функцій і .

Щоб знайти – область визначення складеної функції , треба з’ясувати, для яких значень значення функції належать області визначення функції . Взагалі кажучи, це досить складна задача. Для її розв’язання, як правило, треба розв’язувати нерівності та системи нерівностей. Значна частина таких нерівностей розглядається у шкільному курсі алгебри.

Розглянемо приклад. Нехай задано функцію . Тут

. І функцію . Тут

. Тоді .

Утворимо за допомогою суперпозиції функцій і складену функцію:

.

Знайдемо її область визначення . Оскільки , то повинна виконуватись нерівність , звідки . Тобто . Множина значень складеної функції: .

Введемо тепер поняття оберненої функції. Розглянемо функцію , яку визначено на деякій множині 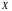, а множиною її значень є множина . Припустимо тепер, що для кожного значення 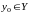існує єдине значення таке, що . Тобто двом різним значенням аргументу відповідають різні значення функції. Оскільки у свою чергу згідно з означенням функції існує єдине значення таке, що , то між елементами множин та встановлено взаємно однозначну відповідність. 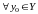Визначимо тепер на множині функцію наступним чином: : , де . Тобто фактично кожному значенню функції поставлено у відповідність відповідний аргумент цієї функції (він, згідно умови, визначається однозначно). Функція називається оберненою до функції . Якщ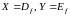о , то . Зрозуміло, що у свою чергу функція буде оберненою до функції . Щоб знайти обернену функцію для функції треба рівняння розв’язати відносно за умови, що такий розв’язок існує та єдиний.

Який вигляд має графік функції, оберненої до даної? Оскільки кожна точка кривої є водночас точкою кривої , то графік функції 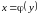співпадає з графіком функції . Тільки якщо у випадку за відомим значенням встановлюється значення (рис. 29 а), то у випадку за відомим встановлюється значення (рис. 29 б).

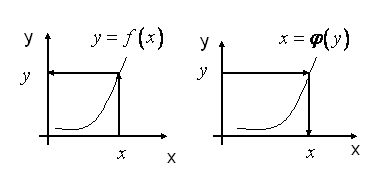
а б

Рис. 29.

Припустимо тепер, що у виразі змінні та змінені місцями, тобто розглянемо функцію . Тоді кожна точка кривої стане точкою кривої . Оскільки в системі координат точки і симетричні відносно прямої , то графіки взаємно обернених функцій також симетричні відносно цієї прямої, тобто бісектриси 1–го та 3–го координатних кутів (рис. 30).

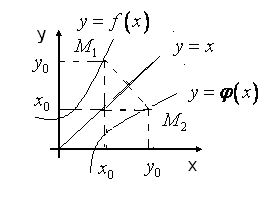
Рис. 30.

Приклади.

1. Розглянемо функцію . Тоді звідси: – обернена до неї. Змінюючи в цій рівності та місцями, отримаємо: . Зображуємо графіки функцій та в одній системі координат і переконуємось в тому, що вони симетричні відносно прямої (рис. 31).

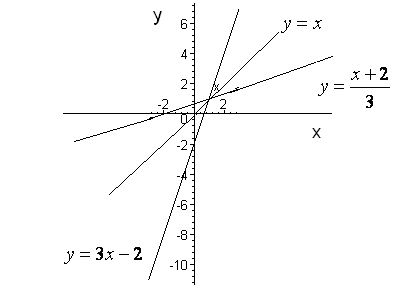
Рис. 31.

2. До функції оберненою є функція (тут вже змінили місцями та ). Для цієї функції (рис. 32).

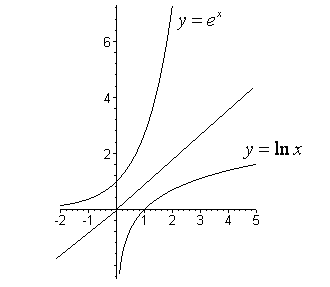
Рис. 32.

3. Побудуємо обернену до функції . Одразу це зробити неможливо, оскільки, як ми зауважили вище, одному й тому ж значенню функції відповідає безліч значень аргументу (внаслідок періодичності). Тому спочатку ми повинні звузити область визначення цієї функції. Власне розглянути іншу функцію, яку визначено лише на відрізку 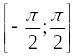, і на цьому відрізку її значення співпадають зі значеннями функції . Така функція має обернену функцію . Для неї 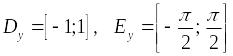(рис.33).

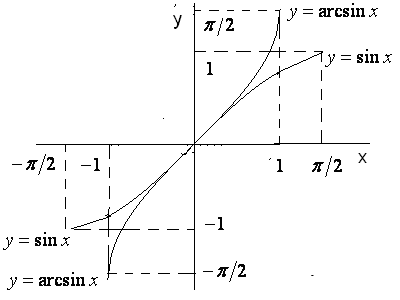
Рис. 33.

4. Існують функції, які є оберненими до самих себе. Виникає така ситуація тоді, коли розв’язок рівняння має вигляд . Наприклад, такими є функції , . Графіки таких функцій самі симетричні відносно прямої . На рис. 34 зображено графік функції .

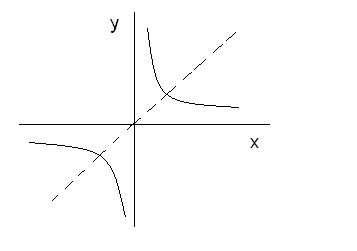
Рис. 34.