1.4.5. Определение главных размерений судна с использованием уравнения и.Г. Бубнова.

Уравнение И.Г. Бубнова – результат совместного решения уравнения весов и уравнения плавучести. Оно позволяет определить как приращения главных размерений – , , , так и приращения составляющих весовые нагрузки dPi в зависимости от изменения ряда независимых величин.

В основу этого уравнения положено

, (2.85)

т.е. приращение сил поддержания равно приращению весовой нагрузки. Тогда уравнение И.Г. Бубнова запишется в виде

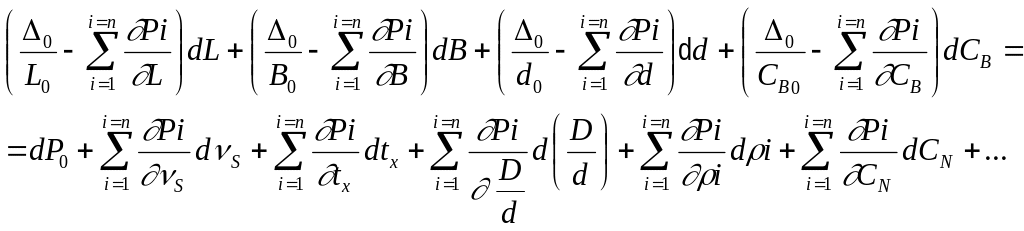, (2.86)

где , , , , – водоизмещение, главные размерения и коэффициент общей полноты прототипа.

Правая часть уравнения (2.86) – это приращения составляющих нагрузки масс при изменении величин:

независимых весов – ;

скорости хода – ;

автономности по топливу - ;

измерителей масс – ;

38

отношения – и т.д.

Для нахождения частных производных, входящих в уравнение (2.86), необходимо принять функциональные зависимости для каждой составляющей нагрузки масс. Для примера примем, с некоторой корректировкой, ранее используемые зависимости (см. дифференциальное уравнение масс).

, (2.87)

, (2.88)

, (2.89)

, (2.90)

, (2.91)

, (2.92)

Используя функциональные зависимости (2.87 − 2.92) получим

;

;

;

.

Обозначив правую часть уравнения (2.86) через и определим ее составляющие

;

;

39

;

Приращение относительной высоты борта определяется как разность между принятым соотношением и соотношением прототипа.

Для определения , , и недостаточно иметь только уравнение И.Б. Бубнова, поскольку неизвестных четыре, а уравнение одно. Поэтому к этому уравнению добавляются обоснованные ранее соотношения главных размерений – , коэффициент общей полноты – и получим систему

, (2.93)

Решив систему уравнений (2.93) относительно неизвестных , , и можно уже определить главные размерения проекта

, (2.94)

Уравнение И.Г. Бубнова рационально решать табличным способом. Пример такого решения – таблица 1.4.

Порядок работы с таблицей следующий. Приняв соответствующие функциональные зависимости (столбец 4), записываем нагрузку прототипа (столбец 3).

В столбцах 5, 6, 7, 8 вычисляются , , , и .