Лекция №1.

Электрическое поле

системы неподвижных зарядов в вакууме.

Электрический заряд. Закон Кулона. Напряжённость электростатического поля. Силовые линии. Принцип суперпозиции и его применение к расчёту поля системы неподвижных зарядов. Работа электростатического поля при перемещении зарядов. Циркуляция вектора напряжённости. Связь напряжённости и потенциала.

Электрический заряд Q или q - проявляется в силовом взаимодействии электрически заряженных тел.

Существует "элементарный заряд" - минимально возможный заряд . Любое тело может нести целое число элементарных зарядов. Заряды могут быть "положительными" и "отрицательными". В классической электродинамике имеет место закон сохранения электрического заряда: электрический заряд может переходить с одного тела на другое, но не может исчезнуть совсем без следа. Закон сохранения электрического заряда - Бенжамин. Франклин (времена великой французской революции).

Закон Кулона.

История - английские книги, итальянские, французские, русские...

Френсис Бэкон.

Генри Кавендиш.

Дж. Пристли

Шарль Огюстен Кулон. (1785 г.)

Понятие "точечный заряд". Понятие "вакуум". Понятие "центральная сила".

Школьный вариант: неподвижные точечные заряды в безграничном однородном пространстве (вакуум) взаимодействуют между собой с силой

:

Сила притяжения - заряды разного знака. Сила отталкивания - заряды одного знака. R - расстояние между зарядами, k - коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ величина заряда измеряется в "кулонах", расстояние - в метрах, , - 'электрическая постоянная". В системе СГСЕ - для величины заряда имеется "единица электрического заряда СГСЕ", расстояние измеряется в сантиметрах, величина k равна 1.

Вариант вуза: имеет место некоторая конкретная система координат (декартовая в простейшем случае). Положение точечного заряда определено радиус-вектором , положение точечного заряда определено радиус-вектором . Расстояние между зарядами равно модулю разности рассматриваемых радиус-векторов

Cила, которую испытывает второй заряд со стороны первого заряда, - вектор, определяемый зависимостью:

Следствие:

, ,

Легко проверить:

- модуль вектора силы, - направляющие косинусы рассматриваемого вектора силы.

Принцип суперпозиции. Если имеется некоторая система неподвижных точечных зарядов, если кроме этого имеется отдельный заряд, не включённый в рассматриваемую систему электрических зарядов, то каждый электрический заряд, содержащийся в системе зарядов, действует на выделенный заряд так, как будто остальных зарядов не существует. Сила такого взаимодействия определяется по закону Кулона. Если мы хотим определить результирующую силу действия всех (или части ) зарядов системы на выделенный заряд, то эта сила определяется как векторная сумма сил попарного взаимодействия выделенного заряда с каждым зарядом, входящем в систему зарядов.

Напомним, сложение векторных величин - правило треугольника или правило параллелограмма (геометрия), а в координатной форме записи имеем

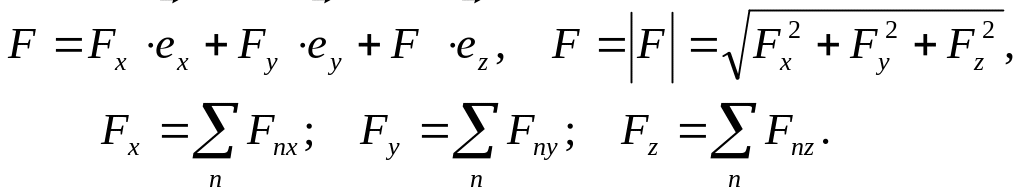
Напряжённость электростатического поля.

Понятие "поле". Если в каждой точке пространства определена скалярная функция Ф(x.y,z), говорят что имеется скалярное пол)Ф. Если в каждой точке пространства определена векторная функция , говорят что имеется векторное поле .

Если в каждой точке пространства (или в некоторой его части) рассматриваемый точечный электрический заряд испытывает электрическое воздействие, пропорциональное величине этого заряда, можно сказать, что в нашем пространстве существует векторное поле напряжённости электростатического поля. Определяется оно следующим соотношением:

Важно (и очень удобно), что напряжённость электростатического поля - вектор - не зависит от величины и знака электрического заряда, помещаемого в рассматриваемую точку пространства. В электростатике поле определяется совокупностью неподвижных электрических зарядов, внешних по отношению к электрическому заряду, испытывающему их воздействие.

Размерность напряжённости электростатического поля в системе СИ - Вольт на метр.

Поместим точечный электрический заряд в начало координат декартовой системы координат, а в точку пространства, описываемую радиус-вектором , -точечный электрический заряд q. В соответствии с законом Кулона запишем выражение для вектора силы, действующей на заряд q :

Можно сказать, что вектор напряжённости электростатического поля, созданного зарядом в точке наблюдения (точка пространства, где находится точечный электрический заряд q) равна

Если точечный заряд помещён в точку пространства с радиус-вектором , легко переписать предыдущее выражение:

Заметим, что координаты заряда, создающего электростатическое поле, играют в полученном соотношении роль параметров, независимыми переменными являются координаты точки наблюдения. Похожую роль играет и величина электрического заряда, создающего поле .

В электростатике электрические заряды создают поле напряжённости электрического поля. Можно сказать, что электрические заряды являются "источниками" элетрического поля.