1.13 Вимушені коливання. Диференційне рівняння вимушених коливань та його розв’язок
Вимушеними називаються коливання, що виникають у системі під дією періодичного зовнішнього фактору. Це може бути періодична сила, змінна напруга і т.ін.
Нехай
на пружинний маятник діє періодична
сила, яка змінюється по гармонічному
закону з циклічною частотою Ω
.
Запишемо другий закон Ньютона
.
Після спрощень, одержимо
.
Позначивши
,
одержимо диференційне рівняння вимушених
коливань пружинного маятника
.
В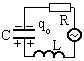
коливальний контур увімкнено джерело
змінної напруги
з циклічною частотою Ω. Записуємо другий
закон Кірхгофа
.
.
Позначивши
,
одержимо диференційне рівняння вимушених електричних коливань
(1.56)
Видно,
що обидва рівняння ідентичні. Будемо
розв’язувати рівняння електричних
коливань. У відповідності з §1.2
.
Тут
рівняння (1.54) незатухаючих власних
коливань,
часткове рішення неоднорідного рівняння
(1.56). Згідно із зауваженням §1.2 переведемо
праву частину рівняння (1.56) в показову
форму
,
додавши до неї вираз
.
Одержуємо нове рівняння
. (1.56*)
Частковий
розв’язок цього рівняння має вид
. Константу
інтегрування А знайдемо, підставивши
цей вираз в (1.56*) .
.
Після
скорочення на
знайдемо
.
Тут комплексне число у знаменнику
переведене із алгебраїчної форми в
показову.
Модуль
цього числа
(1.57),
його
аргумент 
.
(1.58)
Таким
чином
.
Знайдемо
шляхом виділення із
дійсної частини, так як права частина
рівняння (1.56) дійсне число. Отже
.
Загальний розв’язок рівняння (1.56) вимушених коливань
(1.59)
складається
із двох гармонічних функцій: перша із
частотою ω власних затухаючих коливань
і амплітудою, яка зменшується з часом
по експоненті; друга із частотою Ω
зовнішнього фактору, амплітудою та
початковою фазою, які не залежать від
часу, але залежать від частоти Ω
(див.(1.57), (1.58)). Через час приблизно
амплітуда першого доданку в (1.59) практично
зникає. Наступає сталий режим вимушених
коливань
. (1.60)