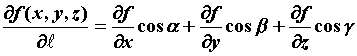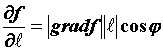1.Справочный материал.
Производная неявной функции.
|
|
Производная по направлению
|
где
|
Градиент.
|
|
.
,
.
-
направляющие косинусы вектора
.
2. Задания для самостоятельной работы.
Задание1. Дана функция Z=f(x,y). Найти частные производные 1 и 2 порядка.
1.1. |
|
1.2. |
|
1.3. |
|
1.4. |
|
1.5. |
|
1.6. |
|
1.7. |
|
1.8. |
|
1.1. |
|
1.10. |
|
1.11. |
|
1.12. |
|
1.13. |
|
1.14. |
|
1.15. |
|
1.16. |
|
1.17. |
|
1.18. |
|
1.19. |
|
1.20. |
|
Задание 2. Найти наибольшее и наименьшее значение функции в замкнутой области Д.
2.1. |
Z = |
|
|
2.2. |
Z = |
|
|
2.3. |
Z = |
|
|
2.4. |
Z = |
|
|
2.5. |
Z = |
|
|
2.6. |
Z = |
|
|
2.7. |
Z = |
|
|
2.8. |
Z = |
|
|
2.9. |
Z = |
|
|
2.2. |
Z = |
|
|
2.11. |
Z = |
|
|
2.12. |
Z = |
|
|
2.13. |
Z = |
|
|
2.14. |
Z = |
|
|
2.15. |
Z = |
|
|
2.16. |
Z = |
|
|
2.17. |
Z = |
|
|
2.18. |
Z = |
|
|
2.19. |
Z = |
|
|
2.20. |
Z = |
|
|
,
,
Задание 3. Даны функция Z=Z(x,y), точка А(х0,у0) и вектор . Найти:
grad Z в точке А;
производную в точке А по направлению вектора .
3.1. |
Z = |
|
А(1,1), |
= |
|
3.2. |
Z = |
|
А(2,1), |
= |
|
3.3. |
Z = |
|
А(1,1), |
= |
|
3.4. |
Z = |
|
А(1,1), |
= |
|
3.5. |
Z = |
|
А(2,1), |
= |
|
3.6. |
Z = |
|
А(2,3), |
= |
|
3.7. |
Z = |
|
А(1,2), |
= |
|
3.8. |
Z = |
|
А(1,3), |
= |
|
3.9. |
Z = |
|
А(-1,2), |
= |
|
3.2. |
Z = |
|
А(1,1), |
= |
|
3.3. |
Z = |
|
А(1,1), |
= |
|
3.12. |
Z = |
|
А(2,3), |
= |
|
3.13. |
Z = |
|
А(2,1), |
= |
|
3.14. |
Z = |
|
А(3,2), |
= |
|
3.15. |
Z = |
|
А(1,1), |
= |
|
3.16. |
Z = |
|
А(1,3), |
= |
|
3.17. |
Z = |
|
А(1,4), |
= |
|
3.18. |
Z = |
|
А(1,1), |
= |
|
3.19. |
Z = |
|
А(2,1), |
= |
|
3.20. |
Z = |
|
А(2,2), |
= |
|
,
Задание 4. Изменить порядок интегрирования.
1.1
.
1.2
.
1.3
.
1.4
.
1.5
.
1.6
.
1.7
.
1.8.
.
1.9
.
1.10
.
1.11
.
1.12
.
1.13
.
1.14
.
1.15
.
1.16
.
1.17
.
1.18
.
1.19
.
1.20
.
Задание 5. Вычислить двойной интеграл.
2.1
.
2.2
.
2.3
.
2.4
.
2.5
.
2.6
.
2.7
.
2.8
.
2.9
.
2.10
.
2.11
.
2.12
.
2.13
.
2.14
.
2.16
.
2.17
.
2.18
.
2.19
.
2.20
.
Задание 6. Найти площадь фигуры, ограниченной данными линиями.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
Зачетное задание №4 Интегралы
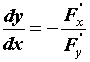
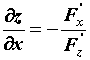
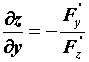