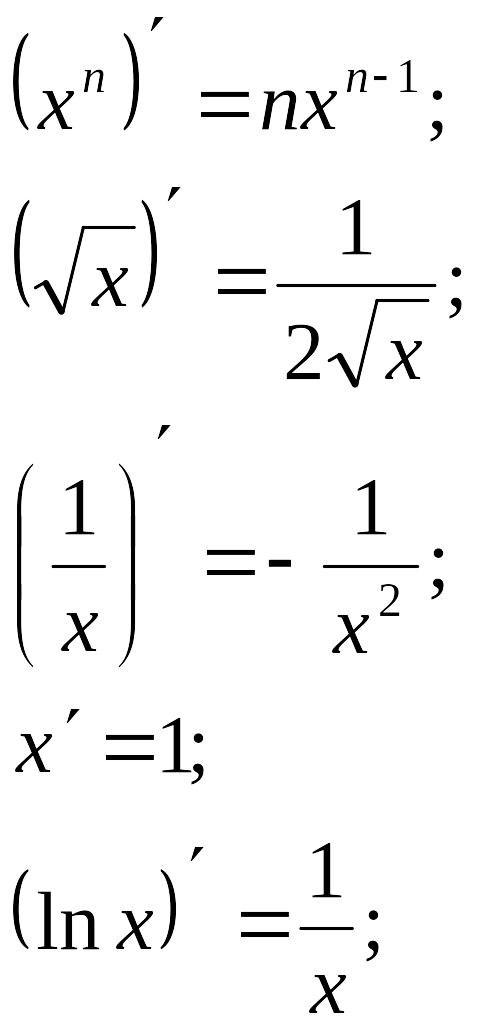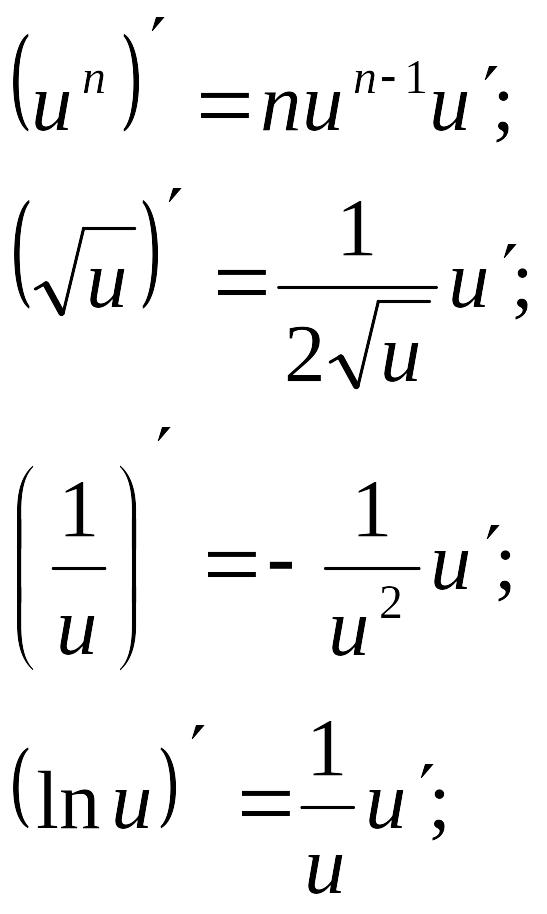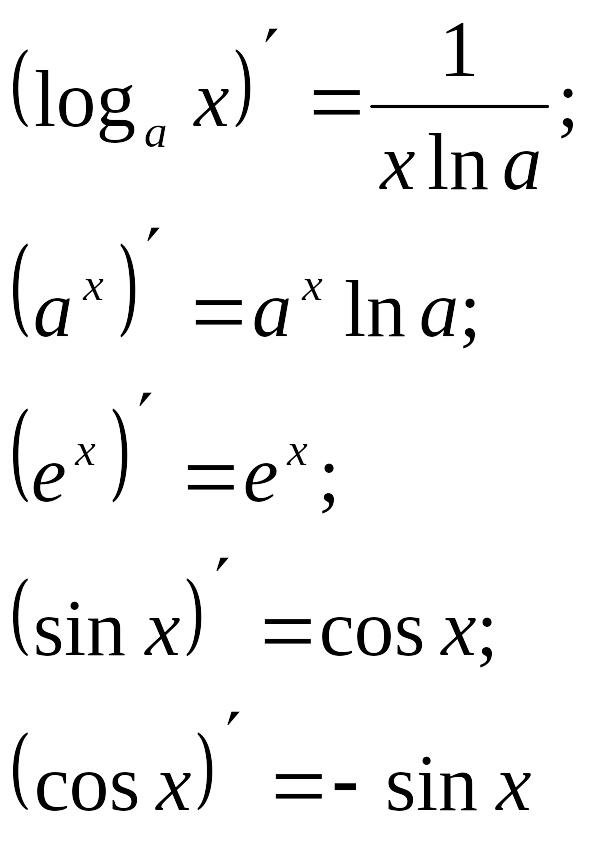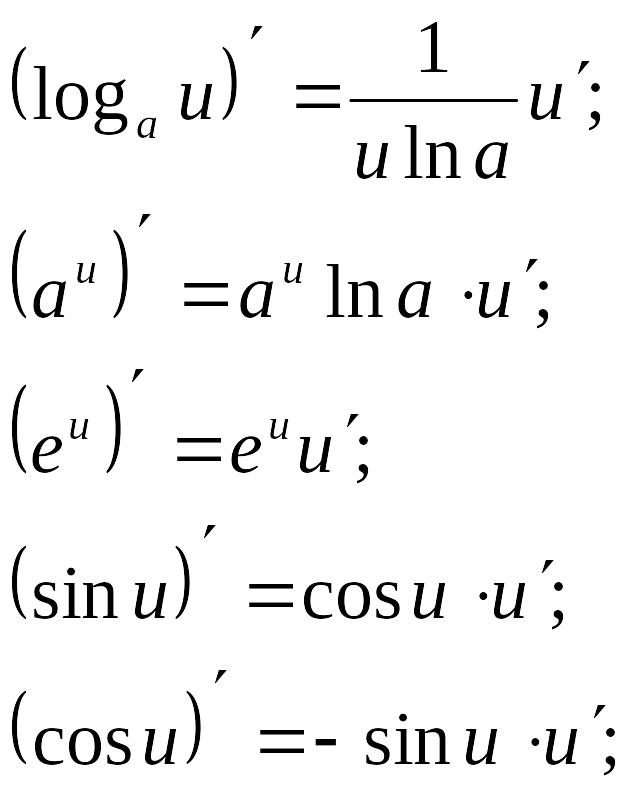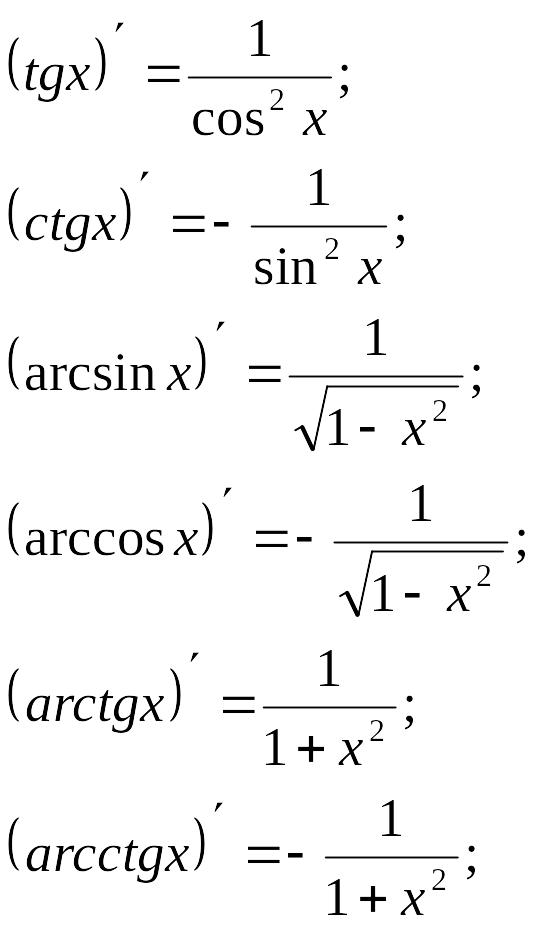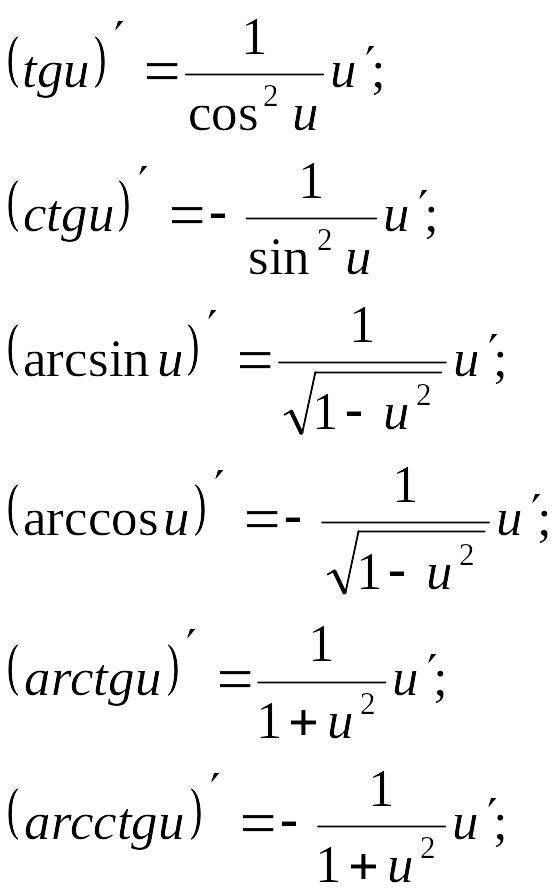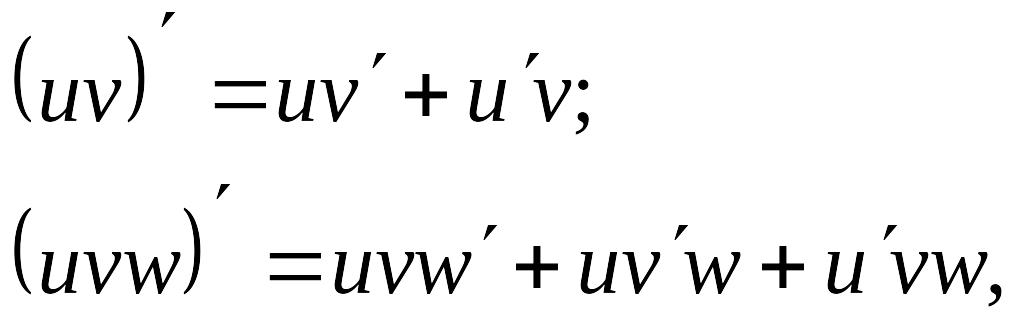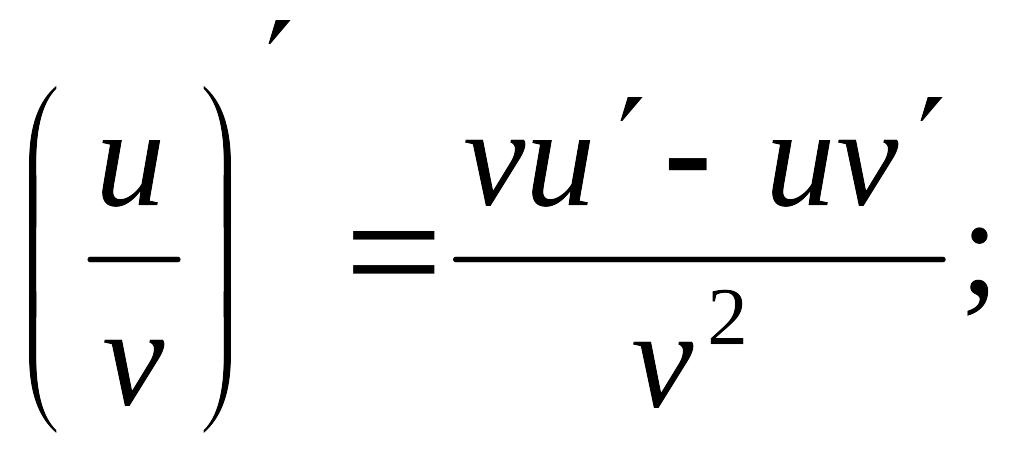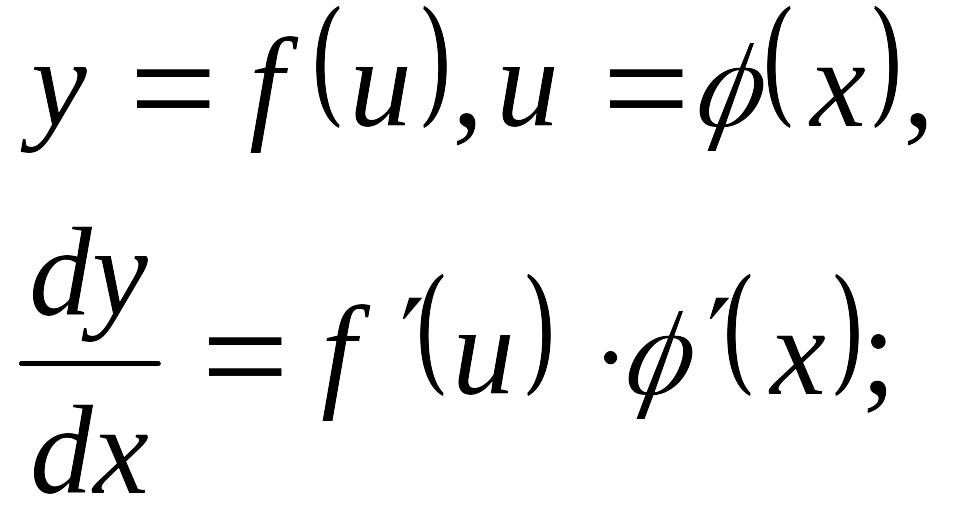1. Справочный материал.

Производной функции в фиксированной точке x называется предел при выражения при условии, что этот предел существует.

Обозначения: .

Таблица производных основных элементарных функций

Производные основных элементарных функций	Производные сложных функций

Основные правила дифференцирования

с - константа

Геометрический смысл производной.

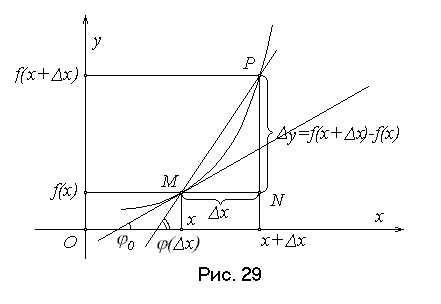
Касательной к графику функции в точке M будем называть предельное положение секущей MP при стремлении точки P к точке M по графику (или, что то же самое, при ).

.

.

Производная равна угловому коэффициенту касательной к графику функции в точке M.

Понятие дифференциала функции.

Главная линейная относительно часть приращения дифференцируемой функции называется дифференциалом функции в точке x, соответствующим приращению аргумента .

.

Дифференциал независимой переменной x равен = . Отсюда .

2. Задания для самостоятельной работы.

Задание 1. Вычислить пределы:

2.1.			2.2.
2.3.			2.4.
2.5.			2.6.
2.7.			2.8.
2.9.			2.10.
2.11.			2.12.
2.13.			2.14.
2.15.			2.16.
2.17.			2.18.
2.19.			2.20.

Задание 3. Исследовать функцию на непрерывность и построить график.

3.1.		3.2.
3.3.		3.4.
3.5.		3.6.
3.7.		3.8.
3.9.		3.10.
3.11.		3.12.
3.13.		3.14.
3.15.		3.16.
3.17.		3.18.
3.19.		3.20.

Задание 4. Найти производные функции. В случаях а) и г) найти производные второго порядка.

4.1.	a) в)	б) г)
4.2.	a) в)	б) г)
4.3.	a) в)	б) г)
4.4.	a) в)	б) г)
4.5.	a) в)	б) г)
4.6.	a) в)	б) г)
4.7.	a) в)	б) г)
4.8.	a) в)	б) г)
4.9.	a) в)	б) г)
4.10.	a) в)	б) г)
4.11.	a) в)	б) г)
4.12.	a) в)	б) г)
4.13.	a) в)	б) г)
4.14.	a) в)	б) г)
4.15.	a) в)	б) г)
4.16.	a) в)	б) г)
4.17.	a) в)	б) г)
4.18.	a) в)	б) г)
4.19.	a) в)	б) г)
4.20.	a) в)	б) г)

Задание 5. Составить уравнение касательной и нормали к кривой в точке, соответствующей параметру t=t₀.

5.1.		5.2.
5.3.		5.4.
5.5.		5.6.
5.7.		5.8.
5.9.		5.10.
5.11.		5.12.
5.13.		5.14.
5.15.		5.16.
5.17.		5.18.
5.19.		5.20.

Задание 6. Решить задачу:

1. Объем продукции цеха в течение рабочего дня представляет функцию где t – время. Найти производительность труда через 2 часа после начала работы и за 2 часа до окончания работы.

2. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией . Определить средние и предельные издержки при объеме продукции 10 единиц.

3. Зависимость между себестоимостью единицы продукции у и выпуском продукции х выражается функцией . Найти эластичность себестоимости при выпуске продукции, равном 60.

6.4. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью . Найти оптимальный для производителя объем выпускаемой продукции.

5. Объем продукции цеха в течение рабочего дня представляет функцию где t – время. Найти производительность труда за 2 часа до окончания работы, если рабочий день длится 8 часов.

6. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией . Определить средние и предельные издержки при объеме продукции 10 единиц.

7. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией . Определить средние и предельные издержки при объеме продукции 5 единиц.

8. Тело, выпущенное вертикально вверх, движется по закону . Определить скорость тела в момент соприкосновения с землей.

9. По оси ОХ движутся две материальные точки, законы которых . С какой скоростью эти точки удаляются друг от друга с момента встречи?

10. Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией . Определить средние и предельные издержки при объеме продукции 8 единиц.

11. Зависимость между себестоимостью единицы продукции у и выпуском продукции х выражается функцией . Найти эластичность себестоимости при выпуске продукции, равном 50.

12. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью . Найти оптимальный для производителя объем выпускаемой продукции.

6.14. Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением .Определить скорость реакции, когда t = 10 сек.

6.15. Объем продукции цеха в течение рабочего дня представляет функцию где t – время. Найти производительность труда через час после начала работы и за час до окончания работы.

6.16. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью . Найти оптимальный для производителя объем выпускаемой продукции.

6.17. Объем продукции цеха в течение рабочего дня представляет функцию где t – время. Найти производительность труда через 3 часа после начала работы и за час до окончания работы.

6.18 Зависимость между издержками производства у и объемом выпускаемой продукции х выражается функцией . Определить средние и предельные издержки при объеме продукции 8 единиц.

6.19 Зависимость между массой х кг вещества, получаемого в некоторой химической реакции и временем t выражается уравнением .Определить скорость реакции, когда t = 13 сек.

6.20. Производитель реализует свою продукцию по цене р за единицу, а издержки при этом задаются зависимостью . Найти оптимальный для производителя объем выпускаемой продукции.

Задание 7. Провести исследование и построить график функции.

7.1.		7.2.
7.3.		7.4.
7.5.		7.6.
7.7.		7.8.
7.9.		7.10.
7.11.		7.12.
7.13.		7.14.
7.15.		7.16.
7.17.		7.18.
7.19.		7.20.

Зачетное задание №3 Дифференцирование и интегрирование функции нескольких переменных