5.5. Построение проекций точек, лежащих на поверхностях вращения
Алгоритм построения недостающих проекций точек, принадлежащих поверхностям вращения, одинаков для различных видов поверхностей вращения.
5.5.1. Ось вращения I перпендикулярна горизонтальной п1 или фронтальной п2 плоскостям проекций
Пусть поверхность вращения задана так, что ось вращения i перпендикулярна какой-либо плоскости проекций, например i П1. В этом случае на П2 все параллели проецируются в виде прямых линий, перпендикулярных оси вращения, а на П1 они проецируются в виде окружностей.
а). Пусть на поверхности вращения задана точка А, причем задана ее фронтальная проекция А2 (рис. 5.45). Пусть на этой проекции точка А является видимой. Требуется построить ее горизонтальную проекцию.
Через проекцию А2 точки проводим проекцию m2 параллели поверхности перпендикулярно оси i2 до пересечения с главным меридианом поверхности в точках 12 и 12. Замеряем радиус параллели – это расстояние от оси вращения (точка О2) до главного меридиана 12, т.е. R=О212. Этим радиусом на П1 из центра i1О1 строим окружность - горизонтальную проекцию m1 параллели, на которой и находится проекция А1 точки А.
А2
11
i2
m2
i1О1
m1
А1
О2
12
12
i2
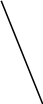
i1
(В2)
12
m2
Рис. 5.45
В1
11
m1
Рис. 5.45
Рис. 5.46
Поскольку на фронтальной проекции точка А является видимой, то горизонтальная проекция А1 этой точки будет располагаться на нижней части окружности параллели m1.
б). Если на чертеже поверхности вращения задана горизонтальная проекция В1 точки В (рис. 5.46), то В2 строится в обратном порядке.
Из i1, как из центра радиусом R=i1B1 строим проекцию m1 параллели. Находим точку 11 пересечения m1 с горизонтальной проекцией главного меридиана. Проекцию 12 точки 1 строим на фронтальной проекции главного меридиана. Через 12 перпендикулярно i2 проводим фронтальную проекцию m2 параллели, на которой по линии связи строим проекцию В2 точки В.
Так как проекция В1 точка В на П1 расположена на верхней части окружности параллели m1, то в этом случае на фронтальной проекции точка В лежит на невидимой части поверхности вращения, поэтому проекция В2 обозначена в скобках.
Если ось i поверхности вращения перпендикулярна фронтальной плоскости проекций, то алгоритм построения недостающей проекции точки, лежащей на поверхности, аналогичен описанному выше, только все построения необходимо начинать на той плоскости проекций, где задана проекция точки в той же последовательности.
5.5.2. Ось вращения I параллельна фронтальной п2 или горизонтальной п1 плоскостям проекций
Пусть заданы проекции конуса вращения, у которого ось вращения параллельна горизонтальной плоскости проекции (рис. 5.47). Пусть на поверхности задана точка А, причем задана ее фронтальная проекция (А2), лежащая на невидимой стороне проекции конуса. Требуется построить горизонтальную проекцию А1 этой точки.
d2
11
(А2)
12
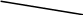
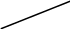
d1
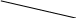
А1
Рис. 5.47
Построение недостающей проекции точки в таких случаях выполняется с помощью вспомогательных образующих.
Из вершины конуса вращения через А2 проводим вспомогательную образующую d2 до пересечения с основанием конуса. Так как не П2 проекция точки невидимая, то вспомогательная образующая пересекает дальнюю дугу основания конуса в точке 12. По линии связи на горизонтальной проекции основания конуса строим точку 11. Через эту точку проводим горизонтальную проекцию d1 вспомогательной образующей, на которой и строим проекцию А1 точки А. Эта проекция будет видимая, т.к. находится на верхней половине конуса.
Если точка задана на горизонтальной проекции, то все построения выполняются точно также, начиная с проведения вспомогательной образующей на горизонтальной проекции.