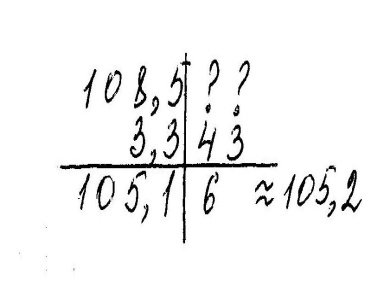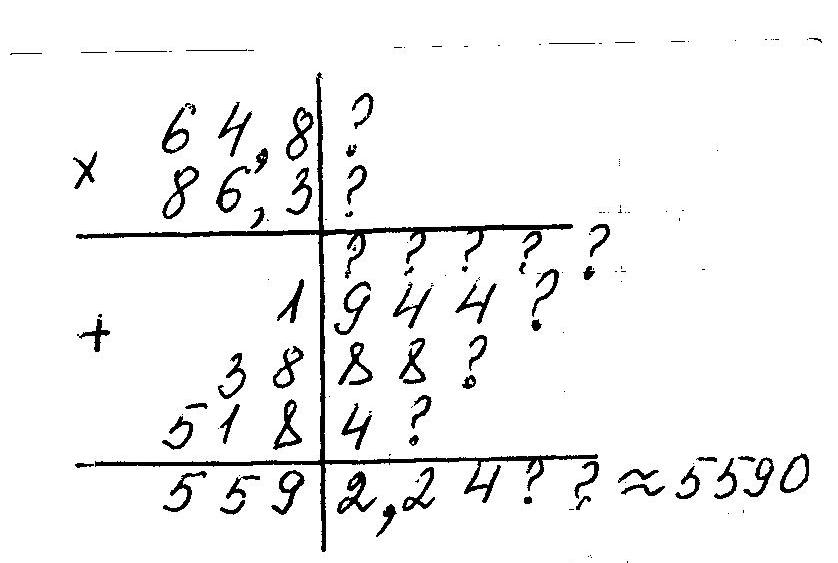Приближенные вычисления
§ 1. Введение.
§ 2. Значащие цифры в записи приближенного числа
§ 3. Округление чисел.
§ 4. Приближения чисел
§ 5. Абсолютная погрешность
§ 6. Относительная погрешность
§ 7.Особенности записи приближенных чисел. Число верных знаков после запятой.
§8.Сложение и вычитание приближенных чисел
§ 9. Произведение и частное приближенных чисел.
Задания.
Литература.
С.М.Никольский, М.К.Потапов и др. Алгебра 9. §9 стр. 204-224. Приближенные вычисления.
С.М.Никольский, М.К.Потапов и др. Алгебра 7. §3.п.3.5 Приближения чисел.
Я.Ф Чекмарев. Б.А. Тулинов. Арифметика для педагогических училищ.
В.А.Игнатьев. Сборник задач по арифметике для педагогических училищ.
§1. Введение. Зачем нужно уметь выполнять приближенные вычисления? Числа, с которыми мы имеем дело в жизни, бывают двух типов. Одни в точности дают истинную величину, другие — только приблизительно. Первые называют точными, вторые -приближенными. Часто мы сознательно берем приближенное число вместо точного, так как последнее нам не требуется. Во многих же случаях точное число невозможно найти по сути вопроса. Пример 1. В этой книге 512 страниц; число 512 — точное. Пример 2. В шестиугольнике 9 диагоналей; число 9 — точное. Пример 3. Продавец взвесил на автоматических весах 50 г масла. Число 50 — приближенное, так как весы нечувствительны к увеличению или уменьшению веса на 0,5 г. Пример 4. Расстояние от станции Москва до станции Санкт-Петербург Октябрьской ж. д. составляет 651 км. Число 651 — приближенное, так как, с одной стороны, наши измерительные инструменты неточны, с другой же стороны, сами станции имеют некоторое протяжение. Все без исключения измерения приводят к приближенным значениям измеряемых величин. Полная точность при измерениях не достигается никогда. Результат действий с приближенными числами есть тоже приближенное число. Как охарактеризовать качество измерения, степень его точности? Как производить арифметические действия с числами, полученными приближенно? Не будет ли увеличиваться ошибка, если мы над приближенной величиной будем совершать арифметические действия? Нельзя ли, пользуясь тем, что сами данные приблизительны и ответ нас интересует приближенный, упростить арифметические действия? |
Теория приближенных вычислений позволяет: 1) зная степень точности данных, оценить степень точности результатов еще до выполнения действий; 2) брать данные с надлежащей степенью точности, достаточной, чтобы обеспечить требуемую точность результата, но не слишком большой, чтобы избавить вычислителя от бесполезных расчетов; 3) рационализировать сам процесс вычисления, освободив его от тех выкладок, которые не окажут влияния на точные цифры результата. |
§ 2. Значащие цифры в записи приближенного числа Значащей цифрой десятичной дроби называют первую (слева направо) отличную от нуля цифру, а также все следующие за ней цифры. Пример 1. В числе 235 000 все цифры значащие; в числе 0,302 цифры, стоящие после запятой, значащие; в числе 0,003004 цифры, начиная с цифры 3 значащие. Например, в числе 0,00385 три значащие цифры; в числе 0,03085 четыре значащие цифры; в числе 2500 — четыре; Число значащих цифр некоторого числа называется его значностью. |
Задание 1. Определите количество значащих цифр в записи чисел: 602; 0,0208; 4,040; 0,00020; 3000; 82,0; 0,7; 303;0330.
|
§ 3. Округление чисел Правило 1. Если первая из отбрасываемых цифр больше чем 5, то последняя из сохраняемых цифр усиливается, т. е. увеличивается на единицу. Усиление совершается и тогда, когда первая из отбрасываемых цифр равна 5, а за ней есть одна или несколько значащих цифр. (О случае, когда за отбрасываемой пятеркой нет цифр, см. ниже, правило 3.) Пример 1. Округляя число 27,874 до трех значащих цифр, пишем 27,9. Третья цифра 8 усилена до 9, так как первая отбрасываемая цифра 7 больше чем 5. Число 27,9 ближе к данному, чем неусиленное округленное число 27,8. Пример 2. Округляя число 36,251 до первого десятичного знака, пишем 36,3. Цифра десятых 2 усилена до 3, так как первая отбрасываемая цифра равна 5, а за ней есть значащая цифра 1. Число 36,3 ближе к данному (хотя и незначительно), чем неусиленное число 36,2.
|
Правило 2. Если первая из отбрасываемых цифр меньше чем 5, то усиления не делается. Пример 3. Округляя число 27,48 до единиц, пишем 27. Это число ближе к данному, чем 28. |
Правило 3. Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее четное число, т. е. последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная. Почему применяется это правило, сказано ниже (см. замечание) Правило 3 можно изменить и применять всегда округление на ближайшее нечетное число. Точность будет та же, но четные числа удобнее, чем нечетные Пример 4. Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиления не делаем, так как последняя сохраняемая цифра 6 — четная. Число 0,046 столь же близко к данному, как 0,047. Пример 5. Округляя число 0,935 до второго десятичного знака, пишем 0,94. Последняя сохраняемая цифра 3 усиливается, так как она нечетная.
|
Задание .Составить алгоритм действия округления числа
|
Задание 1. Округлить числа до первого десятичного знака. 6,527 0,456 2,195 1,450 0,950 4,851 0,850 0,05 |
Задание 2. Округлите число 0,06983 до трех значащих цифр, до двух, до одной.
|
4. Приближения чисел. Если число а удовлетворяет неравенствам а1аа2, то а1 называют приближением с недостатком или приближением снизу, а2 называют приближением с избытком или приближением сверху. Пример 1. Пусть а=2,3(28). Оборвем эту дробь на цифре второго разряда после запятой. Получим число 2,33, большее, чем а. Т.о. 2,32 а 2,33. Число 2,32 есть приближение числа а с недостатком, а 2,33 есть приближение числа а с избытком. 2,32 есть приближение числа а с точностью до одной сотой с недостатком (снизу). 2,33 есть приближение числа а с точностью до одной сотой с избытком (сверху). Вместо слов «с точностью до одной сотой» говорят еще «с точность до единицы второго разряда». Пример 2. Подобным образом для числа в = -2,3(38) имеем: -2,33 в -2,32. -2,33 есть приближение числа в с точностью до одной сотой с недостатком, -2,32 есть приближение числа в с точностью до одной сотой с избытком. |
Задание 1. Найдите приближения числа а=2,3(28) сверху и снизу с точностью до единицы четвертого разряда.
|
Задание 2. Найдите приближения числа в=-2,3(28) сверху и снизу с точностью до единицы третьего разряда.
|
§5. Абсолютная погрешность Абсолютной погрешностью или погрешностью приближенного числа называется модуль разности точного и приближенного значений. Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет |1300 – 1284| = 16. При округлении до 1280 абсолютная погрешность составляет 1284 - 1280 = 4. |
Найти абсолютную погрешность не всегда возможно. Например, при измерении длины отрезка получен результат 4,3см. Мы не можем найти абсолютную погрешность приближенного значения, так как не знаем точного длины отрезка. В таких случаях важно указать такое число, больше которого абсолютная погрешность быть не может. В рассматриваемом примере в качестве такого числа можно взять число 0.1. В самом деле цена деления линейки 0,1см и поэтому абсолютная погрешность приближенного значения, равного 4,3 не больше, чем 0,1. В таких случаях говорят, что число 4,3 есть приближенное значение длины отрезка (в сантиметрах) с точностью до 0,1. Вообще, если х а и абсолютная погрешность этого приближенного значения не превосходит некоторого числа h, то число а называют приближенным значением х с точностью до h. Пишут: х а с точностью до h.
|
Задание 1. Округлите число 46,427 до десятых и найдите абсолютную погрешность.
Задание 2. Представьте число 7\9 в виде десятичной дроби и округлите эту дробь до десятых, сотых и тысячных. В каждом случае найдите абсолютную погрешность.
|
§ 6. Относительная погрешность Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к модулю приближенного значения. Иногда относительную погрешность выражают в процентах, для этого полученное значение нужно умножить 100%.
Пример
1. В школе 197 учащихся.
Округляем это число до 200.
Абсолютная погрешность
составляет 200 - 197 = 3. Относительная
погрешность равна
|
Задание 1. Округлите число 46,427 до десятых и найдите относительную погрешность
|
Задание
2.
Представьте число
|
§ 7. Особенности записи приближенных чисел. Число верных знаков после запятой. Приближенные числа обычно записываются в форме десятичных дробей. При этом последняя цифра характеризует величину абсолютной погрешности. Если в приближенных вычислениях мы имеем дело с числом 12,45, то это не значит, что величина характеризуемая этим числом, не содержит тысячных долей. Можно только утверждать, что тысячные доли при измерении не учитывались; следовательно абсолютная погрешность меньше одной сотой. Точно также относительно приближенного числа 1, 283 мы скажем, что абсолютная погрешность меньше одной тысячной. Приближенные числа принято записывать так, чтобы абсолютная погрешность не превышала единицы последнего десятичного разряда. Эту мысль выражают иногда иначе, говоря: абсолютная погрешность приближенного числа характеризуется числом десятичных знаков после запятой (один знак после запятой -абсолютная погрешность на превосходит одной десятой; два знака - одной сотой и т.д.) |
Как же быть, если при тщательном измерении величины получится, что она содержит целую единицу, две десятых, пять сотых, не содержит тысячные, а десятитысячные не поддаются учету? Записать так 1,25 нельзя – это будет обозначать, что тысячные не учтены, тогда как на самом деле мы уверены, что их нет. В этом случае принято ставить на месте тысячных нуль:1,250. Таким образом в теории приближенных вычислений числа 1,25 и 1,250 означают далеко не одно и то же. Первое число содержит тысячные, но мы не знаем сколько именно. Во втором числе мы знаем, что тысячных ноль, сомнение вызывают десятитысячные. О числе 1,25 можно разными способами выразить одну и ту же мысль: -число 1,25 дано с точностью до сотых; - число 1,25 дано с двумя знаками после запятой; - число 1,25 дано с абсолютной погрешностью, меньшей 0,01. |
Некоторые трудности возникают при записи целых приближенных чисел. Пусть число жителей села – равно 2 000 человек, а в большом городе – приблизительно 457 000 жителей. Причем относительно города мы ручаемся за тысячи, но ошибаемся в счете сотен, а тем более десятков и единиц. Как в самой записи отразить разницу между точным числом (2000) и приближенным (457 000)? Ведь нули в конце первого числа и в конце второго числа имеют разное значение: в первом случае мы знаем точно, что количество сотен, десятков и единиц равно нулю; во втором - на наше незнание числа сотен , десятков и единиц. Из
этого затруднения выходят по разному.
Иногда неизвестные цифры приближенного
числа заменяют маленькими нуликами
(пишут 457 000
вместо 457 000); иногда пишут только
верные цифры, а нули заменяют множителем,
имеющим вид степени десяти (пишут
457 |
Задание 1. Объясните, в чем разница между приближенными числами 2,7 и 2,70.
Задание
2. Что
можно сказать о числах: 28 300 , 283 |
В приближенных числах различают цифры верные (точные), не вполне верные (сомнительные) и безусловно неверные. Пример 1. Несколько учетчиков считают число присутствующих на массовке. Один насчитал 3 275 человек, второй – 3 264 человека, третий – 3 272 человека, четвертый – 3 281 человек, пятый – 3 277. Сколько человек наверняка участвовало в массовке. Каждый учетчик насчитал 3 тысячи. Поэтому цифра 3 – верная. Точно также и цифра сотен 2, которую получили все учетчики, безусловно, верная. Цифра же десятков получилась не одинаковая: у трех учетчиков по 7, а у одного 6, у другого 8. Поэтому цифра десятков не вполне верная, сомнительная, а цифра единиц безусловно неверная, т.к. у всех учетчиков она разная. Отвечая на вопрос можно утверждать, что в массовке участвовали 3 270 человек, но ручаться можно только за первые две цифры: за тысячи и сотни. Все цифры приближенного числа, в которых мы уверены, будем называть верными цифрами, независимо от их положения.
|
Существует связь между числом верных цифр и его относительной погрешностью. Например,
каждое из следующих пяти чисел имеет
три верные цифры: 283 Существует следующее правило: если число верных цифр больше или равно трем, то процентная погрешность меньше единицы, деленной на единицу со столькими нулями, сколько в числе верных цифр без трех. Если же в числе две верные цифры, то относительная погрешность меньше 10% Если дана одна верная цифра, то погрешность может достигать несколько десятков процентов; этот случай для практики не представляет интереса. Пример
1. Относительная
погрешность числа 0,0028365,
не
превосходит Пример
2.
Относительная погрешность числа 2
800
не
превосходит Пример 3. Относительная погрешность числа 2,8 не превосходит 10 % (две верные цифры). Особенно важен случай, когда допустима погрешность до 1%; большинство технических расчетов проводится именно с этой степенью точности. В этом случае приближенные числа должны иметь три верные цифры. |
Задание. Оценить погрешность следующих приближенных чисел: 0,818; 2,410; 56 ; 32,200; 0,00012; 843,356.
|
§ 8. Сложение и вычитание приближенных чисел с заданной точностью Правило 1. Чтобы вычислить приближенно сумму (разность) двух чисел с заданной точностью надо: -округлить первое число с заданной точностью, - округлить второе число с заданной точностью, -сложить (вычесть) полученные приближения. Пример 1. Найти приближенно сумму и разность чисел 23,508 и 0,76 с точностью до целых. Решение: 23,52824, 0,761. 24+1=25. |
Задание 1. Найти приближенно сумму и разность чисел а=23,1834567 и в=4,2375 с точностью до сотых. Решение:
|
Правило 2. Сложение и вычитание по правилу подсчета цифр. При сложении и вычитании приближённых чисел в результате следует сохранять столько десятичных знаков, сколько их в приближённом данном с наименьшим числом десятичных знаков.
|
Задание. Составить алгоритм действия сложения и вычитания по правилу подсчета цифр
|
1 случай. Компоненты даны с одинаковой точностью.
|
Цифра сотых долей в каждом слагаемом сомнительна. Она остается сомнительной и в сумме. |
|
В остатке сомнительная цифра того же разряда, как и в компонентах. |
2 случай. Точность компонентов различна.
7
|
В сумме нет смысла оставлять сотые и тысячные доли, так как во втором слагаемом сотые и тысячные неизвестны. |
108,5-3,3=105,2
|
Во избежание накопления ошибок при округлении чисел в числах имеющих больше десятичных знаков, оставляют один знак запасным. |
Задание 2. Найти приближенные значения х+у и х-у, если: х34,12 и у19,6.
|
§ 9. Произведение и частное приближенных чисел. Правило 1. Чтобы вычислить приближенно произведение (частное) двух чисел с заданной точностью, надо: - округлить первое число с точностью до заданной значащей цифры, - округлить второе число с точностью до заданной значащей цифры, -перемножить (разделить) полученные приближения, -результат округлить до той же значащей цифры. Пример 1. Пусть х 0,8673 и у 7,1. найдем приближенное значение произведения ху с точностью до третьей значащей цифры. 0,8673 0,867 7,1 7,10 0,8677,10 = 6,15570 6,16 ху 6,16 |
Пример 2. Пусть х 0,8673 и у 7,1. найдем приближенное значение х:у и у:х с точностью до третьей значащей цифры. 0,8673 0,867 7,1 7,10 0,867: 7,10 0, 1221126.. 0, 122; х:у 0, 122. 7,10:0,867 8, 189158.. 8,19. у:х 8,19.
|
Задание 1. Пусть а 2,75 и в 0,12.
Найти
приближенно: а∙в, ав,
ва Решение:
|
Правило 2. Произведение и частное приближенных чисел по правилу подсчета цифр. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их имеет приближённое данное с наименьшим числом значащих циф Задание. Составить алгоритм действия умножения и деления по правилу подсчета цифр
|
Примеры |
|
Найти площадь прямоугольника, длина которого 64,8см, ширина 86,3см.
|
Рассматривая, как получились цифры произведения, мы видим, что цифры тысяч, сотен и десятков надежные, цифра единиц не вполне надежная. Это зависит от величины отброшенных сотен долей. Десятые и сотые доли произведения нет смысла удерживать в окончательном ответе. |
Вычислить
произведение 1 1 1\71,143; 5\6 0, 83.
|
В произведении нет смысла брать больше двух значащих цифр. |
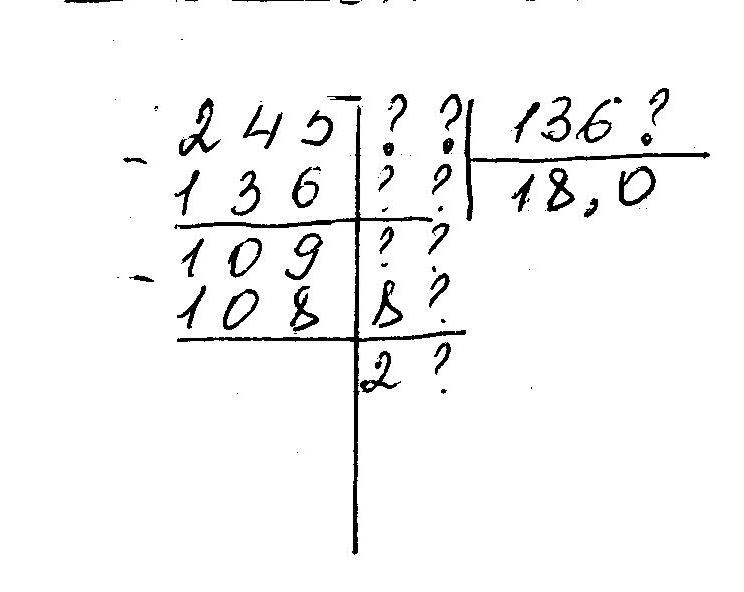
2,45:0,136
|
Согласно правилу частное должно иметь три значащие цифры. |
4
:
3
|
Согласно правилу в частном должны получить три верные цифры. |
Задание 2. Пусть а 2,75 и в 0,12.. Найти приближенно: а∙в, ав, ва. Решение:
|

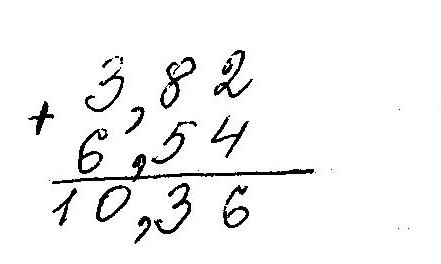
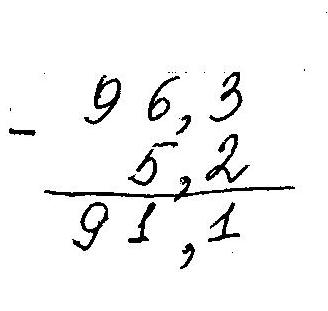

 ,54+12,3+0,724=20,6
,54+12,3+0,724=20,6