3.2.3 Побудова функціональної схеми автомата

На основі отриманих функцій збудження і функцій виходів можна побудувати функціональну схему мікропрограмного автомата. На практиці найчастіше використовують базиси Буля (елементи І, АБО, НІ), Шеффера (елементи І-НІ) і Пірса (елементи АБО-НІ). Якість вирішення задачі синтезу комбінаційної схеми оцінюють за витратами обладнання та швидкодією.

При розробці схем на основі конкретної елементної бази кількість устаткування зазвичай вимірюється числом корпусів (модулів), що використовуються у схемі. У теоретичних розробках орієнтуються на довільну елементну базу і тому для оцінки затрат обладнання використовується оцінка складності схем за Квайном. Складність (ціна) схеми за Квайном визначається сумарним числом входів логічних елементів у складі схеми. При такій оцінці одиниця складності, тобто одиниця обладнання - один вхід логічного елемента. При цьому ціна інверсного входу зазвичай приймається рівній двом.

Такий підхід до оцінки складності схем є результативним з наступних причин. По-перше, складність схеми легко обчислюється за булевими функціями, на основі яких будується схема: складність схеми дорівнює сумі кількості літер у диз’юнктивній нормальній формі, при цьому літері зі знаком заперечення відповідає ціна два, і кількості знаків диз’юнкції, збільшеного на одиницю для кожного диз’юнктивного виразу. По-друге, всі класичні методи мінімізації булевих функцій забезпечують мінімальність схеми саме в сенсі ціни схеми за Квайном.

Схема, мінімальна в сенсі ціни за Квайном, зазвичай реалізується найменшим числом конструктивних елементів - корпусів.

Швидкодія схеми оцінюється максимальною затримкою сигналу при проходженні його від входу схеми до виходу, тобто визначається проміжком часу від моменту надходження вхідних сигналів до моменту встановлення відповідних значень вихідних сигналів. Затримка сигналу кратна числу елементів, через які проходить сигнал від входу до виходу схеми. Тому швидкодія схеми характеризується значенням d, де  - затримка сигналу на одному логічному елементі. Значення d визначається кількістю рівнів комбінаційної схеми, яка розраховується наступним чином. Входам комбінаційної схеми присвоюється рівень 0. Елементи, зв’язані тільки з входами схеми, відносяться до рівня 1. Елемент відноситься до рівня d, якщо він пов’язаний входами з елементами рівнів d-1, d-2, ..., 0. Максимальний рівень елементів визначає кількість рівнів комбінаційної схеми.

4 Приклад синтезу автомата за заданим алгоритмом

За заданою змістовною схемою алгоритму в мікроопераціях (рис. 4.1), необхідно розробити функціональну схему автомата Мілі (Мура) в якості елементів пам’яті використовувати D-тригери, комбінаційну схему реалізувати на логічних елементах. Дати оцінку конструктивної складності ЦА

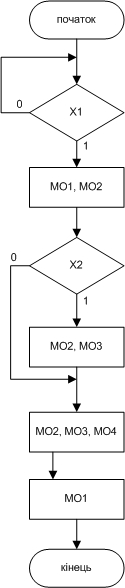
Рисунок 4.1 - Схема алгоритму в мікроопераціях

Замінимо набори мікрооперацій О1, О2, О3, О4 на коди мікрокоманд Y1, Y2, Y3, Y4. В результаті отримаємо кодовану ГСА в мікрокомандах.

Побудуємо зазначену граф-схему алгоритму (ГСА) автомата Мілі (Мура).

Відповідно до вимог що пред’являються до розмітки станів цифрового автомата Мілі (Мура) отримуємо позначену ГСА цифрового автомата (рис. 4.2).

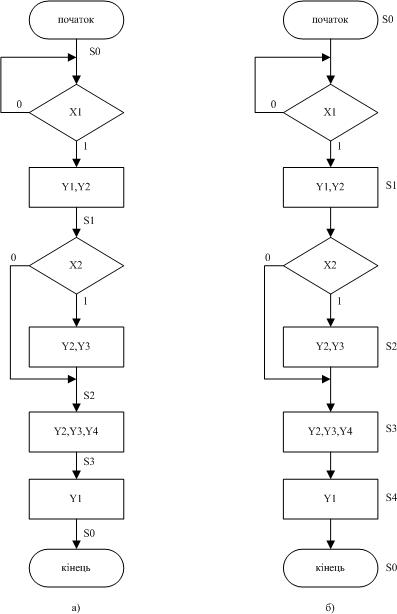
Рисунок 4.2 - Позначені граф-схеми а) для автомата Мілі, б) для автомата Мура

Побудова графа функціонування автомата

Згідно позначеної граф-схеми алгоритму автомата Мілі (Мура) будуємо граф функціонування автомата (рис. 4.3).

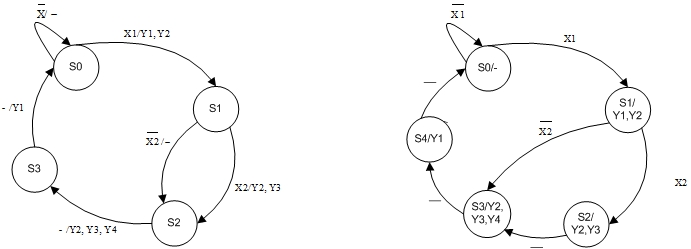
Рисунок 4.3 - Графи функціонування автоматів: а) Мілі; б) Мура

Проводимо кодування станів пристрою.

Число розрядів коду стану відповідає числу елементів пам’яті і визначається за формулою: k = ┐ log₂S ┌, де k - число розрядів (число елементів пам'яті) S - число внутрішніх станів; ┐┌ - округлення у більшу сторону. У нашому випадку для автомата Мілі число станів S=4 Кількість розрядів коду стану (число елементів пам’яті):

k = ┐ log₂S ┌ = ┐ log₂4 ┌ = 2. Для автомата Мура число станів S = 5. Кількість розрядів коду стану (число елементів пам'яті):

k = ┐ log₂S ┌ = ┐ log₂5 ┌ = 3.

Таблиці кодування станів автомата Мілі і автомата Мура наведені в табл. 4.1, 4.2 відповідно.

На наступному етапі формуємо функції переходу, збудження і виходів пристрою. За позначеною ГСА або графом функціонування автомата, таблицею кодування станів автомата та таблицею переходів тригерів будуємо таблиці (або таблицю) функцій переходу, збудження і виходів пристрою.

Таблиця 4.1 - Таблиця кодування станів автомата Мілі

Стан	Код стану
S0	00
S1	01
S2	10
S3	11

Таблиця 4.2 - Таблиця кодування станів автомата Мура

Стан	Код стану
S0	000
S1	001
S2	010
S3	011
S4	100

Таблиця 4.3 - Таблиця функцій виходів, переходу і збудження для автомата Мілі

Початковий стан			Умови переходу	Наступний стан			Функції виходу		Функції збудження
Позначка	Код			Позначка	Код
	Q1	Q2			Q1	Q2			D1	D2
S0	0	0		S0	0	0		—		0	0
S0	0	0		S1	0	1		Y1,Y2		0	1
S1	0	1		S2	1	0		Y2,Y3		1	0
S1	0	1		S2	1	0		—		1	0
S2	1	0	—	S3	1	1		Y2,Y3,Y4		1	1
S3	1	1	—	S0	0	0		Y1		0	0

Таблиця 4.3 - Таблиця функцій виходів для автомата Мура

Стан	Код стану			Функції виходу
	Q3	Q2	Q1	Y1	Y2	Y3	Y4
S0	0	0	0	0	0	0	0
S1	0	0	1	1	1	0	0
S2	0	1	0	0	1	1	0
S3	0	1	1	0	1	1	1
S4	1	0	0	1	0	0	0

Таблиця 4.4 - Таблиця функцій переходу і збудження для автомата Мура

Початковий стан				Стан переходу		Наступний стан						Функції збудження
Позначка	код					Позначка		код
	Q1	Q2	Q3					Q1	Q2	Q3		D1	D2	D3
S0	0	0	0				S0		0	0	0		0	0	0
S0	0	0	0				S1		0	0	1		0	0	1
S1	0	0	1				S2		0	1	0		0	1	0
S1	0	0	1				S3		0	1	1		0	1	1
S2	0	1	0		­—		S3		0	1	1		0	1	1
S3	0	1	1		—		S4		1	0	0		1	0	0
S4	1	0	0		—		S0		0	0	0		0	0	0

Далі проводимо мінімізацію функцій збудження елементів пам’яті і функцій виходів.

З таблиці функцій переходу, збудження і виходів автомата Мілі (Мура) отримуємо систему логічних рівнянь для цифрового автомата Мілі (Мура).

Система логічних рівнянь для цифрового автомата Мілі:

Система логічних рівнянь для цифрового автомата Мура:

З системи логічних рівнянь для цифрового автомата Мілі отримуємо повне безліч кон’юнкцій для даного автомата:

З системи логічних рівнянь для цифрового автомата Мілі отримуємо повне безліч кон’юнкцій для даного автомата:

З повної множини кон’юнкцій отримуємо таблицю покриття кон’юнкціями системи логічних рівнянь.

Таблиця 4.5 - Таблиця покриття кон’юнкціями для цифрового автомата Мілі

	K1	K2	K3	K4	K5	K6
D1		+	+
D2	+	+
D3
Y1					+	+
Y2		+	+	+
Y3		+		+
Y4	+

Таблиця 4.5 - Таблиця покриття кон’юнкціями для цифрового автомата Мура

	K1	K2	K3	K4	K5	K6	K7	K8	K9
D1				+	+	+
D2		+	+
D3	+
Y1		+							+
У2							+	+
Y3							+
У4	+

На основі отриманих функцій збудження і функцій виходів будуємо функціональну схему автомата Мілі (Мура).

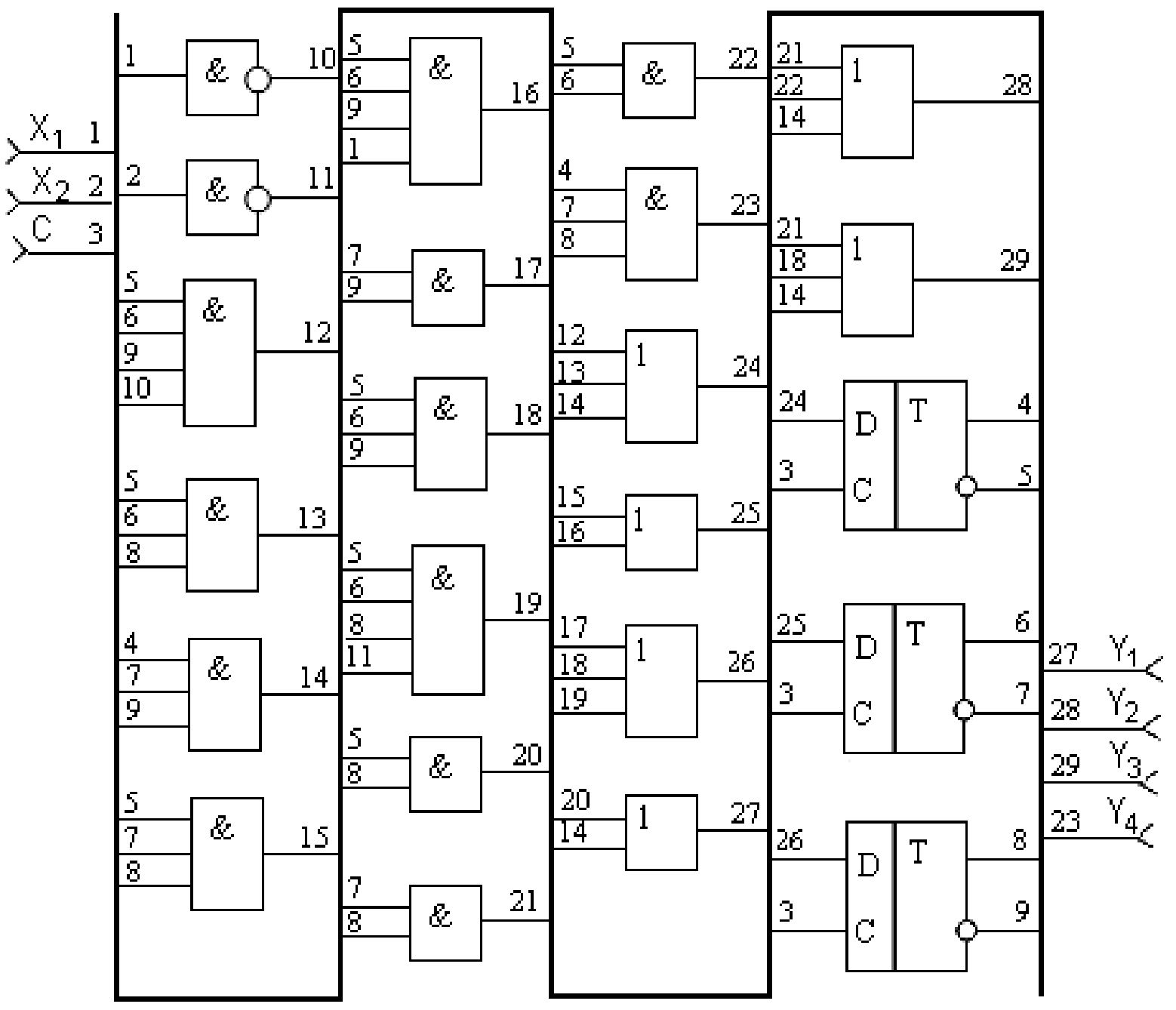
Рисунок 4.4 – Приклад функціональної схеми автомата Мілі (не відповідає розглянутому прикладу)

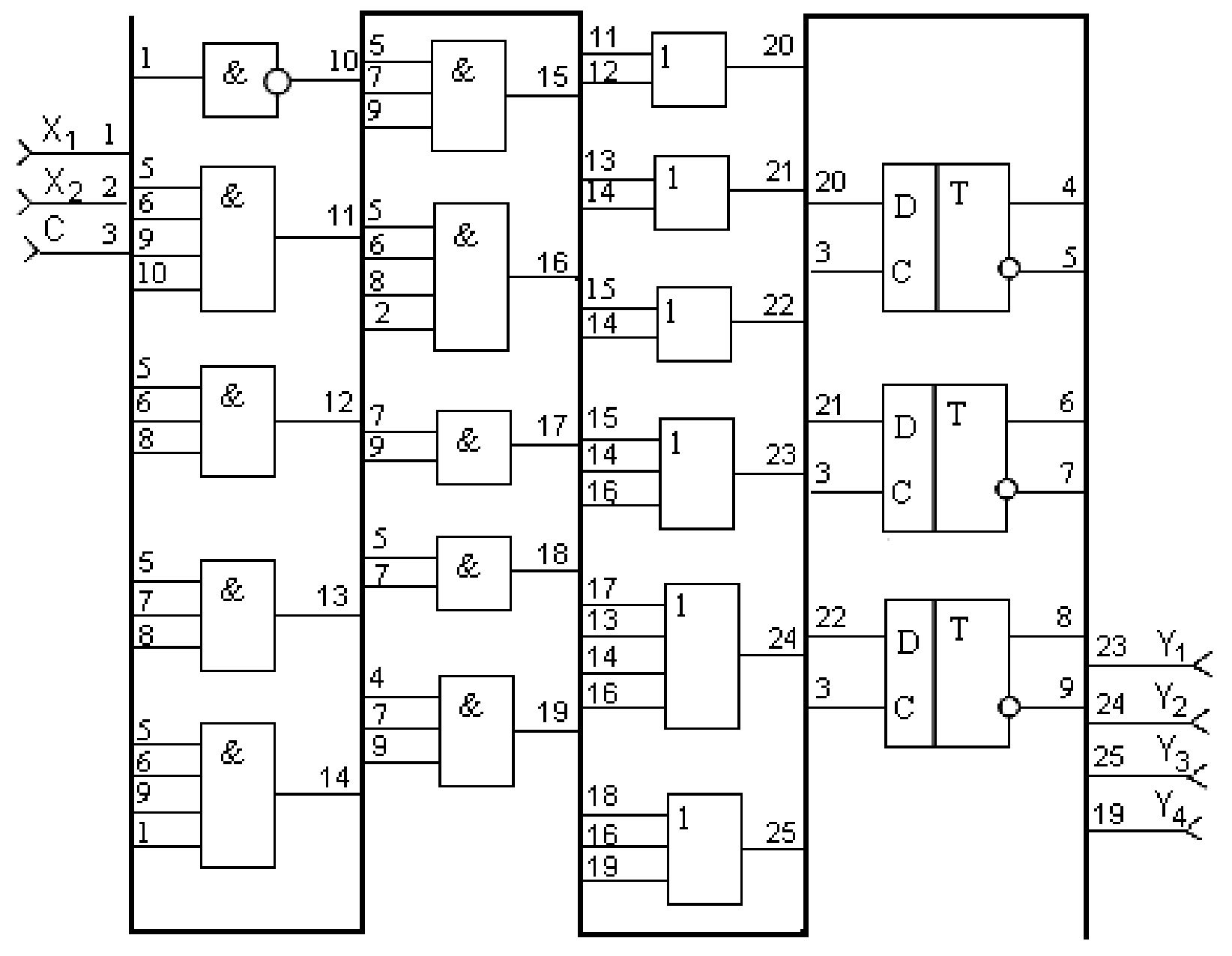
Рисунок 4.5 – Приклад функціональної схеми автомата Мура (не відповідає розглянутому прикладу)

Проводимо оцінку конструктивної складності автомата Мілі (Мура).

- визначення конструктивної складності автомата Мура методом Квайна - число входів логічних елементів: 59.

- число ярусів сигналу на самому довгому шляху від входу до виходу: 4.

- кількість елементів, необхідних для побудови функціональної схеми:

Таблиця 8 - Обладнання для реалізації автомата Мура

• визначення конструктивної складності автомата Мілі методом Квайна - число входів логічних елементів: 51.

• число ярусів сигналу на самому довгому шляху від входу до виходу: 4.

• кількість логічних елементів необхідних для побудови функціональної схеми:

Таблиця 9 — Обладнання для реалізації автомата Мілі