2.2.3. Геометрические объекты: пирамида, призма, цилиндр, конус и другие

Пирамида – это многогранник, одна грань которого – многоугольник, а остальные грани – треугольники с общей вершиной (рис. 53). Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина ее отсекается плоскостью.

Многогранником называется геометрический объект, ограниченный совокупностью плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого (но только одного).

Построение графического отображения многогранника сводится к построению проекций его вершин и ребер. Кратко охарактеризуем геометрические свойства некоторых многогранников и выполним их проекции.

Призма – многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники со взаимно параллельными сторонами, а все другие грани – параллелограммы (рис. 54). Название призмы зависит от того, какой многоугольник лежит в ее основании: если треугольник, то призма – треугольная, если четырехугольник, то – четырехугольная и т.д. Если основанием призмы является параллелограмм, то такая призма – параллелепипед. Призма называется прямой, если ее ребра перпендикулярны плоскости основания. Прямоугольный параллелепипед, все ребра которого конгруэнтны между собой, называется кубом.

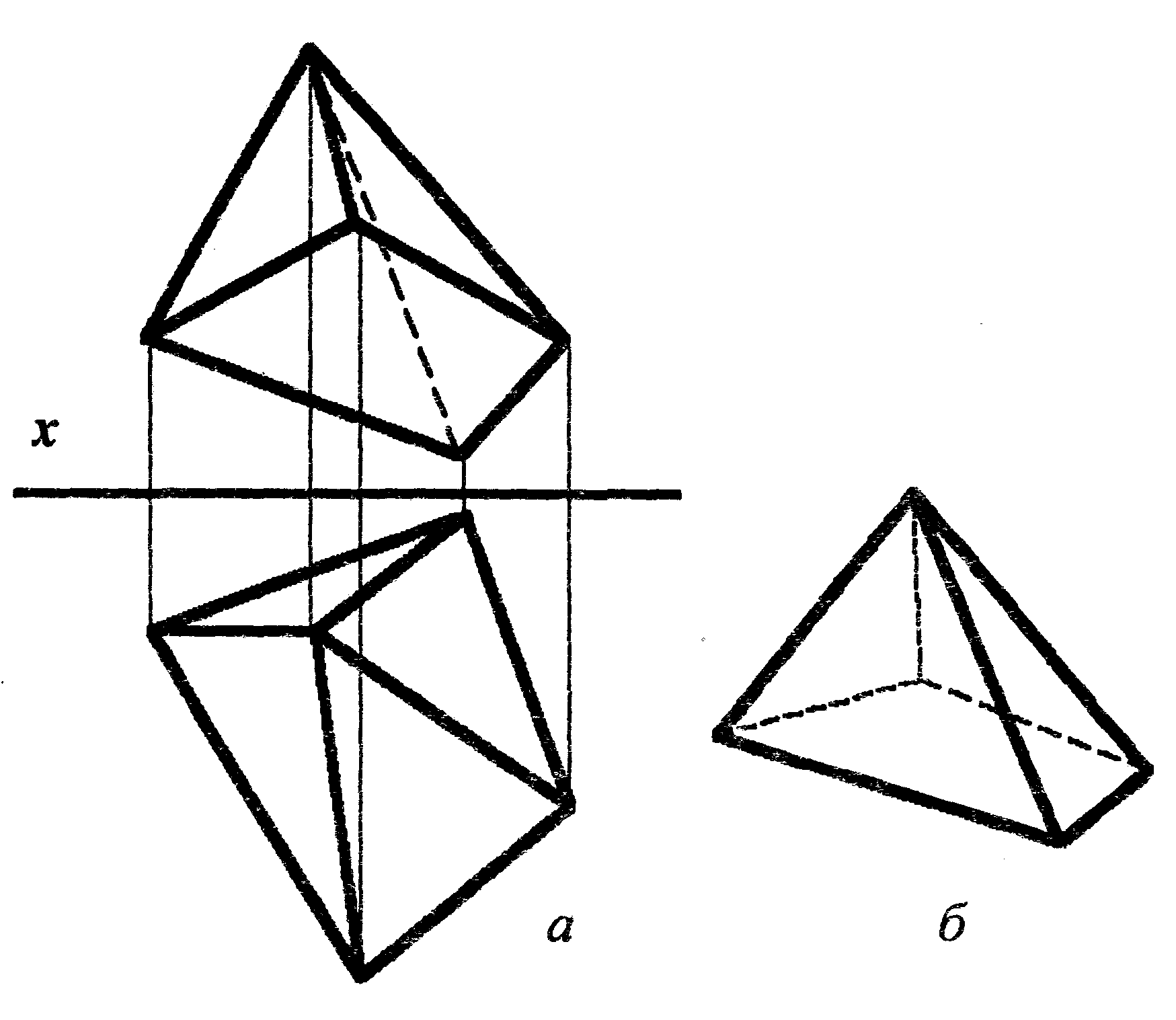
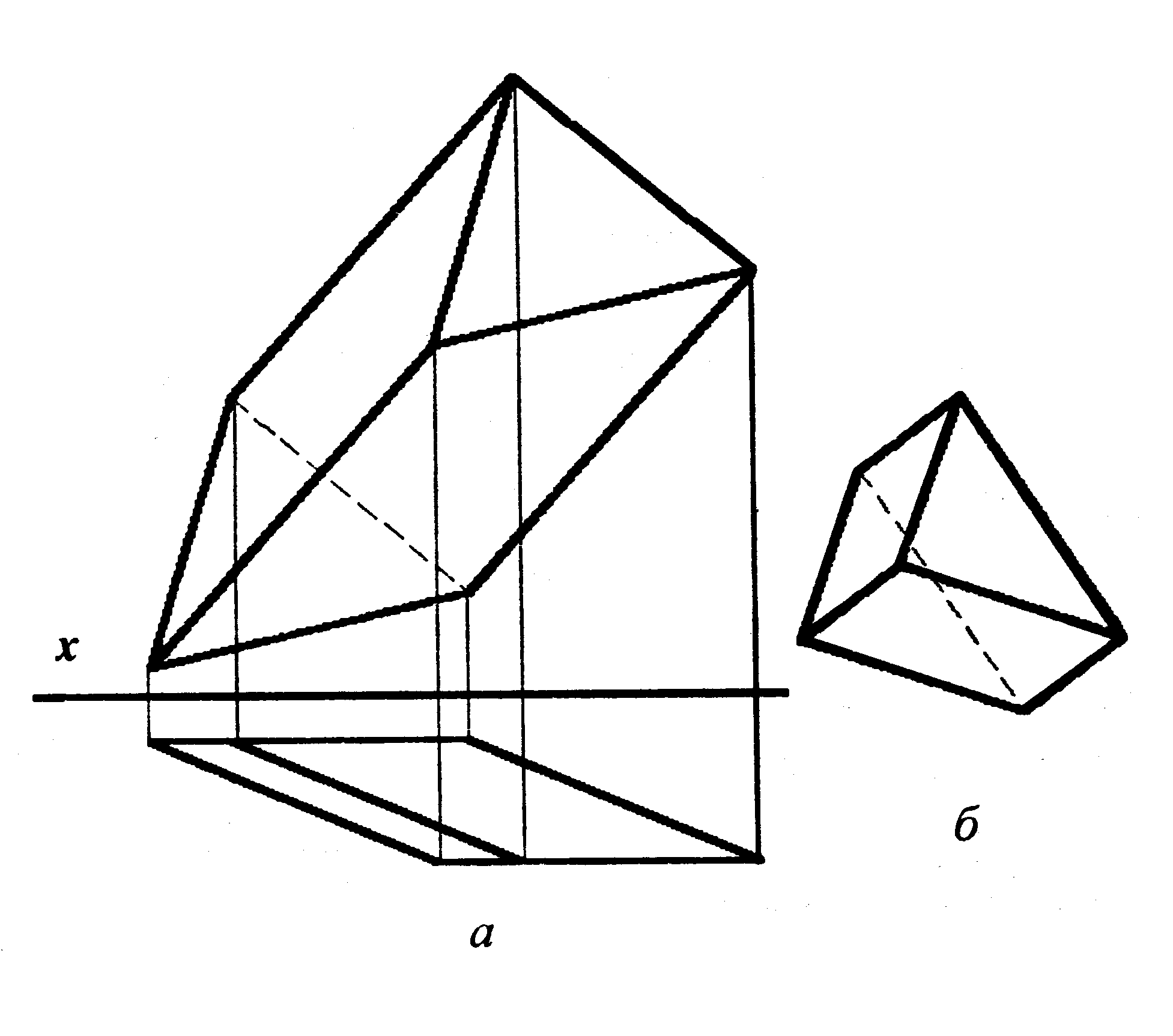
Рис. 54. Призма:

а) проекционный чертеж;

б) аксонометрия

Рис. 53. Пирамида:

а) проекционный чертеж;

б) аксонометрия

Призматоид – многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой треугольники и трапеции, вершины которых являются вершинами многоугольников, лежащих в основаниях (рис. 55).

М ногогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильным. Углы при вершинах такого многогранника равны между собой. Существует пять типов правильных многогранников, свойства которых описал более двух тысяч лет назад древнегреческий философ Платон, чем и объясняется их общее название. Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками. Это правильная треугольная пирамида.

Гексаэдр – правильный шестигранник. Это куб, ограниченный шестью равными квадратами.

Октаэдр – правильный восьмигранник, ограниченный восемью равносторонними и равными между собой треугольниками, соединенными по четыре у каждой вершины (рис. 56).

Икосаэдр – правильный двадцатигранник, ограниченный двадцатью равносторонними и равными треугольниками, соединенными по пять у каждой вершины (рис. 57).

Додекаэдр – правильный двенадцатигранник, ограниченный двенадцатью правильными и равными пятиугольниками, соединенными по три у каждой вершины (рис. 58).

К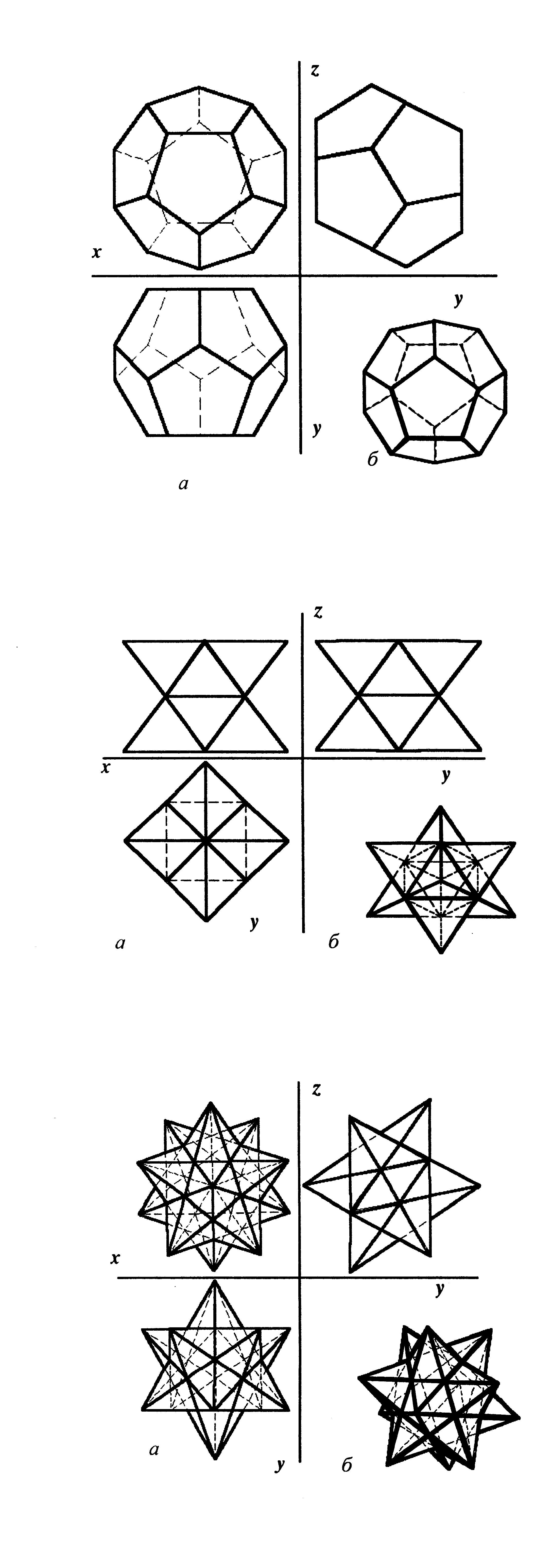 роме правильных выпуклых многогранников, существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Достраивая пересечения продолжений граней Платоновых тел, можно получать звездчатые многогранники. В качестве примера рассмотрим две наиболее простые звездчатые формы.

З

Рис. 58. Додекаэдр:

а) проекционный чертеж;

б) аксонометрия

вездчатый октаэдр. Восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые «куски», внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра (рис. 59). Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Такой звездчатый многоугольник в 1619 г. описал Кеплер и назвал его stella ostanguta – восьмиугольная звезда.

М

Рисунок 35

Рис. 59. Звездчатый октаэдр:

а) проекционный чертеж;

б) аксонометрия

алый звездчатый додекаэдр – звездчатый додекаэдр первого продолжения. Он образован продолжением граней правильного выпуклого додекаэдра до их пересечения. Каждая грань выпуклого додекаэдра при продолжении сторон образует правильный звездчатый пятиугольник (рис. 60). Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые «куски», внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра.

Ц

Рис. 60. Малый звездчатый

додекаэдр:

а) проекционный чертеж;

б) аксонометрия

илиндр – геометрический объект, ограниченный цилиндрической поверхностью и двумя плоскостями, называемыми основаниями. В зависимости от угла наклона образующих цилиндрической поверхности к основанию различают прямой цилиндр (угол наклона 90°) и наклонный (рис. 61).

К

Рис. 61. Наклонный цилиндр:

а) проекционный чертеж;

б) аксонометрия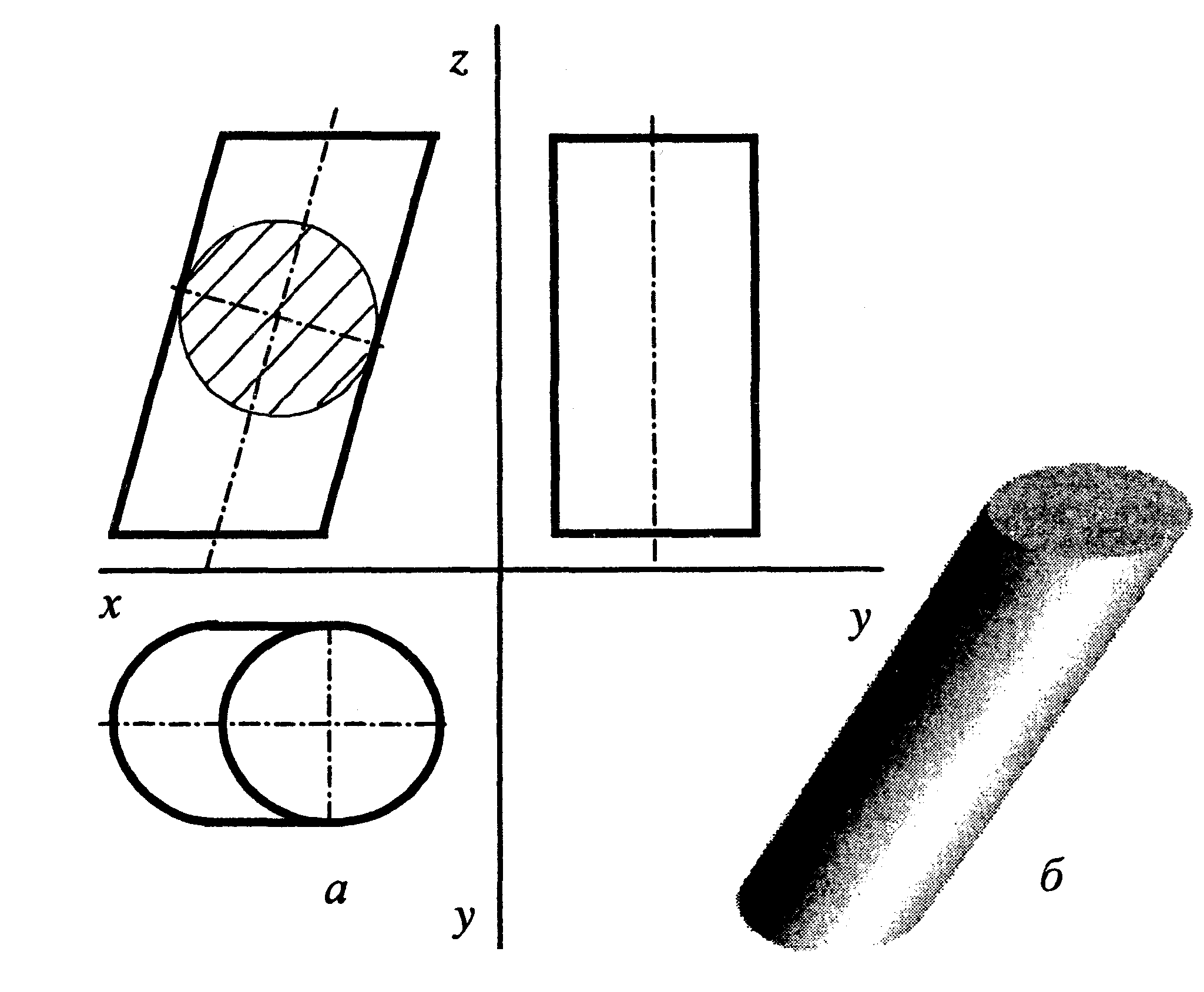

онус – геометрический объект, ограниченный конической поверхностью и плоскостью, называемой основанием или двумя плоскостями (усеченный конус). Конус может быть прямым (рис. 62) или наклонным.

Ш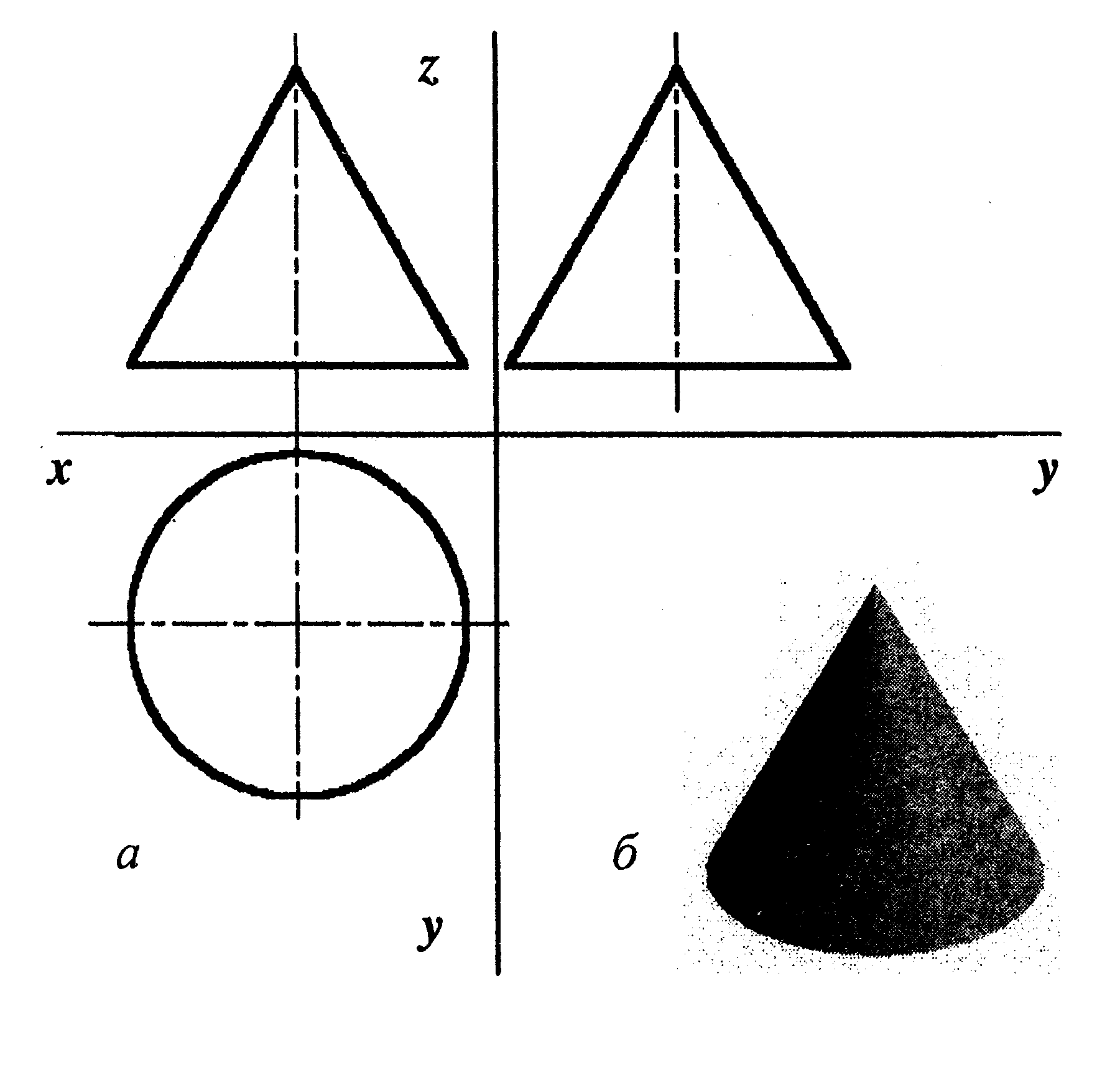 ар – геометрический объект, образованный вращением круга вокруг его диаметра (рис. 63). При сжатии или растяжении шар преобразуется в эллипсоид, который может быть получен вращением эллипса вокруг одной из осей: если вращение происходит вокруг большой оси, то эллипсоид называется вытянутым; если вокруг малой – сжатым, или сфероидом.

Т

Рис. 62. Прямой круговой конус: а) проекционный чертеж;

б) аксонометрия

ор – геометрический объект, образованный при вращении круга вокруг оси, не проходящей через его центр (рис. 64).

Рис. 63. Шар:

а) проекционный чертеж;

б) аксонометрия

Рис. 64. Тор:

а) проекционный чертеж;

б) аксонометрия