Команды работы со структурой матриц и векторов.
rowdim(M) число строк матрицы M.
coldim(M) число столбцов матрицы M.
vectdim(v) число элементов вектора v.
convert(list,vector) преобразование переменной типа list в вектор.
convert([list1,...,listn],matrix) преобразование набора переменных типа list в матрицу.
hilbert(n) создание Гильбертовой матрицы размерности nn.
addcol(M,i1,i2,expr) формирование новой матрицы, получаемой из матрицы M прибавлением к столбцу i2 столбца i1, умноженного на выражение expr.
addrow(M,i1,i2,expr) аналогична addcol, только для работы со строками матрицы M.
row(M,i) выделение i-ой строки из матрицы M.
col(M,i) выделение i-го столбца из матрицы M.
сoncat(M1,M2) cлияние матриц M1 и M2.
submatrix(M,i1..i2,j1..j2) выделение подматрицы из матрицы M со строками от i1 до i2 и столбцами от j1 до j2.
subvector(v,i..j) выделение подвектора из v с элементами v[i],...,v[j].
delrows(M,i..j) уничтожение столбцов с номерами от i до j у матрицы M.
delcols(M,i..j) уничтожение строк с номерами от i до j у матрицы M.
Поясним работу некоторых из перечисленных команд следующим примером:
#подключение пакета линейной алгебры
> with(linalg):
Warning: new definition for norm
Warning: new definition for trace
# задание матрицы M
> M:=matrix(3,3,[[1,2,3],[4,5,6],[7,8,9]]);
M:=
# вычисление определителя матрицы M
> det(M);
0
# вычисление ранга матрицы M
> rank(M);
2
# вычисление спектра матрицы M
> eigenvals(M);
# добавление 1 к диагональным элементам матрицы M
> M:=evalm(M+1);
M:=
# вычисление обратной к M матрицы
> evalm(1/M);
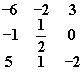
# задание вектора v с элементами x,y,z
>v:=array(1..3,[x,y,z]);
v:= [x y z]
# умножение матрицы M на вектор v
> u:=multiply(M,v);
u:=[2x+2y+3z 4x+6y+6z 7x+8y+10z]
# определение размерности вектора v
> vectdim(u);
3
# вычисление cкалярного произведения векторов v и u
> f:=dotprod(u,v);
f:=(2x+2y+3z)x+(4x+6y+6z)y+(7x+8y+10z)z
# вычисление дивергенции вектора u
> diverge(u,v);
18
# вычисление градиента функции f
> grad(f,v);
[4x+6y+10z 6x+12y+14z 10x+14y+20z]
# вычисление матрицы Якоби для вектора u по переменным v
> jacobian(u,v);
# вычисление характеристического многочлена для матрицы Якоби
> charpoly(",lambda);
# выделение подматрицы из матрицы M
> submatrix(M,2..3,1..3);
Программирование в среде Maple.
В пакете Maple для реализации алгоритмов и написания программ, существует набор основных конструкций аналогичный существующим в известных языках программирования ( например, язык PASCAL). Перечислим их.
Условный оператор
if bool1 then expr1 else expr2 fi
Эта конструкция дает возможность в зависимости от логического условия bool1 выполнять выражение expr1 (когда bool1=true), или выражение expr2 (bool1=false). Условный оператор должен быть закрыт при помощи служебного слова fi. Например:
> if 1/3<5/6 then 12/21 else 21/12 fi;
Расширенный вариант условного оператора имеет вид:
if bool1 then expr1 elif bool2 then expr2 ... elif booln then exprn else expr0 fi