Міністерство освіти і науки, молоді та спорту України

Донбаська державна машинобудівна академія (ДДМА)

СИСТЕМНИЙ АНАЛІЗ ПРЕДМЕТНОЇ ОБЛАСТІ

Методичні вказівки до лабораторних робіт

і контрольні завдання

для студентів спеціальності 7, 8.05010102

денної і заочної форм навчання

Краматорськ

ДДМА

2013

Міністерство освіти і науки, молоді та спорту України

Донбаська державна машинобудівна академія (ДДМА)

СИСТЕМНИЙ АНАЛІЗ ПРЕДМЕТНОЇ ОБЛАСТІ

Методичні вказівки до лабораторних робіт

і контрольні завдання

для студентів спеціальності 7, 8.05010102

денної і заочної форм навчання

Затверджено

на засіданні

методичної ради

Протокол № від

Краматорськ

ДДМА

2013

УДК 621.791

Системний аналіз предметної області. Методичні вказівки до лабораторних робіт і контрольні завдання для студентів спеціальності 7, 8.05010102 денної і заочної форми навчання) / уклад. : В. О. Паламарчук, С. О. Шевцов. – Краматорськ : ДДМА, 2013. – __ с.

Методичні вказівки містять короткі відомості з теоретичних питань, рекомендації з підготовки до виконання лабораторних робіт, вимоги до змісту та оформлення звіту, контрольні питання і літературу..

Укладачі: В. О. Паламарчук, доц.;

С. О. Шевцов, ст. викл.

Відп. за выпуск О. Ф. Тарасов, проф.

ВСТУП

Лабораторні роботи з дисципліни „Системний аналіз предметної області” складаються з теоретичних відомостей, індивідуальних завдань та запитань до самостійної підготовки, які дозволяють виробити практичні навички аналізу предметної області, вивчити математико-статистичні та фізичні методи моделювання на прикладах. Лабораторні роботи передбачають можливість розробки програм і використання відомих ППП для аналізу отриманих результатів.

Вимоги до виконання і оформлення лабораторних робіт:

Звіт з лабораторної роботи виконується на аркушах паперу формату А4 (з одного боку) і містить заголовок:

Лабораторна робота №___

З дисципліни „Системний аналіз предметної області”

Студента(ки) групи ІТ-___-____

Призвище та ініциали

Варіант _____

Текст звіту може бути друкований, або рукописний (змішаний). Кожна лабораторна робота починається з нової сторінки і закінчується чистим аркушем для роботи над помилками, або розв′язання завдань під час захисту. До захисту подається надійно зшита лабораторна робота. У кінці триместру, по закінченню вивчення дисципліни, усі лабораторні роботи з позначками захисту (включаючи кількість балів і підпис викладача) передаються викладачу для заліку усього курсу.

Звіт з лабораторної роботи повинен містити;

• назву роботи;

• мету роботи;

• індивідуальне завдання з конкретними значеннями параметрів виконуваного варіанту;

• стислі висновки за результатами виконання лабораторної роботи;

Якщо при виконанні лабораторної роботи виконувались елементи програмування, або використовувався існуючий ППП, то до звіту додається лістинг програми, роздруковка результатів роботи програми або ППП.

Лабораторна робота 3 створена на основі оригінальних матеріалів: статті [17] та програми обчислення, люб´язно наданих Грудкіною Н.С.

ЗМІСТ

ВСТУП…………………………………………………………………..

Лабораторна робота 1. Нечітка логіка і нечітка арифметика Теоретичні відомості...............................................................................

Завдання до лабораторної роботи……………………………………..

Зміст звіту……………………………………………………………….

Питання для контролю та самостійної роботи......................................

Лабораторна робота № 2 Представлення знань за допомогою фреймів...............................................................................................................

Теоретичні відомості...............................................................................

Завдання до лабораторної роботи……………………………………..

Зміст звіту……………………………………………………………….

Питання для контролю та самостійної роботи...................................

Лабораторна робота 3. Математичне моделювання заданої предметної області. Дослідження математичної моделі...........................

Теоретичні відомості...............................................................................

Завдання до лабораторної роботи……………………………………..

Порядок виконання роботи (етап 2)..................................................

Зміст звіту……………………………………………………………….

Питання для контролю та самостійної роботи...................................

Лабораторна робота 4. Математико-статистичні методи моделювання. Найпростіша обробка даних ................................................

Теоретичні відомості...............................................................................

Завдання до лабораторної роботи……………………………………..

Порядок виконання роботи..................................................................

Зміст звіту……………………………………………………………….

Питання для контролю та самостійної роботи...................................

Додаток 1. Розробка математичної моделі процесу комбінованого радіально-зворотного видавлювання деталей типу стакан з фланцем з використанням енергетичного методу верхньої оцінки [17]......................

Література...................................................................................................

Лабораторна робота 1.Нечітка логіка і нечітка арифметика.

Мета роботи: Вивчити особливості роботи з нечіткими множинами та з нечіткими числами.

Теоретичні відомості

Нечітка логіка – це математична наука, яка є розширенням класичної логіки і яка базується на концепції часткової істинності. Поняття нечітких множин (fuzzy sets) і нечіткої логіки (fuzzy logic) вперше запропонував американський вчений Лотфі Заде у 1965 р.

Основні переваги систем на основі нечіткої логіки:

• можливість оперувати значеннями, які неможливо задати однозначно, наприклад : „досить тепло”, „чоловік у розквіті сил” та ін..

• можливість формалізації нечітких критеріїв оцінки, таких як „переважно”, „можливо” та ін.

Нечітку множину задають двома елементами; базовими значеннями та функцією приналежності.

Нехай Х – деяка множина з елементами . Назвемо їх базовими значеннями. Кожному з цих елементів поставимо у відповідність функцію належності ( ), яка задає степінь належності кожного елемента до заданої нечіткої множини А.

(1.1)

Функцію належності ( або степінь належності - якщо це число, а не фукнція) задає користувач, виходячи з експериментальних даних, або з свого розуміння досліджуваного процеса.

Носієм нечіткої множини назвемо множину усіх , для яких . Якщо для усіх , то маємо справу зі звичайною, чіткою, множиною. Присвоювання елементам носія відповідних степенів належності називається фаззифікацією множини.

Чітка множина А^*, найближча до А, може бути задана таким чином:

(1.2)

Приклад 1. Задана нечітка множина А:

А={(1;0), (2;0,1), (3;0,4), (4;0,6), (5;1), (6;0,9), (7;0,7), (8;0,5), (9;0,3)}.

Знайти найближчу чітку множину А^*.

Відповідь: А^*={4,5,6,7,8}

Доповненням нечіткої множини є нечітка множина з таким самим носієм, але з функцією належності .

Приклад 2. Задана нечітка множина А:

А={(1;0), (2;0,1), (3;0,4), (4;0,6), (5;1), (6;0,9), (7;0,7), (8;0,5), (9;0,3)}.

Знайти доповнення - множину .

Відповідь:

= {(1;1), (2;0,9), (3;0,6), (4;0,4), (5;0), (6;0,1), (7;0,3), (8;0,5), (9;0,7)}.

Об′єднання та перетин нечітких множин можна виконувати різними способами. Найбільш уживаний – спосіб максиміну. Він використовується на нечітких множинах з однаковим носієм. Для перетину множин:

, (1.3)

а для об′єднання множин

. (1.4)

Приклад 3. Задані нечіткі ножини

А= {(пн;0,1), (вт;0,5), (ср;0,4), (чт;0), (пт;1), (сб;0,1), (нд;0,3)

В= {(пн;0,5), (вт;0,4), (ср;0,5), (чт;0,6), (пт;0,8), (сб;1), (нд;0,5)

Знайти перетин множин та об′єднання множин .

Відповідь:

={(пн;0,1), (вт;0,4), (ср;0,4), (чт;0), (пт;0,8), (сб;0,1), (нд;0,3);

= {(пн;0,5), (вт;0,5), (ср;0,5), (чт;0,6), (пт;1), (сб;1), (нд;0,5)

Елемент нечіткої множини А включений у нечітку множину В (обидві множини задані на одному носії) у тому випадку, якщо .

Приклад 4. Задані нечіткі множини

А= {(пн;0,1), (вт;0,5), (ср;0,4), (чт;0), (пт;1), (сб;0,1), (нд;0,3)

В= {(пн;0,5), (вт;0,4), (ср;0,5), (чт;0,6), (пт;0,8), (сб;1), (нд;0,5)

Знайти множину .

Відповідь: ={(пн;0,1), (ср;0,4), (чт;0), (сб;0,1), (нд;0,3)

Степінь включення множини А у множину В

(1.5)

Приклад 5 Знайти степінь включення множини А у множину В для приклада 4.

Відповідь:

Дефаззифікацію нечіткої множини будемо виконувати методом центра мас:

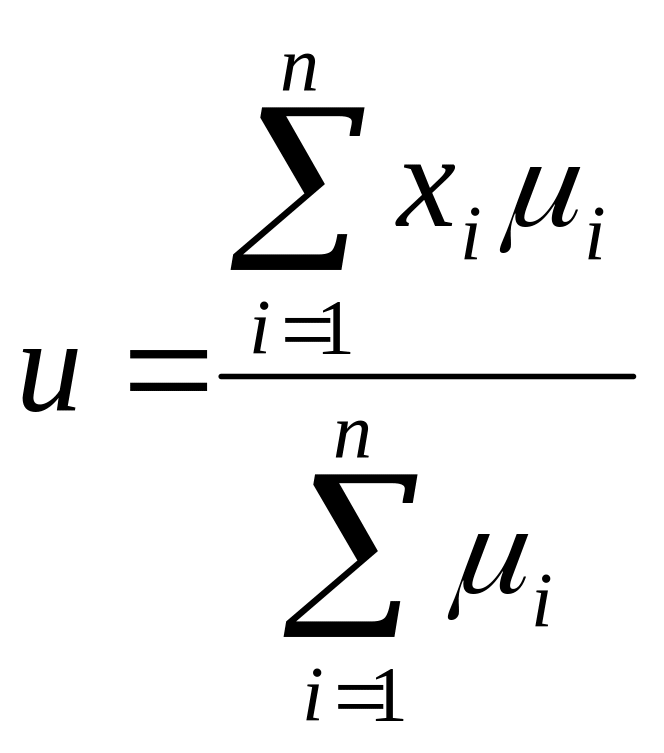. (1.6)

Приклад 6. Побудуємо нечітку множину: „чоловік середнього зросту”. Запишемо множину-носій:

Х={155; 160; 165; 170; 175; 180; 185; 190}

Методом експертної оцінки, або методом опитування, присвоємо цим показникам зросту відповідні степені належності.

А= {(155;0), (160;0,2), (165;0,5), (170;0,9), (175;1), (180;0,8), (185; 0,5), (190;0)}

Дефаззифікація цієї нечіткої множини дасть нам середній зріст „чоловіка середнього зросту”.

Відповідь:

Нечіткою відповідністю R множин X і Y є сукупність пар елементів, один з яких належить множині Х, а інший множині Y, і до кожної пари приєднана функція (степінь) приналежності. Іншими словами, нечітка відповідність є нечіткою підмножиною декартового добутку . Множину Х називають областю відправлення, а множину Y – множиною прибування нечіткої відповідності.

Приклад 7. Задамо деяку нечітку відповідність R, визначивши X і Y як , .

Граф нечіткої відповідності зображений на рис 1.1.

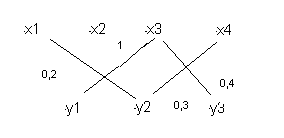
Рис. 1.1 Граф нечіткої відповідності

У матричному вигляді нечітка відповідність можна задати за допомогою матриці інциденцій

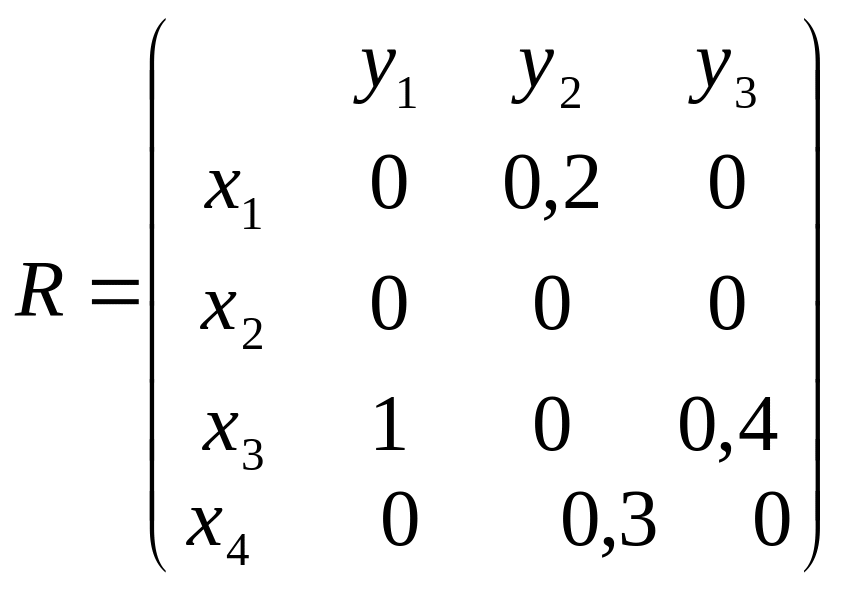(1.7)

Операції з нечіткими відповідностями виконують аналогічно операціям з нечіткими множинами, тобто за принципом максиміну.

Серед нечітких чисел найбільше розповсюдження мають нечіткі числа (L-R) типу. Арифметичні операції з такими числами є найбільш простими. Функції належності L(х) і R(х) таких чисел мають задовольняти умовам:

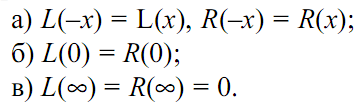(1.8)

Графіки таких функцій мають вигляд (рис. 1.2)

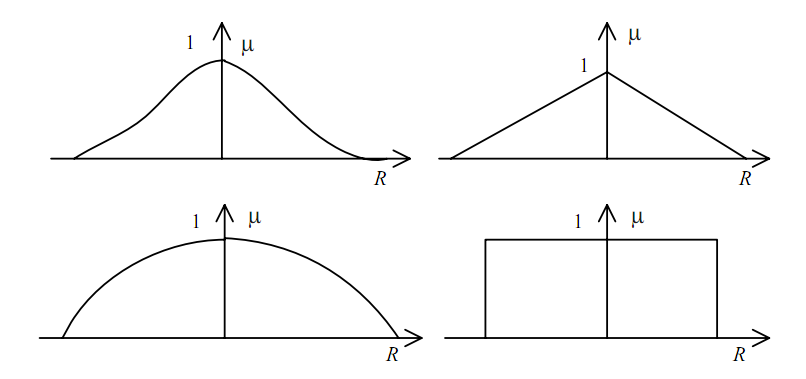
Рис. 1.2 L-R функції

Прикладами аналітичного задання функцій можуть бути

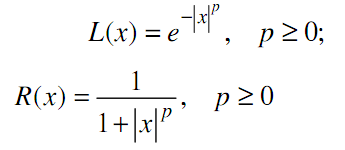(1.9)

Унімодальне число (L-R) типу задають трійкою (а, α, β). Тут а – є модою числа (μ(а)=1), α, β – лівий і правий коефіцієнти нечіткості.

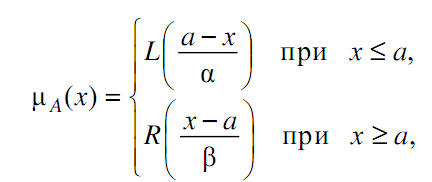(1.10)

Толерантне число (L-R) типу задають чотирма параметрами (а, b, α, β). Тут (а, b) – межі в яких μ(х)=1, а α, β – лівий і правий коефіцієнти нечіткості. Приклади графіків функцій належності нечітких чисел (L-R) типу наведені на рис. 1.3.

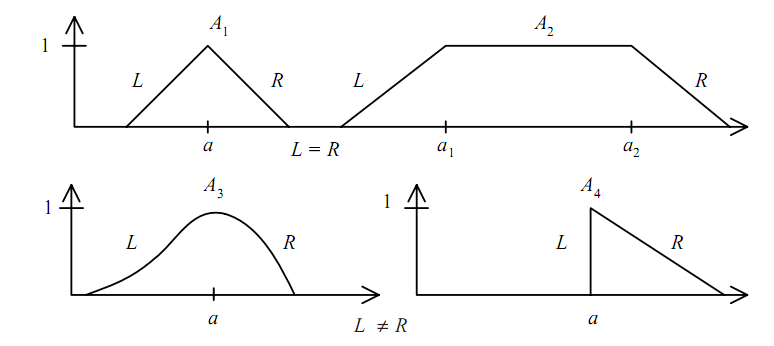
Рис. 1.3 Представлення нечітких чисел (L-R) типу

Арифметичні операції над нечіткими числами (L-R) типу мають такий вигляд:

• додавання

• віднімання

- множення

- ділення

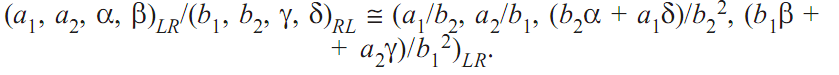
Для операцій max та min використовують такі наближені формули