1.6 Содержание отчета

1.Характеристика используемого прибора.

1.7 Контрольные вопросы

1.Описание прибора

2. Принцип работы

Лабораторная работа №3

ИЗМЕРЕНИЕ ПАРАМЕТРОВ КОЛЕБАТЕЛЬНОГО КОНТУРА

1.1 Цель работы

Определение параметров колебательного контура

2. Применяемая аппаратура

1. Генератор высокочастотных сигналов ГЧ-106 (ГВЧС);

2. Милливольтметр Ф-564 (мВ);

3. Мост переменного тока Р-577;

4. Макет схемы колебательного контура последовательного соединения.

1.3 Краткие сведения из теории

Важнейшей задачей любого радиоприёмника является выделение из большого числа высокочастотных колебаний, индуктируемых в антенне, только колебания нужной радиостанции. Это осуществляется при помощи колебательного контура. Он состоит из соединительных между собой конденсатора и катушки индуктивности.

1.3.1 Собственные колебания контура

Рассмотрим схему на рисунке 1.1. Когда ключ находится в положении 1, конденсатор заряжается от батареи. Если ключ переключить в положение 2, конденсатор начинает разряжаться через катушку индуктивности. Эта разрядка получается в результате того, что в контуре возникают синусоидальные электрические колебания определенной частоты (рисунок 1.2).

На рисунке 1.3 (а) показан первый момент этого процесса, когда напряжение на конденсаторе максимально, а ток начинает нарастать. В этот момент вся энергия, получаемая от батареи, сосредоточена между электродами конденсатора.

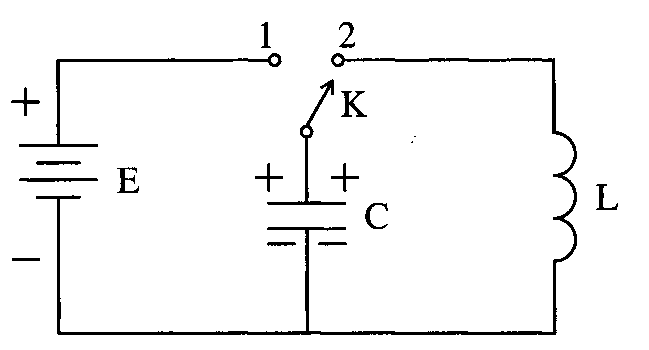
Рисунок 1.1 - Схема колебательного контура

На рисунке 1.3 (б) показан момент, когда ток достиг максимума, а конденсатора превратилась в магнитную энергию поля вокруг катушки индуктивности напряжение на конденсаторе равно нулю. Следовательно, энергия конденсатора превратилась в магнитную энергию поля вокруг катушки индуктивности. С этого момента ток начинает уменьшаться, и магнитные силовые линии начинают «собираться» к катушке и вызывают в ней ЭДС самоиндукции. Направление этой ЭДС таково, что оно «помогает» уменьшающемуся току.

Поэтому ток, вызванный «сужающимся» магнитным полем катушки индуктивности, продолжает протекать в том же направлении, заряжая снова конденсатор, но на этот раз с противоположной полярностью. Именно этот момент показан на рисунке 1.3 (в), когда конденсатор заряжен противоположной полярностью, и ток в цепи уже прекратился, т.е. магнитная энергия катушки индуктивности превратилась снова в электрическую энергию заряженного конденсатора.

В следующий момент конденсатор начинает снова разряжаться через катушку индуктивности. На рисунке 1.3 (г) он уже полностью разрядился, и ток максимален.

Далее магнитное поле опять «сужается» к катушке индуктивности и ток продолжает протекать в том же направлении, пока конденсатор снова не зарядится первоначальной полярностью (рисунок 1.3 (д )).

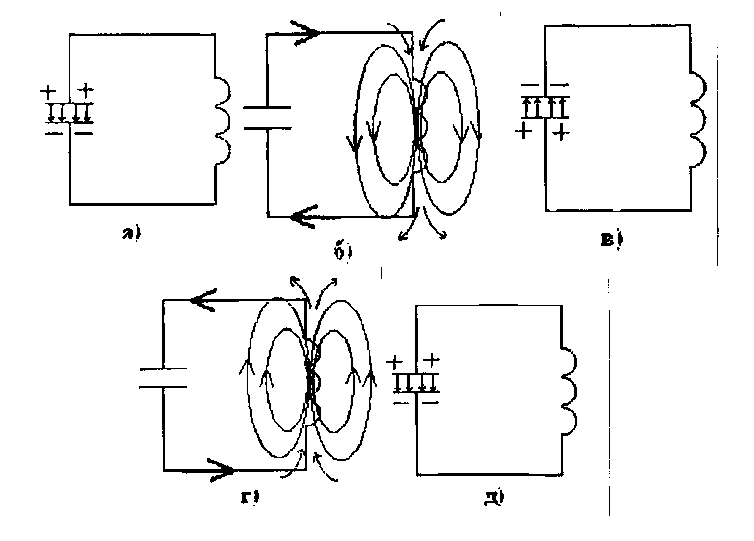
Рисунок 1.3 - Диаграммы возникновения электромагнитных колебаний

Описанные электрические колебания представляют собой контурный ток, изменяющийся по синусоидальному закону (рисунок 1.4).

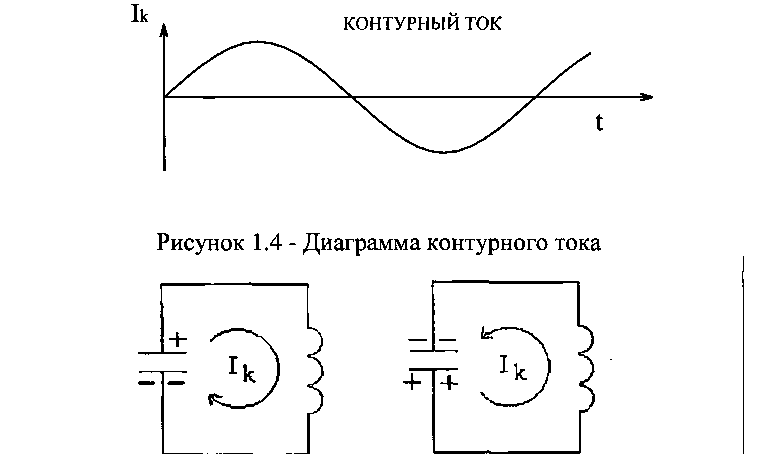
Рисунок 1.5 - Направление токов в колебательном контуре

В первый полупериод ток в колебательном контуре течет в одном направлении, а во втором полупериоде - в другом (рисунок 1.5). Ток здесь является результатом периодического превращения электрической энергии конденсатора в магнитную энергию катушки индуктивности и обратно.

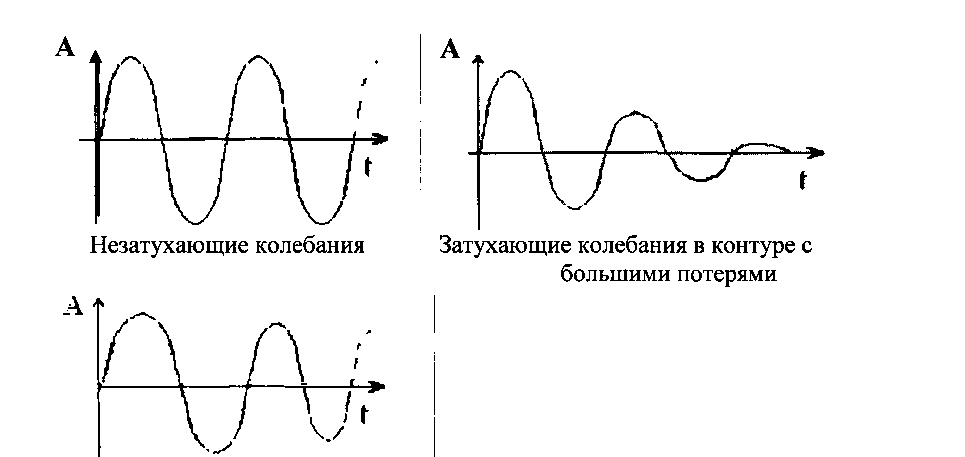
Затухающие колебания в контуре с малыми потерями

Рисунок 1.6 - Диаграммы колебаний

Если контур идеален (без потерь), то колебания будут незатухающими, т.е. будут продолжаться вечно. В реальных колебательных контурах колебания затухают тем быстрее, чем больше потерь имеет этот контур (рисунок 1.6).

1.3.2 Частота собственных колебаний контура

Частота возникающих колебаний (она же резонансная частота f_p ) зависит от емкости конденсатора и индуктивности катушки и вычисляется по формуле Томпсона:

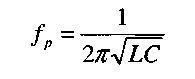
Из этой формулы следует, что чем меньше индуктивность и емкость, тем выше собственная частота контура и наоборот.

1.3.3 Электрический резонанс

На рисунке 1.7 показана схема опыта по электрическому резонансу. Здесь показан лабораторный генератор Г (сигнал-генератор), с помощью которого будем подавать высокочастотные колебания различной частоты, но всегда с напряжением 1мВ. Эти колебания подаются на колебательный контур LC посредством индуктивной связи между катушками L св и L.

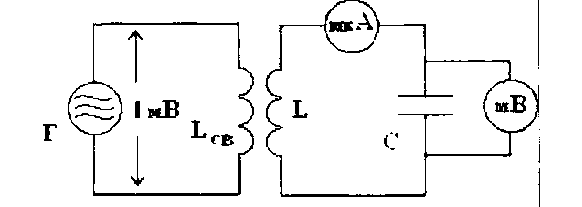
Рисунок 1.7 - Схема электрического резонанса

К контуру подключаются приборы для измерения контурного тока и напряжения на конденсаторе. Дадим L=200 мкГн и С=500пФ, частота собственных колебаний контура 500 кГц. На частоте 500 кГц контурный ток и напряжение на конденсаторе сильно нарастают, а на частотах выше и ниже 500 кГц быстро уменьшаются.

На рисунке 1.8 это явление изображено графически, а кривые называются частотными характеристиками колебательного контура. Посредством индуктивной связи в катушке L индуцируется переменная ЭДС, имеющая частоту генератора. В результате в контуре возникают так называемые вынужденные незатухающие электрические колебания (контурный ток) с частотой генератора. В принципе эти колебания имеют малую амплитуду, т.е. переменное напряжение на конденсаторе намного меньше напряжения генератора.

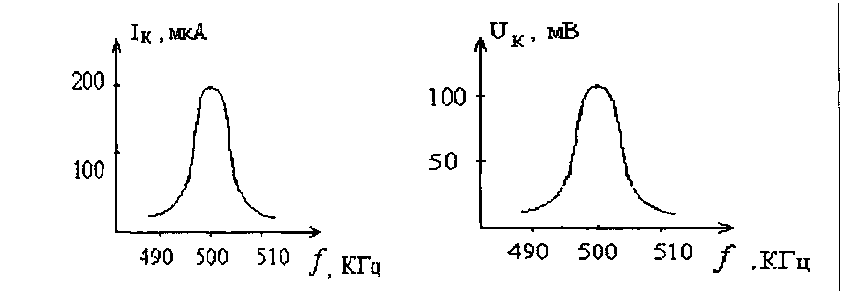
Рисунок 1.8 - Частотные характеристики колебательного контура

Когда частота генератора становится равной собственной частоте колебательного контура, наступает явление резонанса. Оно характеризуется тем, что контурный ток значителен, и напряжение на конденсаторе может стать во много раз больше (примерно в 120-150 раз) напряжения генератора. Следовательно, колебательный контур обладает так называемой частотной избирательностью и во время резонанса многократно увеличивает напряжение поданных на него колебаний.

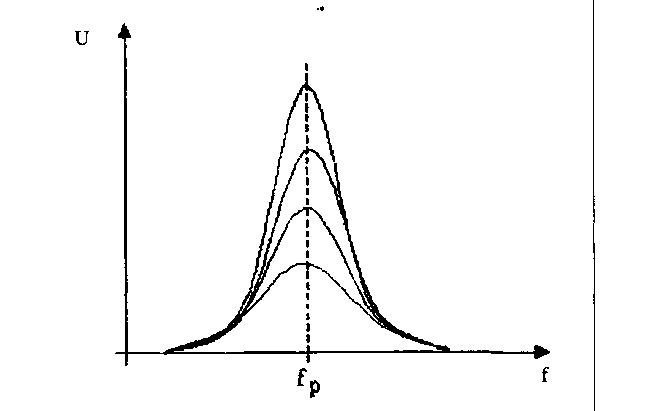
Чем больше добротность контура, тем больше выражены эти свойства (рисунок 1.9).

Рисунок 1.9 - Характеристики добротности контура

Следует отметить, что добротность контура зависит, прежде всего, от добротности катушки индуктивности, точнее от ее сопротивления потерь RnoT. Поэтому иногда реальные колебательные контуры изображаются вместе с сопротивлением потерь катушки индуктивности (рисунок 1.10).

идеальный колебательный реальный колебательный

контур контур

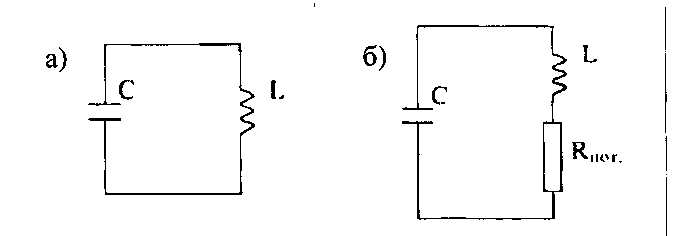
Рисунок 1.10 - Схемы колебательных контуров

Чем меньше Rnox, тем выше добротность контура. Хорошие колебательные контуры имеют добротность от 50 до 150.

а) идеальный колебательный контур имеет только емкость и индуктивность;

б) реальный колебательный контур имеет емкость, индуктивность и сопротивление потерь

1.3.4 Виды колебательных контуров

В электрических схемах колебательный контур связан (непосредственно, индуктивно, емкостной связью) с каким-либо источником электрических колебаний. Этим источником может быть антенна, усилительный каскад и пр., которые в общем случае являются генератором с определенным внутренним сопротивлением, частотой и амплитудой.

В зависимости от того, как соединен генератор с катушкой индуктивности и конденсатором, различают последовательный и параллельный колебательный контур.

Последовательный колебательный контур

В таком контуре генератор соединен последовательно с катушкой и конденсатором.

Во время резонанса последовательный контур характеризуется следующими особенностями:

• сопротивление контура минимально и равно Кпот;

• напряжение на конденсаторе (или катушке) в Q раз больше напряжения генератора. Здесь Q - добротность контура;

• ток, протекающий через контур, максимален и равен

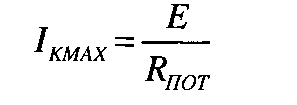
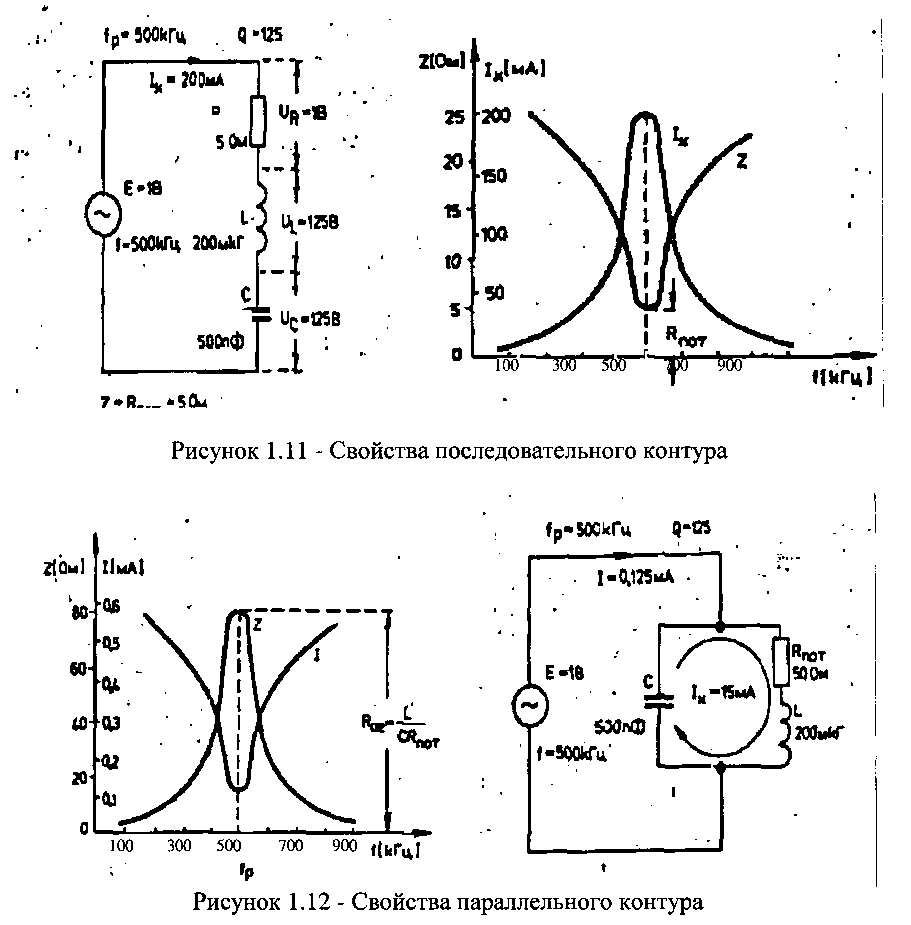
На рисунке 1.11. дан конкретный пример последовательного колебательного контура, а также и его частотные характеристики при условии, что внутреннее сопротивление генератора невелико.

Параллельный колебательный контур

В этом случае генератор соединен с катушкой индуктивности и конденсатором параллельно. При резонансе параллельный колебательный контур характеризуется следующими особенностями:

1. сопротивление контура велико и равно L/CRiiot. Это сопротивление иногда называется резонансным сопротивлением параллельно колебательного контура и обозначается Roe;

2. поскольку сопротивление контура большое, ток во внешней цепи сравнительно мал и равен E/Roe. Контурный ток сравнительно большой, он в Q раз больше тока во внешней цепи.

На рисунке 1.12 дан конкретный пример параллельного колебательного контура и его частотные характеристики, полученные при условии, что внутреннее сопротивление генератора большое.

Резонансная частота как последовательного, так и параллельного колебательного контура вычисляется по формуле Томпсона.

1. Выводы:

2. при разрядке конденсатора через катушку индуктивности получаются затухающие синусоидальные колебания, частота которых может быть найдена по формуле Томпсона;

3. в колебательном контуре могут быть возбуждены незатухающие колебания с помощью внешнего генератора. Если частота генератора совпадает с частотой собственных колебаний контура, наступает явление резонанс;

4. при резонансе сопротивление последовательного колебательного контура минимально, а напряжение на конденсаторе (или катушке индуктивности) напряжения генератора;

5. при резонансе сопротивление параллельного колебательного контура большое, а контурный ток в Q раз больше тока во внешней цепи;

6. резонансные свойства колебательного контура выражены тем ярче, чем выше его добротность.