Метод сопряженных направлений
Определение:
два
-мерных
вектора
и
называют сопряженными
по отношению к матрице
(или
-сопряженными),
если
скалярное произведение
,
при
.
Здесь
– симметрическая положительно
определенная матрица размером
.
Использование векторов, сопряженных относительно некоторой положительно определенной матрицы, составляет основу метода первого порядка, известного как метод сопряженных направлений.
Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции. Это существенно увеличивает скорость сходимости и позволяет, например, минимизировать квадратичную функцию с симметрической положительно определенной матрицей за конечное число шагов , равное числу переменных функции.
Метод
Флетчера-Ривса
решает эту проблему путем преобразования
на каждом шаге антиградиента
в
направление
,
-сопряженное
с ранее найденными направлениями
.
На первом направлении принимается:
(13)
Далее на каждом направлении ищется оптимальная точка:
(14)
Геометрический
смысл траектории спуска в методе
сопряженных градиентов показан на
рисунке. Из заданной начальной точки
осуществляется спуск в направлении
.
В точке
определяется вектор-градиент
.
Поскольку
является точкой минимума функции в
направлении
,
то
ортогонален вектору
.
Затем отыскивается вектор
,
-сопряженный
к
.
Далее отыскивается минимум функции
вдоль направления
и т. д.
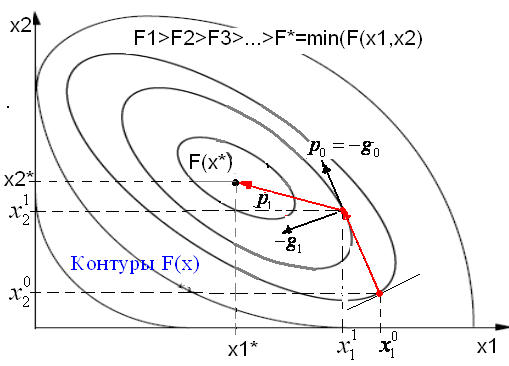
Методы сопряженных направлений являются одними из наиболее эффективных для решения задач минимизации.
Однако они чувствительны к ошибкам, возникающим в процессе счета. При большом числе переменных погрешность может настолько возрасти, что процесс придется повторять даже для квадратичной функции, т. е. процесс для нее не всегда укладывается в шагов.
Методы второго порядка
Методы
второго порядка допускают зависимость
в выражении
(5) от вторых частных производных
минимизируемой функции.
Свойства задачи минимизации методами второго порядка:
1)
Гессиан является симметричной
матрицей
;
2)
В окрестности точки минимума функция
может быть хорошо аппроксимирована
квадратичной формой
с положительно определенной матрицей.
Это значит, что Гессиан будет положительно
определен
;
3) В каждой точке пространства поисковых переменных известно направление (направление антиградиента), которое дает наискорейшее уменьшение функции.
Метод Ньютона
Классический
метод Ньютона соответствует
выбору
.
Так как
(матрица
Гессе является симметричной),
то
.
Отсюда,
. (15)
Метод Ньютона обеспечивает высокую скорость сходимости.
Однако существенным недостатком этого метода является необходимость на каждой итерации вычислять матрицу вторых производных минимизируемой функции.
Этого недостатка лишены квазиньютоновские методы.
Квазиньютоновские методы
Основной
идеей квазиньютоновских методов является
объединение
этапов сбора информации и поиска ее
минимума.
В этих методах, на основе информации о
значениях функции и ее производных в
точках поиска, строится некоторая
аппроксимация либо самого гессиана
либо обратного гессиана
(
– номер точки).
Формулы аппроксимирующие либо сам гессиан, либо обратный были выведены из условий:
|
|
|
|
|
|
(16)
В дальнейшем будем рассматривать матрицу аппроксимирующую обратный гессиан .
(17)
Где
– матрица, найденная по какому либо
алгоритму. При выводе аппроксимирующей
формулы предполагалось, что матрица
полученная на
-ой
итерации обладает некоторыми положительными
свойствами, к примеру, хорошо аппроксимирует
обратный Гессиан
.
Поэтому искомая матрица
должна минимально отличаться от матрицы
.
Таким образом, выражение для матрицы
было найдено из условия наименьшего
изменения матрицы
.
При этом было выполнено требование,
чтобы приближение
к матрице
,
удовлетворяло условию:
(18)
где
,
.
Методы, удовлетворяющие условию (16), называются квазиньютоновскими методами 1-го рода.
Наибольшее распространение получили формулы:
Давидона-Флетчера-Пауэлла (DFP)
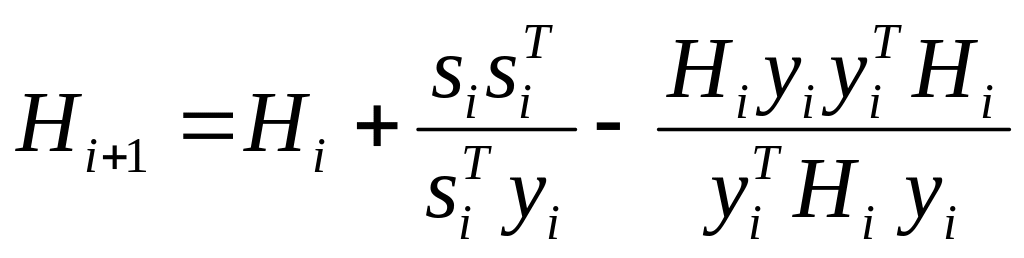(19)
Бройдена-Флетчера-Гольдфарба-Шенно (BFGS)
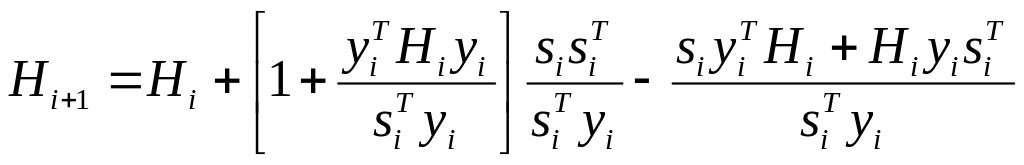(20)
В методах второго порядка, как и в методах первого порядка, градиент целевой функции вычисляется аналитически, либо с использованием разностей (12).
Общее правило выбора метода оптимизации
«Чем больше информации о производных, которую можно получить ценой приемлемых затрат, будет использовано при решении задачи, тем лучше». Ф.Гилл, У.Мюррей, М.Райт Практическая оптимизация, - М.: Мир, 1985