
- •Теория нелинейных систем автоматического управления
- •Фазовая траектория системы, изображенная на фазовой плоскости, соответствует:
- •Корни характеристического уравнения системы, изображенные на комплексной плоскости:
- •3.Корни характеристического уравнения системы, изображенные на комплексной плоскости:
- •5 Корни характеристического уравнения системы, изображенные на комплексной плоскости:
- •Фазовая траектория системы, изображенная на фазовой плоскости, соответствует:
- •11. Определите функцию
Корни характеристического уравнения системы, изображенные на комплексной плоскости:
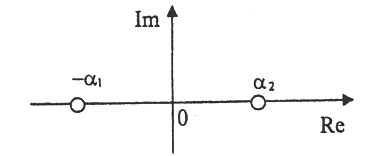
соответствуют:
А) особой точке типа устойчивый фокус
В) особой точке типа центр
С) особой точке типа седло
D) дифференциальному уравнению второго порядка
Е) 0
F) экспоненциально расходящемуся процессу
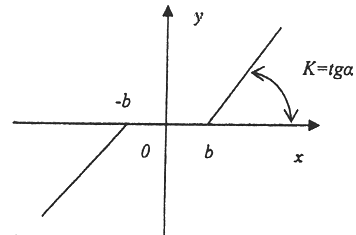
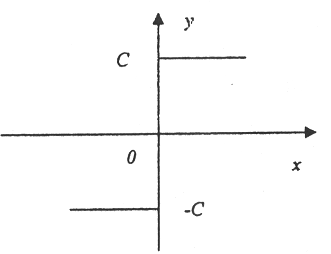
2.Типовая характеристика нелинейного звена системы с входным х(t) и выходным у(t) сигналами, соответствует выражению:
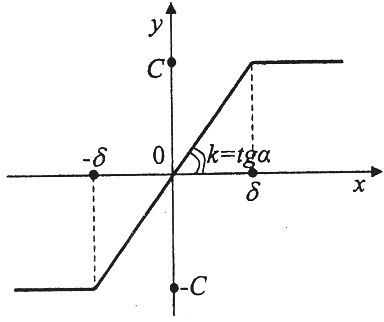
A) линейное звено
В) идеальное реле
С) звено с динамической нелинейностью
D) усилитель с зоной нечувствительности
Е) нелинейное звено
3.Корни характеристического уравнения системы, изображенные на комплексной плоскости:
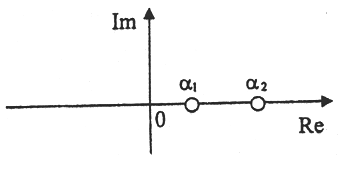
соответствуют:
A)особой точке типа устойчивый узел
B)особой точке типа неустойчивый узел
C)экспоненциально расходящемуся процессу
D) особой точке типа устойчивый фокус
Е) особой точке типа седло
F) 0
4.Определите корни характеристического уравнения системы, соответствующие особой точке фазовой плоскости типа центр:
Чисто мнимые корни
Корни, лежащие на мнимой оси комплексной плоскости
Положительное и отрицательное вещественное число
Комплексно-сопряженное число с положительной вещественной частью
Отрицательные вещественные числа
5 Корни характеристического уравнения системы, изображенные на комплексной плоскости:
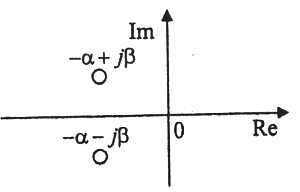
соответствуют:
A) особой точке типа устойчивый фокус
B) особой точке типа центр
C) особой точке типа седло
D) экспоненциально сходящемуся колебательному процессу
E) экспоненциально расходящемуся процессу
Определите корни характеристического уравнения системы, соответствующие следующему фазовому портрету:
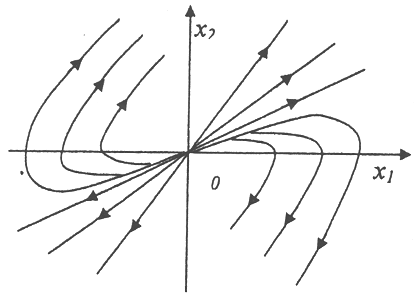
A) отрицательные вещественные числа
В)
C)
D)
E) Корни, лежащие на действительной отрицательной полуоси комплексной плоскости
F) Положительные вещественные числа
7. Приведите основные понятия метода фазовой плоскости в соответствии с рисунком:
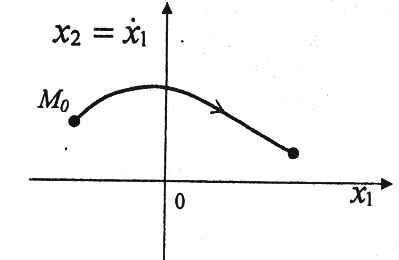
Фазовое пространство
импульсная характеристика
переходной процесс
изображающая точка М0
фазовая плоскость
Фазовая траектория системы, изображенная на фазовой плоскости, соответствует:
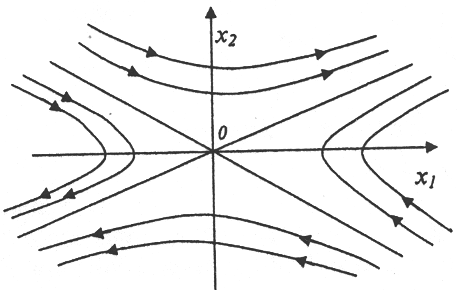
A) особой точке типа седло
расходящемуся временному процессу
0
D) экспоненциально сходящемуся процессу
Е) особой точке типа неустойчивый узел
F) колебательному процессу с постоянной амплитудой и частотой
Определите функцию

Отрицательная знакопостоянная функция
Положительная знакоопределенная функция

Отрицательная знакоопределенная функция
Е) Функция сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства
10.Задана
нелинейная система с нелинейным элементом
(где х
= аsіп
t):
и
линейным звеном с передаточной функцией,
 тогда
на основе критерия Гольдфарба:
тогда
на основе критерия Гольдфарба:
Годограф гармонически линеаризованного нелинейного звена:

Частотная передаточная функция линейной части:

Частотная передаточная функция линейной части:

Годограф гармонически линеаризованного нелинейного звена:

Е) Годограф гармонически линеаризованного нелинейного звена:
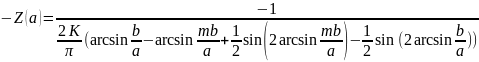
11. Определите функцию
Функция во всех точках n-мерного пространства, исключая начало координат, сохраняет один и тот же знак и нигде не обращается в нуль, кроме самого начала координат
Функция в данной области вокруг начала координат может иметь разные знаки
О) Знакопостоянная функция
Е) Функция сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках пространства
Следующий фазовый портрет системы соответствует:
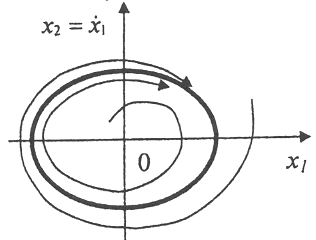
неустойчивый предельный цикл
устойчивый предельный цикл
0
D) двум точкам равновесия - особым точкам типа неустойчивый и неустойчивый узел
Е) двум точкам равновесия - особым точкам типа седло и центр
F) особой линии предельный цикл
С) особой точке центр
Фазовая траектория нелинейной системы
 :
:
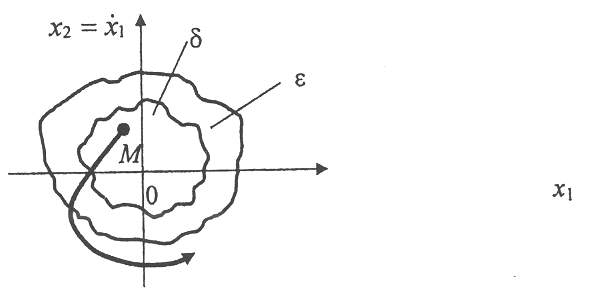
соответствует понятию:
неустойчивости по Ляпунову невозмущенного движения
асимптотической устойчивости системы в целом
глобальной асимптотической устойчивости невозмущенного движения системы
D) 0
Е) абсолютной устойчивости
Ғ) устойчивости невозмущенного движения системы
Определите отрицательную знакоопределенную функцию V(х1,х2):
A) V(х1,х2)= -(4 +4 )
B) V(х1,х2) = х1 +х2
C)V(х1,х2) = + 2x1x2+
D) V(х1,х2)=(x1+x2)2
E) V(х1,х2) = - -
Ғ) V(х1,х2) = -(x1+x2)2
15 Для исследования устойчивости системы выбрана функция Ляпунова:
V(x1,x2)=3
В соответствии с системой производная от функции Ляпунова:
(x1,x2)
= -(6 )2
тогда:
)2
тогда:
Функция Ляпунова положительная знакопостоянная
Функция Ляпунова отрицательная знакопостоянная
Производная от функции Ляпунова - отрицательная знакоопределенная
Система неустойчива в соответствии со вторым методом Ляпунова
Производная от функции Ляпунова - отрицательная знакопостоянная
Функция Ляпунова отрицательная знакоопределенная
16
Для исследования устойчивости системы
выбрана функция Ляпунова: V(х1,х2)=
В соответствии с системой производная от функции Ляпунова:
(x1,x2)= (6 )2
тогда:
Функция Ляпунова отрицательная знакоопределенная
Система неустойчива в соответствии со вторым методом Ляпунова
Функция Ляпунова отрицательная знакопостоянная
Производная от функции Ляпунова - положительная знакопостоянная
Функция Ляпунова положительная знакопостоянная
Система устойчива в соответствии со вторым методом Ляпунова
Функция Ляпунова положительная знакоопределенная
Дискретная система управления описывается уравнением, связывающим входной, и, и выходной, у, сигналы :
A)

B) y(k+2)+5y(k+1)+6y(k)=2u(k)
C) 6y(k)=2u(k)
D)
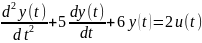
E)

F) 5y(k+1)+6y(k)=2u(k)
G)

Задана нелинейная система с нелинейным элементом (где X =
 ):
):
и
линейным звеном с передаточной функцией
 тогда
тогда
передаточная функция разомкнутой системы: W(S)=

характеристический полином замкнутой системы: D(s)=s)1+T1s)(1+T2s)+K

С) передаточная
функция разомкнутой системы: W(S)=
Б)
передаточная функция замкнутой системы:
W(S)=
E)
передаточная функция замкнутой системы
W(S)=
Пусть задана дискретная передаточная функция:
W(z)=
тогда:
характеристическое уравнение: 0.5z + 0.2 = 0
в соответствии с корнями характеристического уравнения импульсная система устойчива
в соответствии с корнями характеристического уравнения импульсная система неустойчива
Б) характеристическое уравнение: z2-0.2z+0.05=0
Е)
полюса передаточной функции: z1,2=0,1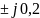
Задана нелинейная система с нелинейным элементом (где x=asin


и
линейным звеном с передаточной функцией,

тогда на основе критерия Гольдфарба:
Частотная передаточная функция линейной части:

Годограф гармонически линеаризованного нелинейного
звена:-Z(а)
=

Годограф гармонически линеаризованного нелинейного звена:
-Z(а)=-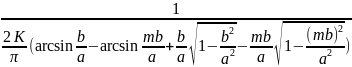
Частотная передаточная функция нелинейного звена:
Wн( )=
)=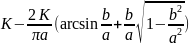
Частотная передаточная функция нелинейного звена:
Wн(
)=
Ғ) Частотная передаточная функция линейной части:

В соответствии с теоремой Ляпунова об устойчивости, производная от функции Ляпунова V(x1,x2)= нелинейной системы

соответствует выражению:
Знакопеременная функция
Отрицательная знакопостоянная функция

Отрицательная знакоопределенная функция
 2
2 2
2
Задана нелинейная система с нелинейным элементом (где х = asin
 ):
):
 ,
,
 ,
,
и линейным звеном с передаточной функцией, Wл(S)= тогда:
Частотная передаточная функция нелинейного звена:
Wн( =
=
Частотная передаточная функция нелинейного звена:
Wн(
=
C) Годограф гармонически линеаризованного нелинейного звена:-Z(a)=-
D) Годограф гармонически линеаризованного нелинейного звена:
-Z(а)
=
Е) Частотная передаточная функция линейной части:
Wл(
=
F)Годограф гармонически линеаризованного нелинейного
звена:-Z(а) = -
Частотная передаточная функция нелинейного звена: Wн( =
В соответствии с теоремой Ляпунова о неустойчивости, производная от функции Ляпунова V(х1,х2) = нелинейной системы

соответствует выражению:

Знакопеременная функция
Положительная знакоопределенная функция

Отрицательная знакопостоянная функция
Положительная знакопостоянная функция
Отрицательная знакоопределенная функция
24.
В соответствии с теоремой Ляпунова о
неустойчивости, производная от функции
Ляпунова V(х1,х2)
=
+ нелинейной системы
нелинейной системы
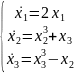
соответствует выражению:
Положительная знакопостоянная функция
Положительная знакоопределенная функция
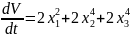
D)
Е) Знакопеременная функция
Ғ) Отрицательная знакопостоянная функция
Задана нелинейная система с нелинейным элементом (где х = 4sin ):
и линейным звеном с передаточной функцией, Wл(s)=
тогда на основе критерия Гольдфарба:
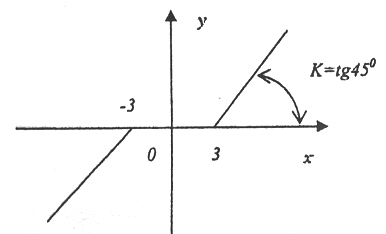
Частотная передаточная функция нелинейного звена: Wн( )=

Годограф гармонически линеаризованного нелинейного звена:
-Z(a)=
-
Частотная передаточная функция нелинейного звена:
Wн(
)=
Частотная передаточная функция линейной части:
Wл(
)=
Е) Частотная передаточная функция нелинейного звена:
Wн(
)= Ғ)
Годограф гармонически линеаризованного
нелинейного
звена:-Z(а)
= -
Ғ)
Годограф гармонически линеаризованного
нелинейного
звена:-Z(а)
= -

G)Годограф гармонически линеаризованного нелинейного звена:
-Z(a)=-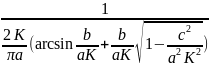
***************************************************************
