Интегралдау әдісі. Бастапқы параметрлер әдісі.
Июші моменттің таңбасы координата осьтерінің бағытына тәуелсіз, ал теңдіктің сол жағындағы екінші туындынын таңбасы тәуелді. Егер иілген осьтің ойыс жагы Ү осінің оң бағытымен сәйкес келсе, екінші туынды оң, ал дөңес жағы сәйкес келсе, теріс таңбалы болады (1-сурет). Серпімділік сызықтың теңдеуін бір рет интегралдап, көлденен қималардың бұрылу бұрыштарының (у' = Ө) теңдеуін аламыз
ЕІf'
= ЕІх
=
М(z)dz
+ С,
(8.6)
мұндағы С — интегралдау тұрақтысы.
Бұрылу бұрышы деп қиманың күш әсеріне дейінгі бұрылмаған жазықтығы мен күш әсерінен кейінгі бұрылған жазықтығының арасындағы бұрышты айтады. Қималардың сағат тілінің бағытына қарсы бағытта бұрылу бұрышы оң, ал сағат тілі бағыты бойымен бұрылу бұрышы теріс таңбалы деп қарастырылады.
Серпімділік сызығының теңдеуін екі рет интегралдап, арқалықтың кез келген қима тұсындағы иілу мөлшерін -у өрнектейтін тендеуді аламыз:
ЕІf = dz M(z)dz + Сz + D (8.7)
мұндағы – D екінші интегралдау тұрақтысы.
Иілу мөлшері деп, қима ауырлық центрінің бойлық оське перпендикуляр бағытта (У осіне параллель) төмен – жоғары орын ауыстыру шамасын айтады. Ауырлық центрі абсцисса осінен жоғары қарай орын ауыстырса иілу мөлшері оң, ал төмен қарай орын ауыстырса теріс таңбалы деп қарастырылады.
Алынған теңдеулердегі тұрақты шамалар (С, D) арқалықтың бекіту шарттарынан анықталады. Тұрақты шамалар белгілі болса, (8.5, 8.6) теңдіктерін пайдаланып, кез келген қиманың бұрылу бұрышы мен иілу мөлшерін анықтауға болады.
Кез келген күш түсірілген сырықтың потенциялық энергиясы
Потенциялық энергияның анықталуы бруста пайда болатын ішкі күш әсерлерін талдаудан туындайды. Бұл талдау қималар әдісімен жүргізіледі де, июші және бұраушы моменттерінің эпюрлерін, ал қажет жағдайда тік және көлденең күш эпюрлерін салумен анықталады
Барлық жағдайда ішкі күш әсерлерінің эпюрлерінің эпюрлері брустың осьтік сызығына салынады. Ал, күш әсерінің шамасы 9.1- суретте көрсетілгендей тегеурін нормаль бойынша оське салынады. Кеңістік брус үшін ось сызығы, әдетте, перспективада сызылады және бұраушы, июші моменттердің эпюрлері бейнеленеді (9.2 – сурет).
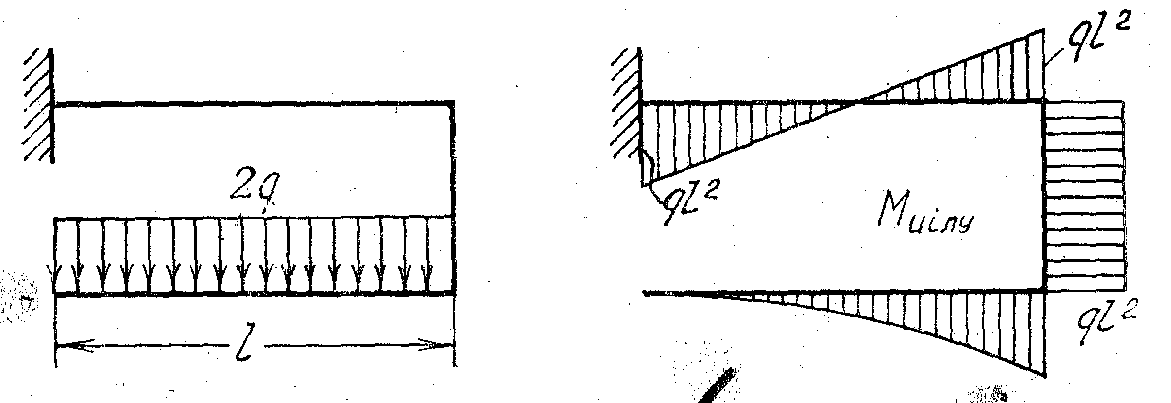
9.1- сурет
Потенциялық энергияны анықтау үшін брустан ұзындығы dz элеметтер учаскені бөліп алайық Брус тік және бастапқы қисықтығы кіші түрде болуы мүмкін. Күш түсірілген жалпы жағдайда әрбір көлденең қимада алты әсер: үш момент және күш пайда болады. Бөліп алынған учаскеге қатысты осы күш әсерлерін сыртқы күштер деп санап, олардың элементті деформациялау кезінде істеген жұмысын анықтаймыз. Бұл жұмыс брустың элементтер учаскесінде жинақталған потенциялық энергияға тең болады.
Сол жаққа түсірілген барлық күш әсерінің жұмысы нөлге тең болуы үшін элементтің сол қимасын шартты түрде қозғалмайтын деп қарастырамыз. Оң қиманың күш түсірілген нүктесі элементтің деформациясы салдарынан шамалы орын ауыстырып, іздеп отырған жұмыс стелінеді. Алты күш әсеріне жеке – жеке сәйкес келетін орын ауыстыру кезінде қалған бес әсердің біреуі де жұмыс істемейтіндей болуының үлкен маңызы бар.
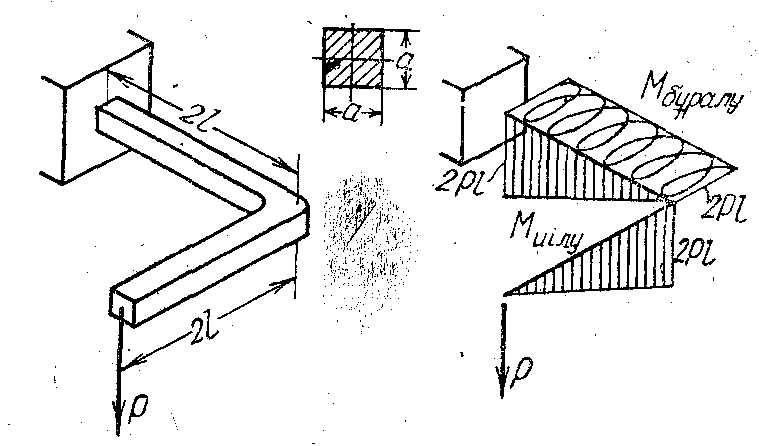
9.2- сурет
Мысалы,
моменті
әсерінен z осіне сәйкес қиманың бұралу
бұрышы пайда болады. Осы бұрыштық орын
ауыстыруда жұмыс тек
моментімен
істелінеді. Y осі бойынша сызықтық орын
ауыстыру
күш әсерінен болады да, орын ауыстыру
кезінде тек осы күш жұмыс атқарады.
Демек, элементтің потенциялық энергиясы
алты күш әсерінің әрқайсысының атқарған
тәуелсіз жұмыстарының қосындысы, яғни
бұралу, иілу, созылу және ығысу
энергияларының қосындысы ретінде
қарастыруға болады:
(9.1)
Алғашқы төрт қосылғыш өрнектері бізге белгілі:
;
;
;
.
Тек
және
ығысу энергиясын табу қажет.
шамасын анықтау үшін табан ауданы dF
және ұзындығы dz болатын элементар
призманы қарастырамыз (8.4-сурет). Бұл
көлемдегі энергия
dz тең, мұндағы
-
ығысу кезіндегі меншікті потенциялық
энергия:
.
Сонымен,
dFdz. F аудан бойынша интегралдасақ:
Журавский
формуласы (7.12) бойынша
.
Демек,
,
немесе
;
(9.2)
деп
белгілейік. Сонда
,
осыған ұқсас
.
және
коэффицеттері
қиманың геометриялық түріне байланысты
өлшемсіз шамалар.
Түрлендіріп
(9.2) формуласы бойынша
.
Тұтас дөңгелек қима үшін
.
Жұқа қабырғалы дөңгелекпрофиль үшін
R=2 және т.с.с. Енді (9.1) өрнегі мынадай
түрде болады:
.
Брустың потенциялық энергиясын алу үшін бұл өрнекті брустың ұзындығы бойынша интегралдау керек:
(9.3)
Егер конструкция күрделі болып, ол брус тәрізді бірнеше элементтерден құралса, онда интегралдаудан кейін әр брус шегінде құраушы элементтер санына сәйкес энергияларды қосу қажет болады.
(9.3) өрнектегі барлық қосылғыштар тең болмайды. Практикада кездесетін көптеген жүйелерде құраушы элементтер иілу не бұралу жұмысын атқарса, (9.3) өрнегіндегі соңғы үш қосылғыш алғашқы үшеуіне қарағанда айтарлықтай аз болады. Басқаша айтқанда, созылу және ығысу энергиясы, әдетте иілу және бұралу энергиясынан аз болады. Бірақ, сонымен бірге қосылғыштардың шамалары бірдей болуы ықтимал.