4.3. Статический расчет рамы

Поскольку рама является один раз статически неопределимой системой, то определяем значение лишнего неизвестного, которым является продоль­ное усилие в ригеле "F_x". Расчет выполняем для каждого вида загружения:

— от ветровой нагрузки на стены:

F_x,w,1= -(Q_d,w,1+Q¹_d,w,1)×p³×(4×H-p)/(16×H³)=-(1,17-0,73)х5³х(4х9,4-5)/(16х9,4³)= -0,13 кН

где р=5 м - принято для удобства расчёта загружения ветровой на­грузкой ;

F_x,w,2 = -(Q_d,w,2+Q¹_d,w,2) ×(p⁴+3×H⁴-4×p³×H)/(16×H³)= -(1,32-0,83)х(5⁴+3х9,4⁴-4x

x5³х9,4)/(16х9,4³)= - 0,71 кН;

— от ветровой нагрузки, приложенной в уровне ригеля:

F_x,w,3 = -(Q_d,w,3+Q¹_d,w,3) /2 = - (-9,26-9,26)/2=9,26 кН;

— от стенового ограждения:

F_x,ст =-9×M_ст/(8×H) = -9x(-16,39)/(8x9,4)=1,96 кН,

где M_ст=F_d^ст×e = -32,78 х 0,5= -16,39 кНм,

здесь e=0,5x(h_n+h)=0,5x(0,8+0,2)=0,5м - расстояние между се­рединой колонны и стенового ограждения, толщина стенового ограждения принята равной высоте сечения деревянной со­ставляющей покрытия.

Примем, что положительное значение неизвестного "F_x" направлено от узлов рамы, а изгибающего момента - по часовой стрелке.

Определим изгибающие моменты в заделке рамы.

Для левой колонны:

M_d,л = ((Q_d,w,3+F_x,w,1+F_x,w,2+F_x,w,3)×H+Q_d,w,1×p²/2+Q_d,w,2×((H-p)×(H+p)/2)×ψ₂+F_x,ст×H+M_ст )=

=[(-9,26-0,13-0,71+9,26)х9,4+1,17х5²/2+1,32х[(9,4-5)х(9,4+5)/2]х0,9+1,96 х

x9,4-16,39=46,40 кНм,

Для правой колонны:

М_d,пр = ((Q¹_d,w,3+F_x,w,1+F_x,w,2+F_x,w,3)×H+Q¹_d,w,1×p²/2+Q¹_d,w,2×((H-p)×(H+p)/2)×ψ₂+F_x,ст×H× M_ст)

=((-9,26-0,13-0,71+9,26)×9,4-0,73х5²/2-0,83х[(9,4-5)х(9,4+5)/2]х0,9+1,96 х

x9,4-16.39= -38,65 кНм.

Поперечная сила в заделке:

V_d,л = (Q_d,w,3+F_x,w,1+F_x,w,2+F_x,w,3)+Q_d,w,1×p+Q_d,w,2×(H-p))×ψ₂+F_x,ст =

=[-9,26-0,13-0,71+9,26)+1,17х5+1,32×(9,4-5)]х0,9+1,96 =12,20кН;

V_d,пр = (Q¹_d,w,3+F_x,w,1+F_x,w,2+F_x,w,3)+Q¹_d,w,1×p+Q¹_d,w,2×(H-p))×ψ₂+F_x,ст =

=((-9,26-0,13-0,71+9,26)-0,73х5-0,83х(9,4-5))х0,9+1,96 = -5,82 кН,

Расчетные усилия: M_d=M_d,_л=46,40 кНхм; V_d=V_d,_л=12,20 кН;

N_d =F_d^пок+F_d^ст+F_d^кол+F_d^сн×ψ₂ =44,95+32,78+92,26+22,15х0,9=189,93 кH,

где ψ₂=0,9 - коэффициент сочетания, учитываю­щий действие двух кратковременных нагрузок.

4.4 Подбор сечения колонны

Т.к. Н=9,4 м - отметка низа стропильных конструкций, то определим расчётную длину колонны по формуле:

H_к = H - h_об= 9,4 - 0,1=9,3 м,

где h_об ≥ В/(0,289×λ_max)=550/(0,289x200)=9,51 см,

принимаем h_o6=10,0 см. - высота сечения обвязочного бруса из условия устойчивости(п. 5.3.1.15, прил Б, табл Б.1 [1])

здесь В=5,5 м - шаг несущих конструкций;

λ_max=200 - предельная гибкость для связей.

Проектируем колонну прямоугольного сечения. Ширину се­чения определяем (b≥100 мм) из условия предельной гибкости из плос­кости рамы с учётом установки распорки по середине высоты колонны.

b_тр = (H_к/2)/(0,289×λ_max) =(940/2)/(0,289х120)=13,55см,

где l_у=Н_к/2 - расчетная длина колонны из плоскости рамы с учётом установки распорки по середине высоты колонны;

λ_max=120 - предельная гибкость колонны .

Принимаем ширину сечения b=200 мм.

Рисунок 4.3― Сечение колонны

После назначения ширины сечения колонны надо проверить длину опорной плиты фермы l_пл по формуле:

l_пл=b+2х(а_уг+1,5хd_от)=20,0+2х(3,0+1,5x1,5)=25,50 см,

где b=20см - ширина сечения колонны;

a_ys=3,0 см - расстояние от края элемента крепления (уголка) до центра отверстия под болт;

d_om=1,5 см - предварительно принятый диаметр отверстия под болт, крепящий ферму к колонне.

Высоту сечения колонны принимаем из 16 досок толщиной 40мм (после острожки). Тогда высота сечения h=16x40=640 мм.

Геометрические характеристики сечения:

A_d=20x64=1280 см², W_d=20x64²/6=13653см³,

Моменты инерции сечения.

I_z,sup= 20х64³/12=436907 см⁴, I_y,sup= 64x20³/12=42667см⁴.

где А– площадь опорного сечения

Момент сопротивления принятого сечения:

W_d=2·I_z,sup/h=2·436907/64=13653 см³,

Проверим сечение сжато-изогнутого элемента по формуле (7.31) [1] (см. п. 6.3.1).

Таким образом: l_d,z = μ₀×l_z =2,2× 930=2046 см,

где μ_o=2.2 - при одном защемлённом и втором свободном конце стержня (табл. 7.1 [1]).

см;

λ_z=I_d,z/i_z=2046/18,46=110,83 < λ_max=120 (табл. 7.2 [1]);

;

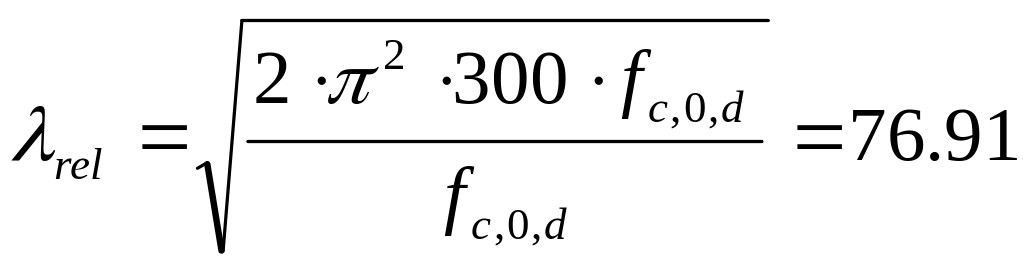k_c= λ²_rel /(2×λ²_z) =76.91²/(2·110,83²)=0,24;

f_c0d = f_c.0.d·k·k_mod·k_h·k_δ/γ_n =1,1×0,8×1,2×0,95×0,94/0,95=0.99 kН/см² =9,9 МПа

где: f_c0d =11 МПа - расчетное сопротивление пихты 3-го сорта сжатию для элементов прямоугольного сечения шириной свыше 0,13 м при высоте сечения от 0,13 до 0,5 м (табл. 6.5 [1]);

к_х=0,8 - переходной коэффициент для пихты, учитывающий по­роду древесины (табл. 6.6 [1]);

k_mod =1,2 - коэффициент условий работы при учёте кратковре­менного действия ветровой нагрузки (табл. 6.4 [1]);

k_h=0,95 - коэффициент, учитывающий высоту сечения, при h > 0,5 м (табл. 6.7 [1]);

k_δ =0,94 - коэффициент, учитывающий толщину слоя, при δ=40 мм (табл. 6.8 [1]).

σ_c.o.d=N_d/A_d=189,93/1280= 0,15 кН/см²;

σ_m.d=M_d/W_d=12,20/13653 =0,001кН/см²;

f_md=f_c.o.d=0.99 кН/см² согласно п. 6.1.4 [1];

k_mc=1- σ_c.o.d /(k_c· f_c.o.d)=1-0,15/(0,24·0.99)=0,37;

, то есть принятое сечение удовлетворяет условиям прочности.

Как видно из расчёта на прочность недонапряжение составляет 85%, но уменьшить высоту сечения невозможно, по условию предельной гибкости.

Проверим принятое сечение на устойчивость плоской формы деформирования по формуле (7.35) [1] (см. п. 6.3.1).

Исходя из предположения, что связи, уменьшающие расчётную дли­ну колонн из плоскости изгиба, ставятся по середине их высот:

l_d.y= μ_о.у·(H_k/2)=1х(930/2)=465см, (5.11)

где μ_о.у=1.0 - при шарнирном закреплении концов стержня из плоскости изгиба (табл. 7.1 [1]);

см;

λ_у=465/5,77=80,59 < λ_mах=120 (табл. 16 [3]);

к_с=76,91²/(2·80,59²)=0,46;

k_inst=140·b²·k_f/(l_d.y·h)=140·0,2²·1,72/(465·0,64)=0,032

где k_f =1,75-0,75хα = 1,75-0,75×0,04 =1,72 принято по табл. 7.4 [1] для трапециидальной формы эпюры моментов при свободной рас­тянутой кромке для нижней половины колонны,

здесь α=1,99/46,40=0,04 при моменте в опорном сечении M_don=46,40 кН·м (см. п. 3.3) и моменте по середине высоты колонны в той же стойке:

M_d,с=((Q_d,w,3+F_x,w,1+F_x,w,2+F_x,w,3)×H+Q_d,w,1×p²/2+Q_d,w,2×((H-p) ×(H+p)/2)×ψ₂ + +F_x,ст×H+M_ст =

=((-9,26-0,13-0,71+9,26)×4,7+1,17×0,5²/2+1.32×[(4,7-0,5)×(4,7+0,5)/2]х0,9+1,96×4,7-16,39) =1,99кНм

Таким образом:

― то есть принятое сечение удовлетворяет условиям прочности.

где: n=2 - показатель степени для элементов без закрепления растянутой зоны из плоскости деформирования. Т.е. устойчивость плоской формы деформирования колонны обеспечена.

Проверим сечение колонны на действие скалывающих напряжений при изгибе по формуле (7.25) [1]:

τ_v.0.d ≤ f_v.0.d,

где τ_v.0.d =V_d·S_sup/(l_sup·b_d),

здесь V_d = V_d /k_m.c=12,2/0,37=32,97 кН - расчётная поперечная сила;

S_sup - статический момент брутто сдвигаемой части попереч­ного сечения колонны относительно нейтральной оси;

l_sup - момент инерции брутто поперечного сечения колонны относительно нейтральной оси;

b_d=b=20,0 см - расчётная ширина сечения колонны;

f_vod = f_v.o.d·k·k_mod ·k_δ/γ_n =1.5·0.8·1.2·0.94/0.95=1.42 МПа,

здесь: f_vod =1.5 МПа - расчетное сопротивление пихты 3-го сорта скалыванию вдоль волокон при изгибе клееных элементов (табл. 6.5 [1]);

к_х=0,8 - переходной коэффициент для пихты, учитывающий породу древесины (табл. 6.6 (1]);

k_mod =1.2 - коэффициент условий работы при учёте кратковре­менного действия ветровой нагрузки (табл. 6.4 [1]);

k_δ =0,94 - коэффициент, учитывающий толщину слоя, при δ=40 мм (табл. 6.8 [1]).

Тогда с учётом того, что для прямоугольных элементов без ослабле­ний

S_sup /l_sup=1.5/h, получаем:

τ_v.0.d = V_d ×S_sup/(I_sup×b_d)=32,97·1.5/(64·20,0)=0,039 кН/см² < f_v.0.d=1,42 кН/см², т.е. условие выполнено.