3.3 Подбор сечения верхнего пояса

Ширину сечения верхнего пояса и элементов решётки принимаем одинаковой. Подберём её из условим предельной гибкости λ_max =150 для самого длинного раскоса е-ж , у которого

l_z =l_y= 3,756м.

b = l_y/(0,289×λ_max) = 3,756/(0,289×150) =0,087м

Исходя из условия обеспеченности опирания конструкции покрытия, принимаем верхний пояс сечением b×h=11,5×24 см.

Геометрические характеристики сечения пояса:

,

,

Расчётная длина элемента :

l_d,z = μ₀×l_z =1×3,756 =3,756 м

μ₀ =1 – при шарнирно закреплённых концах стержня.

Радиус инерции сечения в направлении соответствующей оси:

λ_z = l_d,z/i_z=3,756×100/6,93= 54,2< λ_max =120

λ_rel =

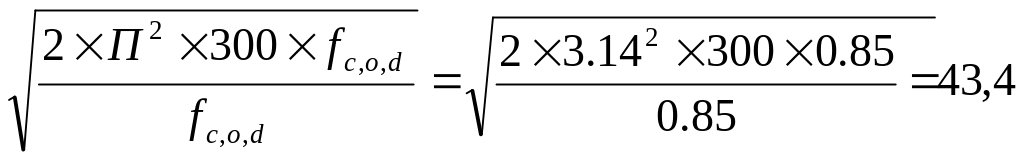
k_c =λ²_rel /(2×λ²_z) =43,4² /(2×54,2²) =0,32

k_c –коэффициент продольного изгиба

k_m,c = 1-(G_c,o,d/(k_c×f_c,o,d)) = 1-(0,024/(0,32×0,826)) = 0,909

k_m,c – коэффициент учитывающий увеличение напряжения при изгибе от действия продольной силы.

f_c,o,d = f_c,0,d×к_х×k_mod,1×k_h×k_δ/γ_n=0,85×0,8×1,05×1×1,1/0,95=0,826 кН/cм²

f_c,0,d =0,85 – расчётное сопротивление пихты сжатию, 3-го сорта, вариант а. табл. 6.5 СнБ

k_mod=1,05 – коэффициент условий работы, 3 класс отв-ти,.

k_h – коэффициент, учитывающий высоту сечения.

k_δ=1.1 – коэффициент, учитывающий толщину слоя, при б<19.

N_d = (G_d+Q_d)×l_d/2= (0,794+0,616)×3,756/2=2,65 кН

N_d – продольная сила.

G_c,o,d = N_d/A_d=2,65/276 =0,01 кН/cм²

G_c,o,d – расчётное напряжения древесины сжатия.

М_d = F_d×l²/8 = (0,794+0,616)× 3,756²/8 = 2,49 кНм

W_d=b×h²/6 =11,5×24²/6 = 1104 см³

G_m,d= М_d/W_d= 2,49 /1104×100=0,23 кН/cм²

G_m,d – расчётное напряжение изгиба.

Проверим сечение сжато изогнутого элемента.

(G_c,o,d/f_c,o,d)+(G_m,d/k_m,c /f_m,d ) ≤1; (0,01/0,826)+( 0,23/0,909/0,85)=0,31<1

Исходя из предположения, что связи будут раскреплять панели пояса фермы по концам и в середине:

l_d,y =μ₀×l_z ×0,5=1×375.6×0,5=187.8 м

i_y=

λ_y =l_d,y/i_y =187.8/6,93 =27,01< λ_max =120

k_c = λ²_rel /(2×λ²_y) = 43,4 /(2×27,01²) =0,03

k_m,c = 1-(G_c,o,d/(k_c×f_c,o,d)) = 1-(0,01/(0,03×0,826)) =0,725

k_inst = 140×b²×k_f/(l_m×h) =140×0.115²×1,75/(1,878×0.24) =7.189

k_f – коэффициент зависящий от формы эпюры огибающих моментов.

Проверим принятое сечение на устойчивость плоской фермы деформирования.

(G_c,o,d/f_c,o,d/k_с)+(G_m,d/k_m,c /f_m,d/k_inst)² =(0,01/0,725/0,03)+(0,23/0,725 /0,826/7,189)² =0,26<1

Т.е. устойчивость плоской формы деформирования панелей верхнего пояса фермы обеспечена.

3.4 Расчет раскосов

Все раскосы проектируем одинакового сечения. За расчётное усилие ,принимаем усилие по таблице 4.1. Расчёт ведём для самого длинного раскоса е-ж.

Исходя из предельной гибкости h= l_z/(0,289×λ_max) = 3,756/(0,289×150) =0,087 м.

Принимаем сечение раскосов b×h=19×11,5см

A_d = h×b=19×11.5=218,5 см² >50 см²

I_y,sup= h×b³/12 = 19×11.5³/12 =2408,05 см⁴

l_d,y= μ₀×l_z = 1×3,756 =3,756м

i_y=

λ_y =l_d,y/i_y =3,756×100/3,32=113,13< λ_max=150

k_c = λ²_rel /(2×λ²_y) = 43,4² /(2×113,13²) =0,07

N_d = (G_d+Q_d)×l_d/2= (0,794+0,616)×3,756/2=2,65 кН

G_c,o,d = N_d/A_d= 2,65/218,5=0,012 кН/cм² <k_c ×f_c,o,d = 0,07 ×0,826 =0,06 кН/cм²

f_c,o,d = f_c,0,d×к_х×k_mod,1×k_h×k_δ/γ_n=0,85×0,8×1,05×1×1,1/0,95=0,826 кН/cм²