Задание 2

2.1.Метод трапеций вычисления интеграла

Рассмотрим вычисления определенного интеграла

Этот интеграл приближенно заменяем площадью заштрихованной трапецией, ограниченной сверху прямой линией, проходящей через точки (0, f0) и (h, f1). Функция и трапеция показана на Рис.2.1.

Рис.2.1. К расчету интеграла по формуле трапеций

Указанная прямая задается уравнением

в чем нетрудно убедиться, положив поочередно x равным 0 и h.

Отсюда находим, интегрируя у(х)

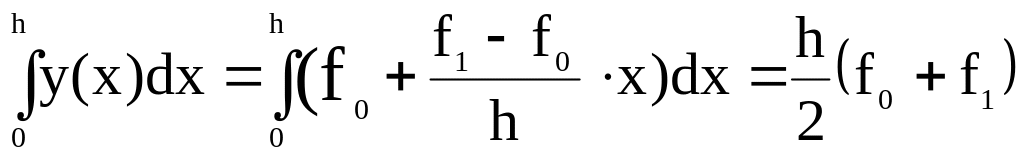
Таким образом, формула трапеций имеет вид

)

Однако на большом интервале формула (2.1) имеет значительную погрешность. Выведем усложненную формулу для приближенного вычисления интеграла на произвольном отрезке [a, b]

Разобьем отрезок интегрирования [a, b] на n элементарных частей. Длина каждой части

Тогда границы элементарных отрезков xj =a + j*h, а значения функции в этих точках fj = f(xj), где j = 0, 1, …, n.

Перепишем каноническую квадратурную формулу трапеций (2.1.) применительно к отрезку [xi, xi+1] длины h

Суммируя левую и правую части этого соотношения от i=0 до i=n-1, получаем усложненную (обобщенную) квадратурную формулу трапеций.

По этой формуле будем производить вычисления для заданной функции.

2.2.Постановка задачи вычисления интеграла

Для вычисления интеграла по формуле (2.2) необходимо:

ввести начало и конец интервала интегрирования;

ввести число разбиений интервала интегрирования;

вычислить длину элементарного отрезка;

вычислить значение интеграла по формуле (2.2).

Вычисление значения подинтегральной функции целесообразно организовать в отдельной программе.

Составим таблицу идентификаторов, применяемых в программе:

Идентификатор	Описание
a	Начало интервала
b	Конец интервала
n	Число разбиений
h	Длина элементарного отрезка
Sum	Значение суммы по формуле (2.2)
integ	Значение интеграла

Текст программы на языке Pascal, составленный по описанному алгоритму, приводится в Приложении 2.

2.3.Результаты расчета значения интеграла

Окно программы после выполнения расчета показано на рис.2.2.

Рис. 2.2. Окно программы вычисления интеграла

Для проверки правильности решения можем использовать систему MathCAD.

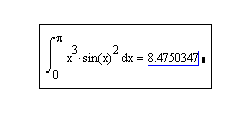
Заключение

В данной курсовой работе рассмотрена задача решения уравнения численным методом и задача вычисления определенного интеграла с помощью компьютера.

Результаты исследования показывают, что применение численных методов должно осуществляться на строго определенных математических понятиях. Так, например, в рассмотренном методе хорд неправильный выбор начального приближения корня приведет к расходимости итерационного процесса и невозможно­сти решения поставленной задачи решения уравнения.

Выбор алгоритма для вычислений – весьма важный момент при практиче­ском решении задачи. Здесь немалую роль играют такие свойства алгоритма, как простота, надежность, экономичность и т. д. Одной из характеристик вычислительного алгоритма является его скорость сходимости.

Приведенные результаты расчета показывают, что уточнение корня уравне­ния методом хорд дает результат с очень высокой точностью даже при нескольких итерациях расчета. Метод хорд не использует значение производной функции, что позволяет при одинаковом объеме вычислений сделать вдвое больше итераций и за счет этого получить вдвое большую точность.

В численном интегрировании методом Симпсона необходимо обосновать выбор числа элементарных отрезков интегрирования для достижения заданной точности расчета.