Ярошевич Владислав Андреевич

Задание на курсовую работу

Задание 1

Найти корни уравнения

на интервале [-1,0] методом итераций с точностью 0.001.

Задание 2

Найти значение интеграла

методом трапеций с точностью 0.01.

Оглавление

Введение 2

Задание 1 5

1.1.метод касательных решения нелинейных уравнений. 5

1.2.постановка задачи решения уравнения 7

1.3.результаты расчета корней уравнения 9

Задание 2 11

2.1.метод трапеций вычисления интеграла 11

2.2.постановка задачи вычисления интеграла 13

2.3.результаты расчета значения интеграла 14

Заключение 15

Список литературы 16

Приложение 1 17

Приложение 2 19

Введение

Очень часто на практике в большинстве случаев найти точное решение возникшей прикладной задачи не удается. Это происходит главным образом потому, что искомое решение обычно не выражается в привычных элементарных или других известных функциях.

Например, общих аналитических приемов решения трансцендентных уравнений не существует. Трансцендентное — это уравнение, не являющееся алгебраическим. В алгебре доказано, что не существует также теоретического решения алгебраических уравнений пятого и более высокого порядка. Поэтому на практике обычно пользуются приближенными методами нахождения корней.

Вторым примером является задача численного интегрирования. На практике в редких случаях удается вычислить точно определенный интеграл, ряд интегра­лов не выражаются в элементарных функциях.

Для решения такого рода задач применяются численные методы. Под численными методами подразумеваются методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, т. е. к тем действиям, которые выполняет электронная вычислительная машина. В зависимости от сложности задачи, заданной точности, применяемого метода и т. д, может потребоваться выполнить от нескольких десятков до многих миллиардов действий.

Особо важное значение приобрели численные методы в связи с возрастанием роли математических методов в различных областях науки и техники и с появлением высокопроизводительных электронных вычислительных машин. К последним в полной мере можно отнести и современные персональные компьюте­ры, которые находятся в широком использовании и в состоянии решать многие научные и инженерные задачи высокой сложности.

Решение, полученное численным методом, обычно является приближенным, т. е. содержит некоторую погрешность. Источниками погрешности приближенного решения являются:

несоответствие математической модели изучаемому реальному явлению;

погрешность исходных данных;

погрешность метода решения;

ошибки округления в арифметических и других действиях над числами. Однако приближенное решение, полученное с высокой степенью точности

можно считать эквивалентным точному решению.

Данная курсовая работа ставит своей целью обучение процессу анализа, изучения и численного решения прикладных задач с использованием компьютера.

Для численного решения прикладных задач в ходе выполнения курсовой работы необходимо освоить математические методы численного решения, а также средства и технологии программирования на языке Паскаль.

Задание 1

1.1.Метод касательных решения нелинейных уравнений.

Метод касательных, называемый также методом Ньютона, состоит в следующем. Рассмотрим в точке х0 касательную к кривой у=f(x). Уравнение касательной имеет вид

y = f(x0) + (x - x0)f’(x0)

Положив у=0, находим точку х1 пересечения касательной с осью абсцисс

Построив касательную к точке х1 (Рис.1.1), получаем по аналогичной формуле точку х2 пересечения этой касательной с осью х. Продолжая аналогичным образом, приходим к общей формуле

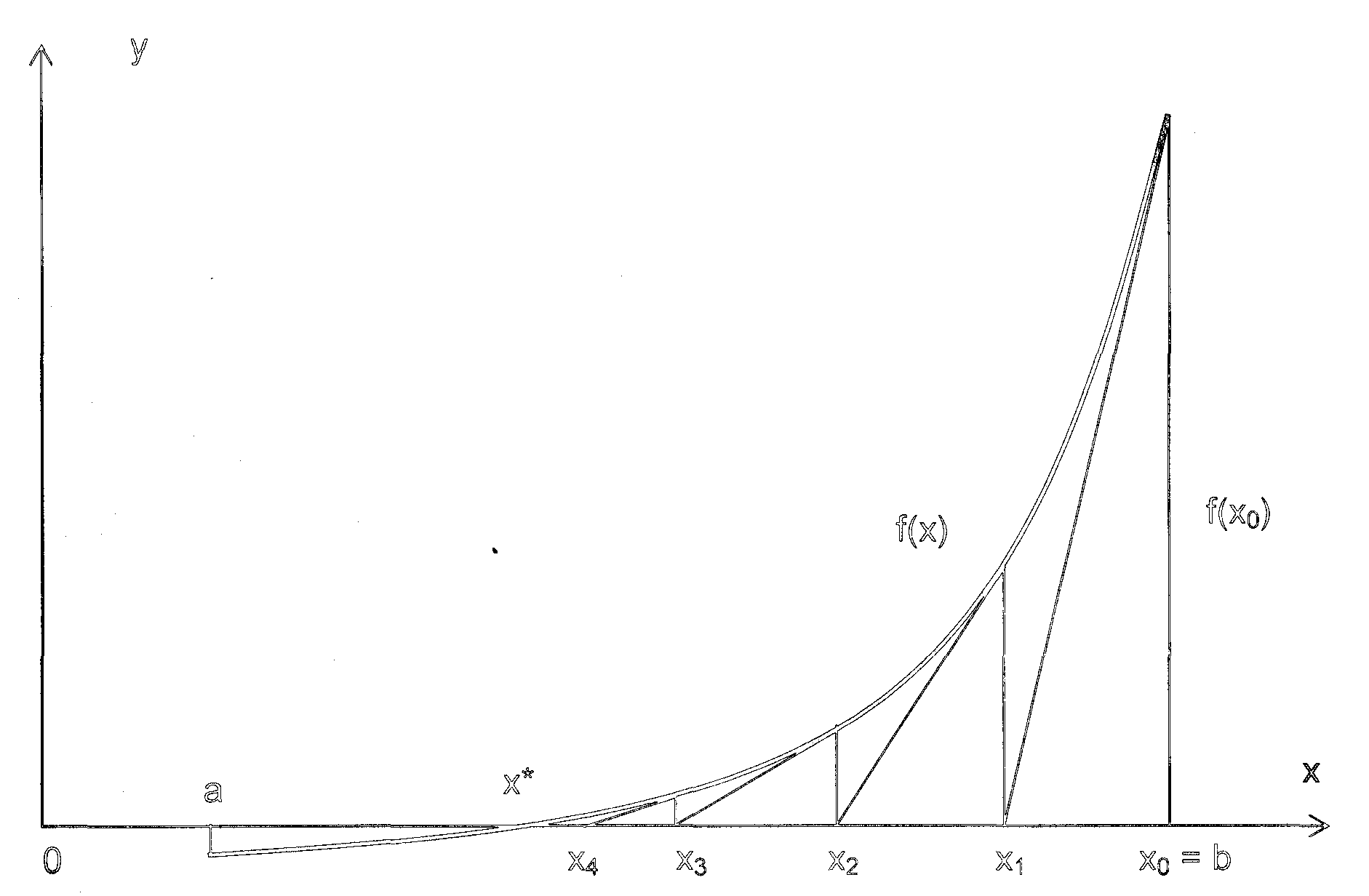
Рис.1.1. Геометрический смысл метода касательных.

Процесс получения точек данной последовательности показан на Рис.1.1. Начальное приближение х0 = а или х0 = b можно выбирать таким образом, чтобы вся последовательность приближений х1, х2, …, хk, … принадлежала интервалу [a, b]. В случае существования производных f’, f’’, сохраняющих свои знаки на интервале [a, b] за х0 берется тот конец отрезка [a, b] для которого выполняется условие

f(x0) f’’(x0) > 0 (1.2)

Сходимость метода касательных к точному решению х* определяется следующей теоремой.

Теорема. Пусть на отрезке [a, b] отделен корень с уравнением f(x) = 0. Если на [a, b] производные f’, f’’ отличны от нуля и сохраняют определенные знаки, то метод касательных сходится.