Основные термические параметры состояния

Понятие термических параметров состояния относится к таким параметрам, которые могут быть непосредственно измерены с помощью приборов. К основным термическим параметрам состояния относятся: удельный объем, давление и температура.

Удельный объем

Удельный объем – это объем единицы массы вещества (м³/кг):

, (1.1)

где V – объем тела, м³; m – масса тела, кг.

Величина, обратная удельному объему, называется плотностью (кг/м³):

. (1.2)

В практике часто используется понятие удельного веса – это вес единицы объема тела (Н/м³):

, (1.3)

где g – ускорение свободного падения (приблизительно 9,81 м/с²).

При переводе любой величины в СИ, например  из 1 г/см³, необходимо руководствоваться следующим правилом: все величины формулы (1.3) представляют в единицах СИ и выполняют с ними действия арифметическими операторами формулы:

 = 1 г/см³ = 9,81·10^-3/10^-6 = 9,81·10³ Н/м³.

При этом надо помнить, что 1 кгс = 9,81 Н. Этим соотношением часто пользуются при переводе несистемных единиц в СИ.

Давление

Давление – это силовое воздействие (F) тела и его частей на окружающую среду или оболочку и на соседние части того же тела на единицу поверхности (S). Это силовое воздействие направлено перпендикулярно к любому элементу поверхности и уравновешивается обратно направленным силовым воздействием окружающей среды, оболочки или соседнего элемента того же тела.

.

В СИ используется единица давления паскаль (Па), это 1 Н/м², т.е. сила в один ньютон, действующая по нормали на площадь в один квадратный метр. Для технических измерений паскаль очень небольшая величина, поэтому ввели кратную паскалю единицу давления бар: 1 бар = 10⁵ Па. Выбор этой единицы измерения давления объясняется тем, что атмосферное давление воздуха над поверхностью Земли приблизительно равно одному бару.

В технике часто используется единица давления в старой системе измерения (СГС) – техническая атмосфера: 1 атм = 1 кгс/см² (не путать с понятием физической атмосферы).

Часто измеряют давление, особенно небольшое, высотой столба жидкости (ртуть, вода, спирт и т.д.). Столб жидкости (рис.1.5) производит на основание сосуда давление, определяемое равенством

Р = F/S = HSρg/S = ρgH, (1.4)

где ρ – плотность жидкости, кг/м³;

Н – высота столба жидкости, м;

g – ускорение свободного падения, м/с²;

F, S – сила, действующая на дно сосуда, и его площадь.

Из уравнения (1.4) следует, что давлению Р соответствует высота столба жидкости Н = Р/(ρg), т.е. высота Н прямо пропорциональна давлению, поскольку ρg – величина постоянная.

В практике высоту столба жидкости часто берут для оценки давления. Поэтому метры и миллиметры столба жидкости стали единицами измерения давления. Для перехода от высоты столба жидкости к паскалям необходимо в формулу (1.4) подставить все величины в СИ.

Н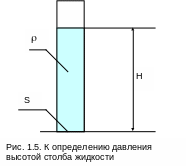 апример, при 0 ^оC плотность воды составляет 1000 кг/м³, ртути – 13595 кг/м³ в земных условиях. Подставив эти величины в формулу (1.4), получим соотношения для 1мм столба этих жидкостей и давления в паскалях:

Н = 1 мм вод.ст. соответствует Р= 10³·9,81·10^-3= 9,81 Па;

Н = 1 мм рт.ст. соответствует Р = 13595·9,81·10^-3= 133,37 Па.

При определении давления высотой столба жидкости необходимо учитывать изменение ее плотности в зависимости от температуры. Это необходимо делать для сопоставления результатов измерения давления. Так, при определении атмосферного давления с помощью ртутного барометра его показания приводятся к 0 ^оС исходя из соотношения

В_о = В (1 - 0,000172 t), (1.5)

где В – действительная высота ртутного столба барометра при температуре ртути t ^оС;

В_о – показания барометра, приведенные к температуре 0 ^оС.

В расчетах используются давления столбов жидкости, приведенные к температуре 0 ^оС.

Измерение давления в технике основано на показаниях различных приборов, действующих по принципу отражения на шкале величины, численно равной разности давлений в месте замера и давления окружающей среды. Как правило, приборы имеют положительную шкалу, т.е. разность между большим и меньшим давлением. Поэтому они подразделяются на приборы для замера давления: больше атмосферного – манометры, меньше атмосферного – вакуумметры.

П ример таких приборов в виде жидкостных U-образных манометров (вакуумметров) показан на рис. 1.6.

Давление по шкале этих приборов называется манометрическим давлением Р_М и вакуумом Р_В соответственно. Давление в месте замера называется абсолютным Р, окружающей среды – давлением атмосферного воздуха или барометрическим В, поскольку прибор, как правило, установлен в окружающем его атмосферном воздухе.

Расчетные зависимости давления по приборам будут следующие:

манометрическое давление:

Р_М = Р - В, (1.6)

где Р_М – манометрическое давление (по прибору);

Р – абсолютное давление;

В – давление атмосферного воздуха (барометрическое давление);

вакуум:

Р_В = В - Р, (1.7)

где Р_В – вакуум (показания вакуумметра).

Параметром состояния термодинамического тела является абсолютное давление, при использовании приборов оно будет определяться в зависимости от типа прибора по следующим зависимостям:

для манометра

Р = Р_М + В, (1.8)

для вакуумметра

Р = В - Р_В . (1.9)