3.1.2. Теплоемкости газов

Понятие теплоемкости рассмотрено в разд. 2.2. Применим это понятие для газов, систематизируя разновидности теплоемкостей.

Удельные теплоемкости

Удельная массовая теплоемкость – это количество теплоты, необходимое для нагрева 1 кг газа на один градус. Она обозначается буквой с, имеет единицу измерения Дж/(кгград), определяется как

c = Q/(mdt) = q/dt . (3.17)

Удельная мольная теплоемкость – это количество теплоты, необходимое для нагрева одного моля (киломоля) газа на один градус. Ее обозначение с_, единица измерения Дж/(кмольград), расчетное выражение соответствует произведению молярной массы газа на его удельную массовую теплоемкость, т.к. в одном киломоле содержиться  килограммов газа:

с_ = с , (3.18)

где  – молекулярная масса газа, кг/кмоль.

Удельная объемная теплоемкость газа – это количество теплоты, необходимое для нагрева одного кубического метра газа на один градус. Ее обозначение с', единица измерения Дж/(м³град), расчетное выражение соответствует следующим соотношениям:

c' = Q/(Vdt) = C /V = mQ/(mVdt) =

= m/V(q/dt) = c = c/v = c_/V_ , (3.19)

где  – плотность газа, кг/м³;

v – удельный объем газа, м³/кг;

V_ – объем 1 киломоля газа, м³/кмоль.

Плотность газа и объем одного киломоля газа зависят от температуры и давления, поэтому при различных параметрах объемная теплоемкость одного и того же газа различна даже в случае постоянной ее удельной массовой теплоемкости. Для практического пользования такой теплоемкостью необходимо к каждому ее значению указывать соответствующие ему значения температуры и давления газа, что очень неудобно. В справочной литературе принято давать объемную теплоемкость газа, отнесенную к одному кубическому метру газа, взятому при нормальных физических условиях – 0 ^оС и 760 мм рт.ст. (нм³). При нормальных условиях один киломоль любого идеального газа занимает объем 22,4 м³. При этих условиях удельную объемную теплоемкость идеального газа удобно определять как

с' = с_/22,4 , (3.20)

в единице измерения этой теплоемкости присутствует нормальный кубический метр газа, Дж/(нм³град).

Теплоемкости процессов

Поскольку теплота является функцией процесса, то и теплоемкость есть функция процесса. На практике наибольшее применение нашли теплоемкости изобарного – c_p при Р=const и изохорного – c_v при v=const процессов.

Теплоемкости идеальных газов

Воспользуемся первым законом термодинамики для получения аналитических выражений изохорной и изобарной теплоемкостей идеальных газов:

c = q/dT = du/dT + /dT = du/dT + Pdv/dT . (3.21)

При v=const (dv=0) из выражения (3.21) получим аналитическое выражение для изохорной теплоемкости:

с_v = (du/dT)_v . (3.22)

Подставив с_v в выражение дифференциала внутренней энергии при независимых переменных T и v, получим выражение

du = (du/dT)_vdT + (du/dv)_Tdv = c_vdT + (du/dv)_Tdv . (3.23)

Для идеального газа внутренняя энергия – функция только одного термического параметра – температуры, т.е. (du/dv)_T=0. Следовательно, для идеального газа выражение (3.23) примет вид

du = c_vdT . (3.24)

Аналитическое выражение изохорной теплоемкости идеального газа получается из (3.24) и выражения внутренней энергии идеального газа:

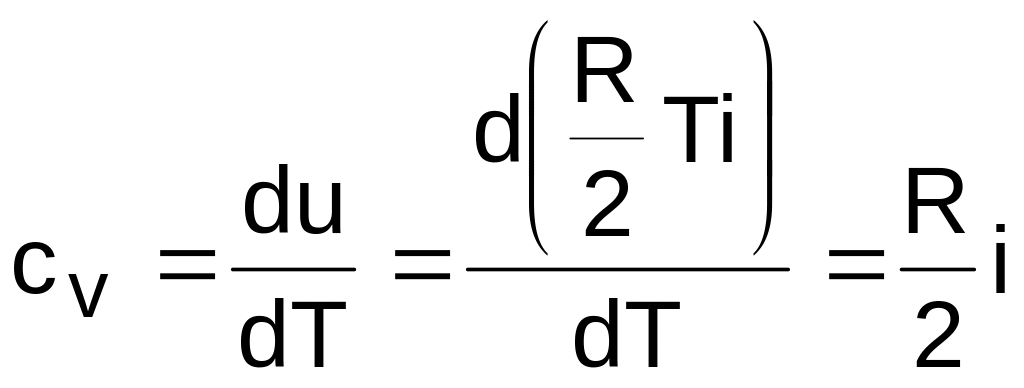. (3.25)

Из выражения (3.25) следует, что изохорная теплоемкость идеального газа величина постоянная.

Подставив выражение изохорной теплоемкости идеальных газов (3.25) в уравнение (3.21), получим выражение теплоемкости идеального газа в виде

c = c_v + Pdv/dT . (3.26)

Рассмотрим выражение (3.26) применительно к идеальному газу для изобарного процесса P=const. Второе слагаемое выражения (3.26) для идеального газа при P=const можно получить дифференцированием уравнения Менделеева – Клапейрона:

Pv=RT , при Р=const Pdv=RdT  Pdv/dT=R .

В результате этих преобразований получаем расчетное выражение для изобарной теплоемкости идеального газа:

c_p = c_v + R . (3.27)

Уравнение (3.27) носит название формула Майера. Используя формулу Майера, получим аналитическое выражение изобарной теплоемкости идеального газа:

. (3.28)

Изобарная теплоемкость идеального газа больше изохорной теплоемкости на величину газовой постоянной.

Аналитические выражения для удельных мольных и объемных изохорных и изобарных теплоемкостей идеального газа легко получить, используя их взаимосвязь с удельными массовыми теплоемкостями (3.25) и (3.28):

Дж/(кмольК); (3.29)

Дж/(кмольК); (3.30)

, Дж/(нм³К); (3.31)

Дж/(нм³К). (3.32)

В соответствии с молекулярно-кинетической теорией идеальных газов их изобарные и изохорные теплоемкости (выражения (3.25), (3.28) – (3.32)) – величины постоянные, не зависящие от термических параметров состояния газа.

В системе единиц, основанной на калории (1ккал=4187кДж) мольная теплоемкость идеального газа определяется простым соотношением (ккал/(кмольК)):

c_v  i ; (3.33)

c_p  (i+2) . (3.34)