Примеры

Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:

1) ;

2) ;

3) ;

4) .

Решение: 1) Члены данного ряда по абсолютной величине монотонно убывают: и . Следовательно, согласно признаку Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.

Ряд , составленный из абсолютных величин членов данного ряда, который, как, известно, расходится. Поэтому данный ряд сходится условно.

2) Члены данного ряда по абсолютной величине монотонно убывают , но 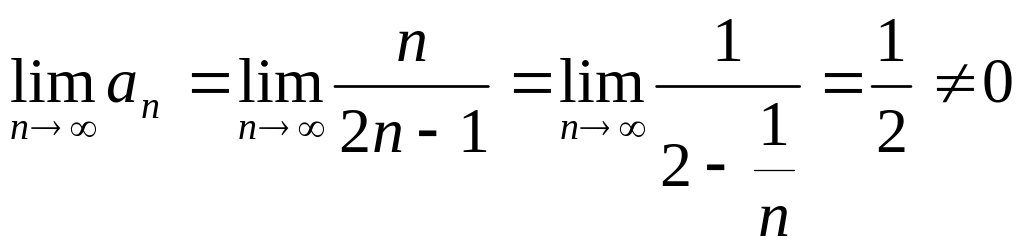. Ряд расходится, так как признак Лейбница не выполняется.

3) Используя признак Лейбница, получим ; , то есть ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: . Это геометрический ряд вида , который сходится. Поэтому данный ряд сходится абсолютно.

4) Используя признак Лейбница, имеем ; , то есть ряд сходится.

Рассмотрим ряд, составленный из абсолютных величин членов данного рада: , или . Это обобщенный гармонический ряд, который расходится, так как . Следовательно, данный ряд сходится условно.

Задания для практической работы

1. Используя признак Лейбница, исследуйте сходимость знакочередующегося ряда:

1) ;

2) ;

3) ;

4) .

2. Исследуйте на сходимость (абсолютную или условную) знакочередующиеся ряды:

1) ;

2) ;

3) ;

4) ;

5) .

Вопросы для самоконтроля:

1. Какой ряд называется знакопеременным?

2. Какой ряд называется знакочередующимся?

3. Сформулируйте признак Лейбница для знакочередующихся рядов.

4. Какой ряд называется абсолютно сходящимся, условно сходящимся?

5. Какие признаки используются для установления абсолютной сходимости знакопеременного ряда?

Рекомендуемая литература: 1.2, 1.3, 1.4, 1.5, 2.2, 2.3, 2.4, 2.5

Практическая работа №24

Тема: Действия над комплексными числами в тригонометрической и показательной формах

Цель: Формирование навыков выполнения действий над комплексными числами в тригонометрической и показательной формах

Время выполнения: 2 часа

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Комплексными числами называются числа вида , где и - действительные числа, а число , определяемое равенством , называется мнимой единицей.

Запись комплексного числа в виде называется алгебраической формой записи комплексного числа.

Представление комплексного числа в виде , где , называется тригонометрической формой записи комплексного числа.

Произведение комплексных чисел и находится по формуле:

то есть

, .

Таким образом, при умножении двух комплексных числе, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.

Частное комплексных чисел и находится по формуле:

,

то есть

, .

Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, аргументы вычитаются.

При возведении комплексного числа в -ую степень используется формула

,

которая называется формулой Муавра.

Для извлечения корня -ой степени из комплексного числа используется формула

,

где - арифметический корень, .

Степень с комплексным показателем определяется равенством

.

Можно доказать, что

,

то есть

. (24.1)

В частности, при получается соотношение

,

которое называется формулой Эйлера.

Для комплексных показателей остаются в силе основные правила действий с показателями; например, при умножении чисел показатели складываются, при делении – вычитаются, при возведении в степень – перемножаются.

Показательная функция имеет период, равный , то есть . В частности, при получается соотношение .

Тригонометрическую форму комплексного числа можно заменить показательной формой: .

Умножение, деление, возведение в целую положительную степень и извлечение корня целой положительной степени для комплексных чисел, заданных в показательной форме, выполняются по следующим формулам:

;

;

;

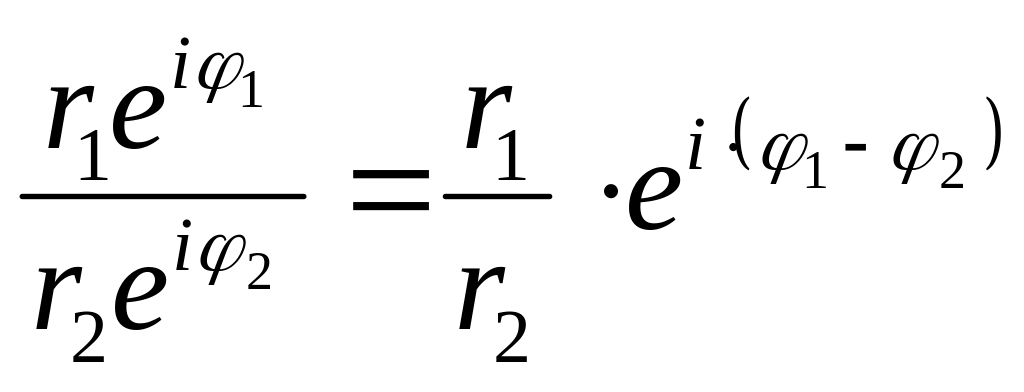, где .