Практическая работа №7 Тема: Составление уравнений кривых второго порядка, их построение
Цель: Формирование навыков составления уравнений кривых второго порядка, их построения
Время выполнения: 2 часа.
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Окружностью называется множество точек плоскости, равноудаленных от данной точки этой плоскости, называемой центром.
Уравнение окружности
с центром в начале координат и радиусом
имеет вид
.
Уравнение окружности
с центром в точке
и радиусом
имеет вид
.
Уравнение окружности
в общем виде записывается так:
,
где
,
,
и
- постоянные коэффициенты.
Эллипсом
называется множество точек плоскости,
сумма расстояний которых до двух данных
точек, называемых фокусами, есть величина
постоянная
,
большая расстояния между фокусами
.
Уравнение эллипса,
фокусы которого лежат на оси
,
имеет вид
,
где
- длина большей полуоси;
- длина малой полуоси.
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная , меньшая расстояния между фокусами .
Уравнение гиперболы,
фокусы которого лежат на оси
,
имеет вид
,
где
- длина действительной полуоси;
- длина мнимой полуоси.
Параболой называется множество точек на плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.
Уравнение параболы
с вершиной в начале координат, осью
симметрии которой служит ось
и ветви направлены вверх, имеет вид
,
где
(параметр параболы) – расстояние от
фокуса до директрисы. Уравнение ее
директрисы
.
Задания для практической работы
Составьте уравнение окружности с центром в точке
и радиусом, равным 3.Составьте уравнение окружности, проходящей через точк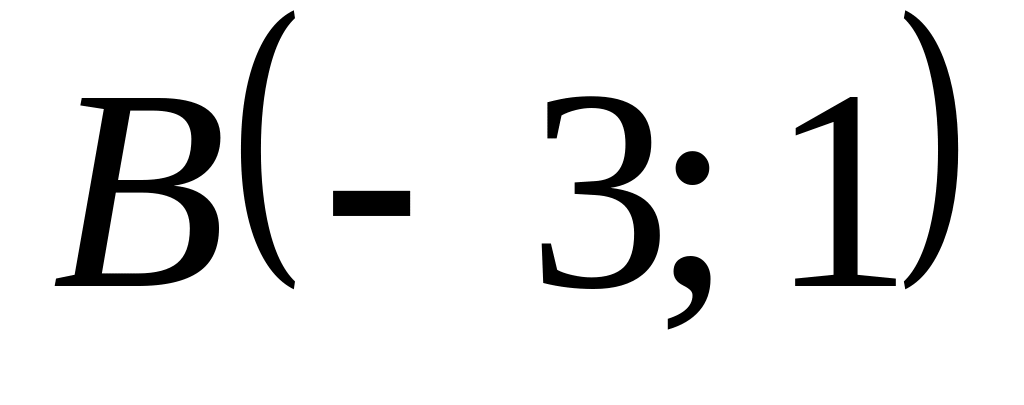и
,
и
.
Изобразите полученную окружность в
прямоугольной системе координат.Составьте уравнение окружности, проходящей через точк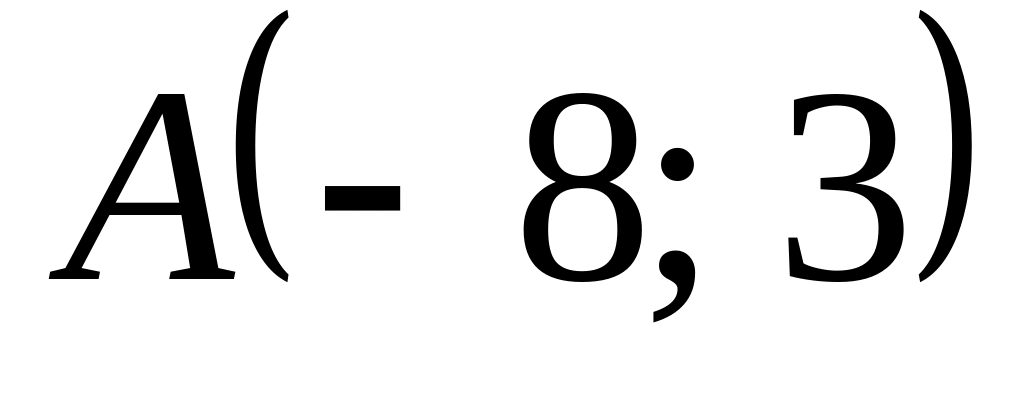и
и
,
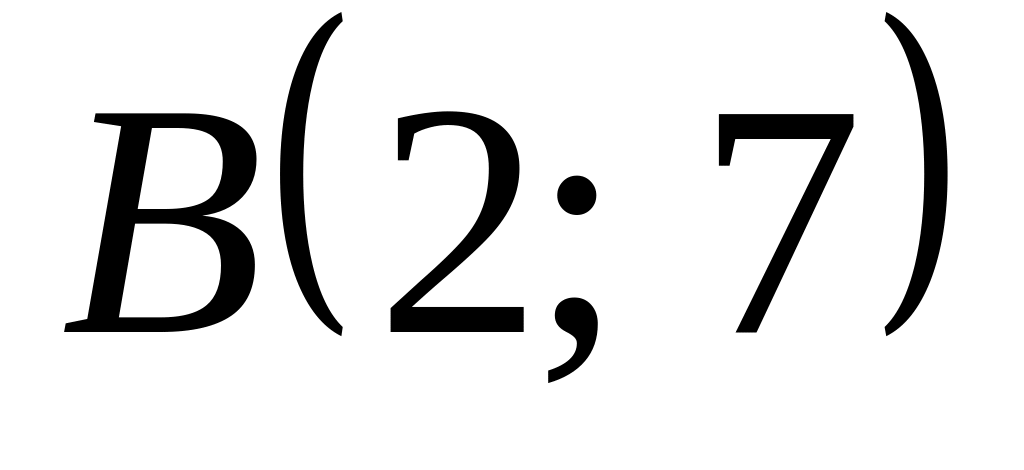если ее центр лежит на прямой
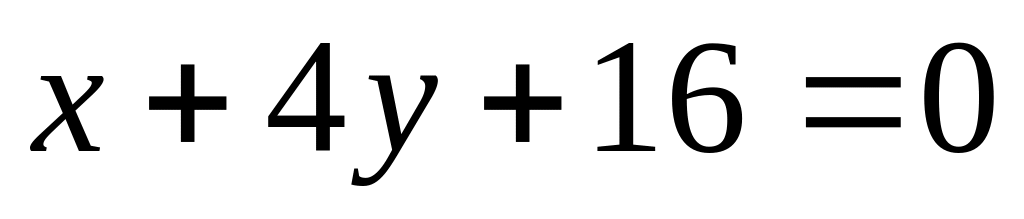.Составьте уравнение эллипса с фокусами на оси , если большая ось равна 10, а эксцентриситет
.
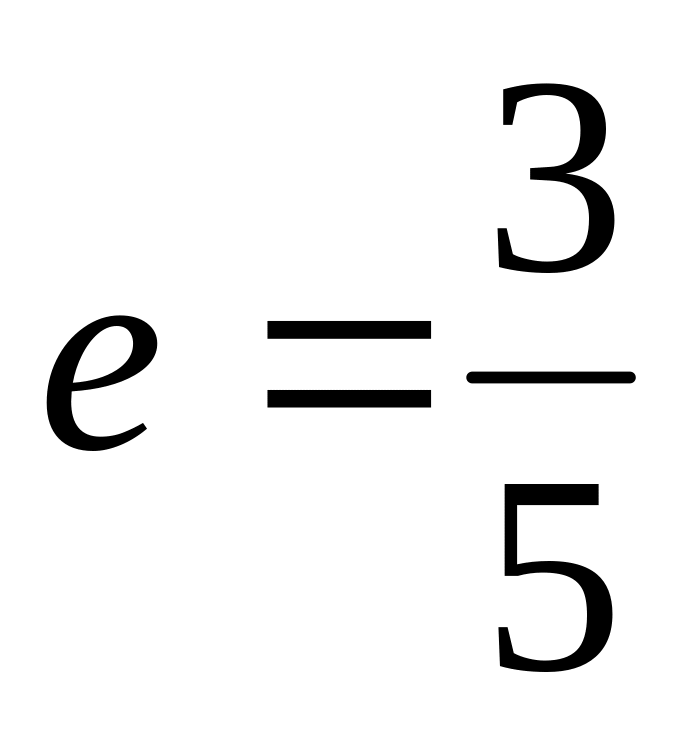Изобразите найденный эллипс в
прямоугольной системе координат.Составьте уравнение эллипса с фокусами на оси , если он проходит через точк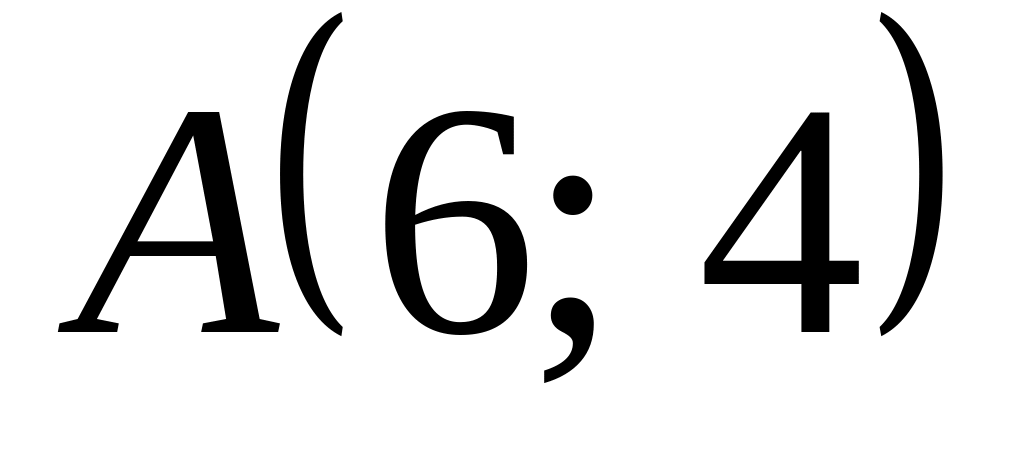и,
и
.
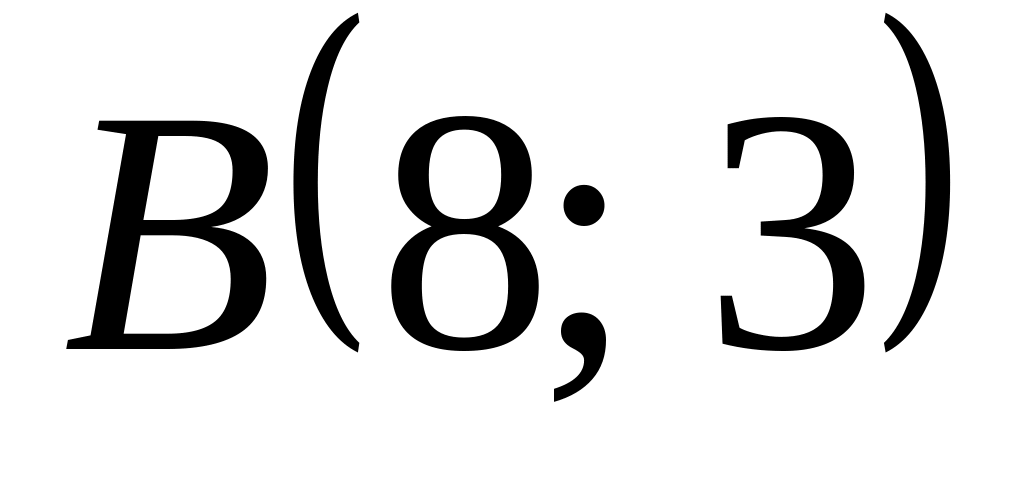Постройте полученный эллипс в
прямоугольной системе координат.Дано уравнение гиперболы
.
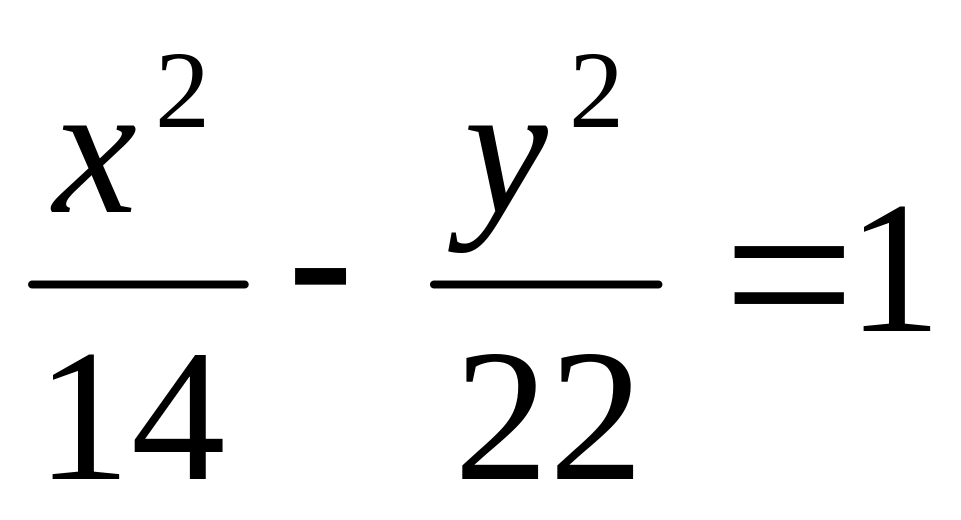Найдите координаты фокусов и расстояние
между ними.Составьте уравнение гиперболы с фокусами на оси , если длина ее действительной оси равна 6, а эксцентриситет равен
.
Постройте найденную гиперболу в
прямоугольной системе координат.Найдите точки пересечения параболы
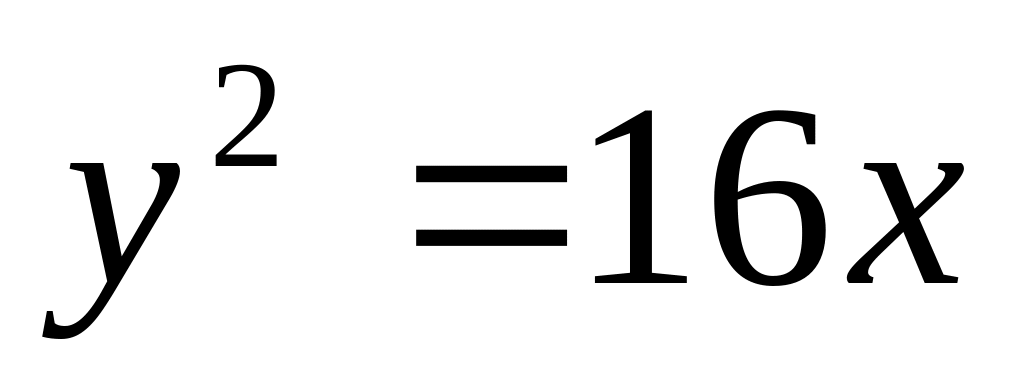с прямой
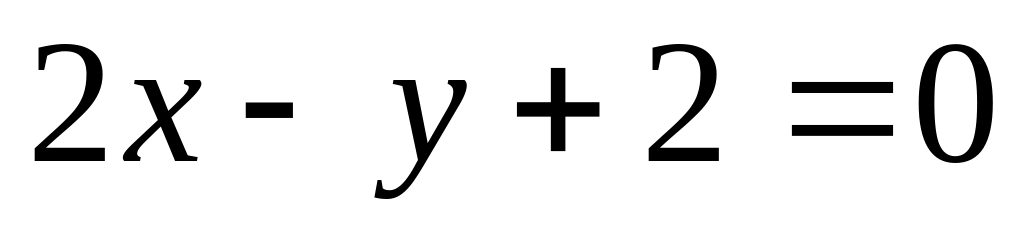.Составьте уравнение оси параболы
.Составьте уравнение директрисы параболы
.
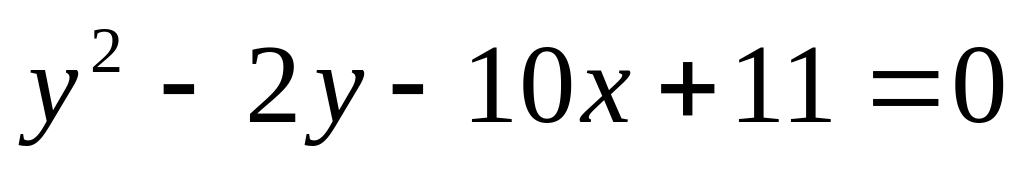Вопросы для самоконтроля:
Что называется окружностью?
Какой вид имеет уравнение окружности с центром в начале координат, с центром в произвольной точке?
Что называется эллипсом?
Какой вид имеет уравнение эллипса с фокусами на оси , на оси ?
Что называется эксцентриситетом эллипса? По какой формуле он вычисляется?
При помощи какого соотношения выражается зависимость между параметрами эллипса?
Что называется гиперболой?
Какой вид имеет уравнение гиперболы с фокусами на оси ?
При помощи какого соотношения выражается зависимость между параметрами гиперболы?
Какая гипербола называется равносторонней? Запишите ее уравнение.
Что называется параболой?
Какой вид имеет уравнение параболы с вершиной в начале координат?
Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.1, 2.3, 2.4, 2.5