Задание для практической работы

Пользуясь методом исключения неизвестных, найдите общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное. Для частного и базисного решений необходимо сделать проверку.

.

Вопросы для самоконтроля:

1. Дайте определение эквивалентных (равносильных) систем линейных алгебраических уравнений.

2. Назовите элементарные преобразования, не нарушающие равносильности систем линейных алгебраических уравнений.

3. В чем состоит сущность метода Жордана – Гаусса для решения систем линейных алгебраических уравнений? Как осуществляется этот метод? Когда он применим?

4. Что называется общим решение системы линейных алгебраических уравнений?

5. Какие переменные называются базисными, а какие свободными?

6. Как найти частное решение систем линейных алгебраических уравнений? Сколько частных решений имеет система линейных алгебраических уравнений?

7. Что называется базисным решением системы линейных алгебраических уравнений? Сколько базисных решений имеет система линейных алгебраических уравнений?

Рекомендуемая литература: 1.2, 1.3, 1.4, 2.1, 2.3, 2.5

Практическая работа №5 Тема: Действия над векторами. Вычисление модуля и скалярного произведения

Цель: Формирование навыков выполнения операций над векторами и вычисления модуля и скалярного произведения векторов.

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Отрезок называется направленным, если один из его концов считается началом отрезка, а другой – его концом.

Вектором называется направленный отрезок. Вектор, заданной парой несовпадающих точек, обозначается символом . Точка называется началом, а точка - концом вектора.

Расстояние | | называется диной (модулем) вектора .

Вектор , концы которого совпадают, называется нулевым вектором. Длина нулевого вектора равна нулю.

Два вектора называются коллинеарными, если они лежат на одной или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.

Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними: .

Скалярное произведение векторов и выражается через их координаты по формуле .

Угол между двумя векторами и находится по формуле .

Если отрезок разделен точкой в отношении , то координаты точки находятся по формулам

, .

Если , то получаются формулы для нахождения координат середины отрезка:

, .

Пример

Задание: Отрезок, концы которого А(-11;1) и В(9;11), разделен в отношении 2:3:5 (от А к В). Найти точки деления.

Решение: Обозначим точки деления от А к В через С и D. По условию , , , и АС:СD:DВ=2:3:5. тогда С делит АВ в отношении ; значит 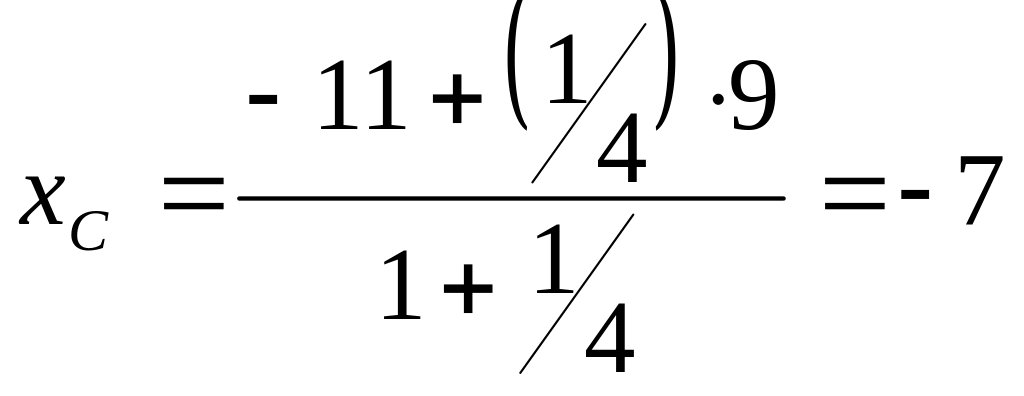; ; таким образом точка С имеет координаты (-7;3).

Точка D служит серединой АВ, поэтому ; . Тогда D(-1;6).

Задания для практической работы

1. Найдите координаты вектора , если , .

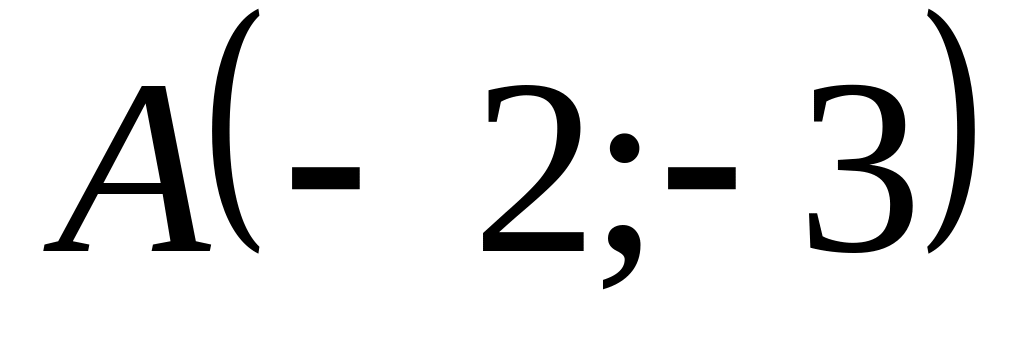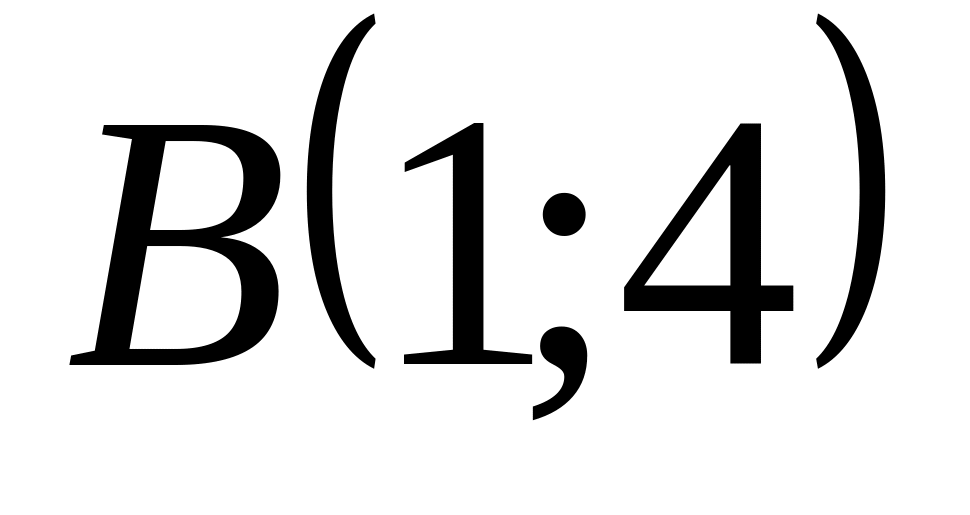2. Вычислите угол между векторами 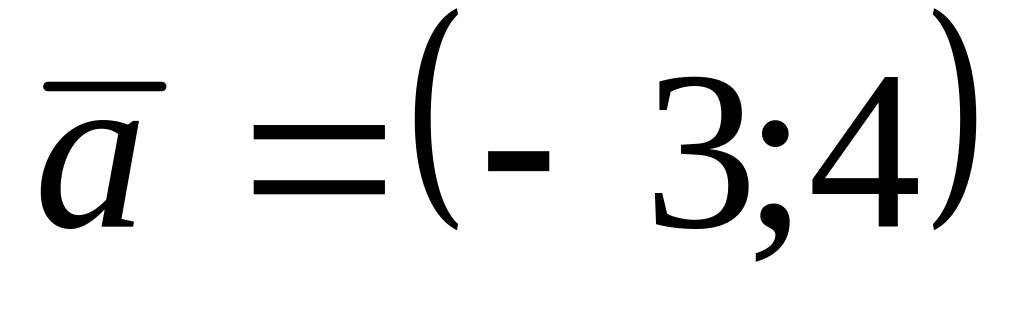и .

3. Даны векторы 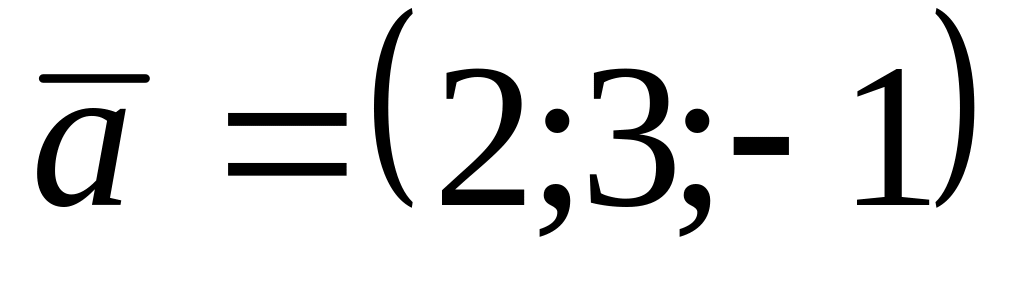, 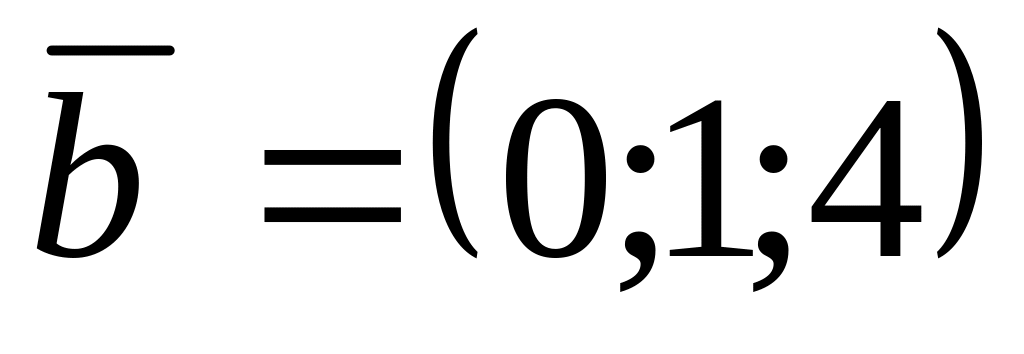и . Определите координаты вектора: а) ;

б) .

4. Расстояние от точки 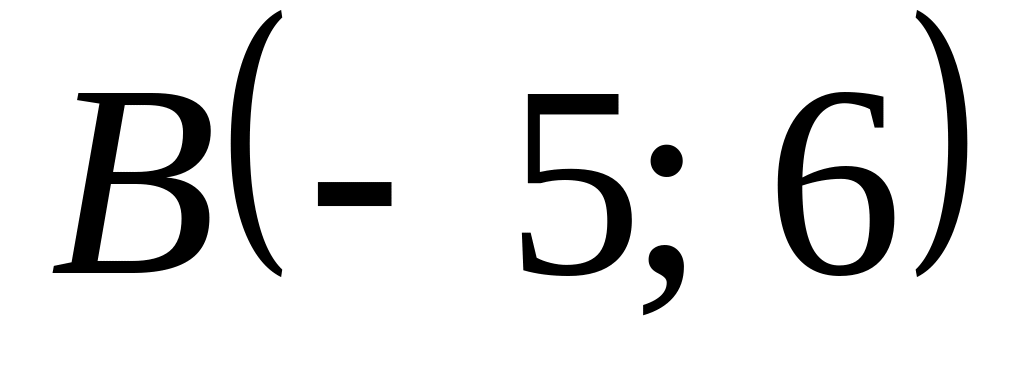до точки , лежащей на оси 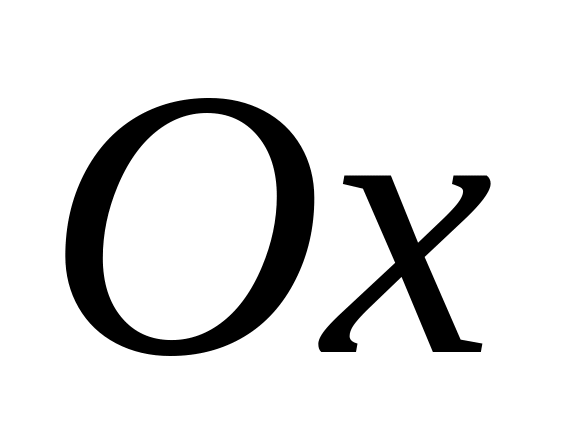, равно 10. Найдите точку .

5. Найдите скалярное произведение векторов 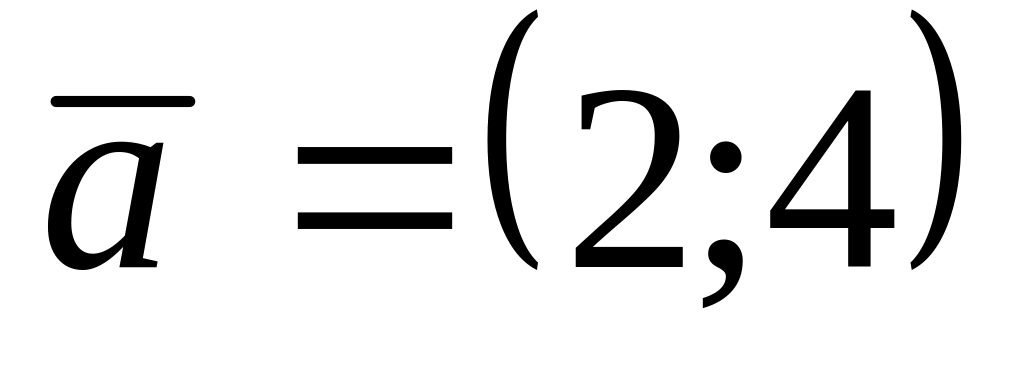и .

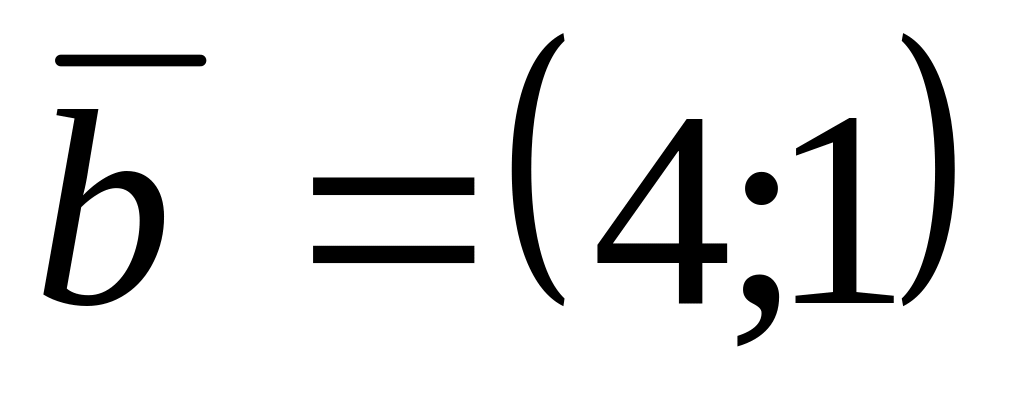6. Вычислите и , если:

1) ;

2) ;

3) ;

4) .

7. Найдите скалярное произведение векторов:

1) и ;

2) и ;

3) и ;

4) и .

Вопросы для самоконтроля:

1. Дайте определение вектора.

2. Что понимается под длиной или модулем вектора?

3. Какие векторы называются коллинеарными?

4. Как найти произведение вектора на число?

5. Что называется суммой векторов? Какие правила нахождения сумм векторов существуют?

6. Что называется разностью двух векторов? Как построить разность двух векторов?

7. Дайте определение скалярного произведения двух векторов?

8. По какой формуле вычисляется скалярное произведение в координатах?

9. По какой формуле вычисляется угол между двумя векторами в координатах?

Рекомендуемая литература: 1.1, 1.2, 1.3, 1.4, 1.5, 2.1, 2.3, 2.4, 2.5