Задания для практической работы

1. Для матрицы третьего порядка 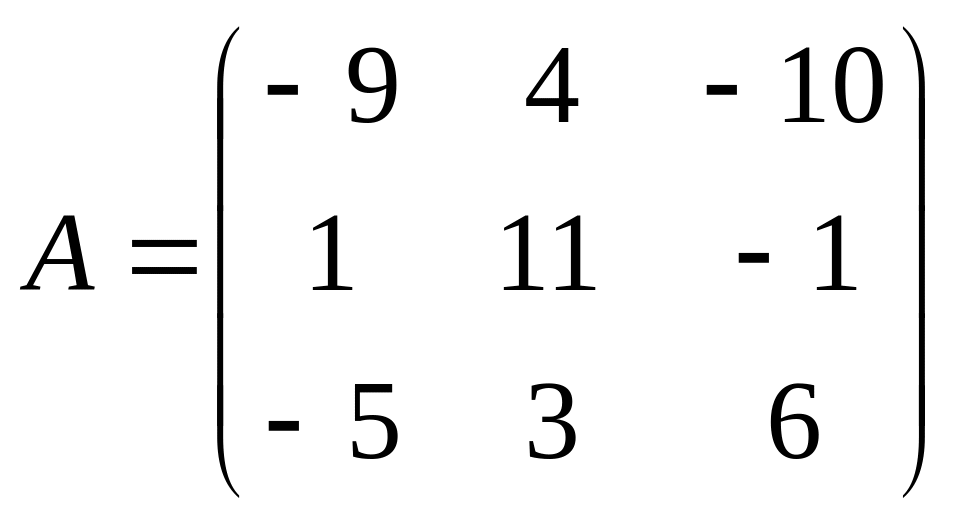найдите обратную матрицу 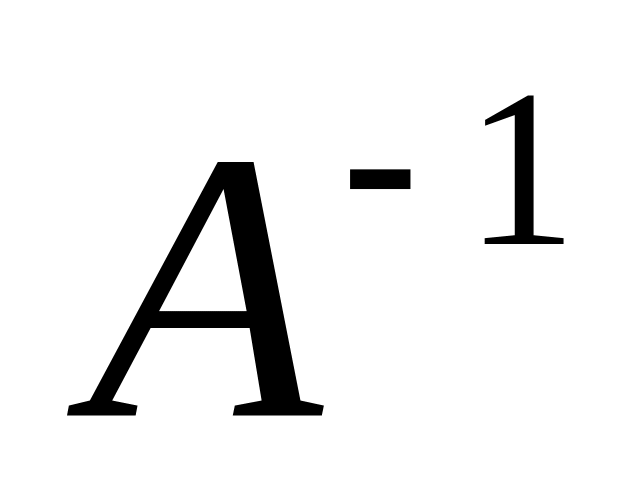. Проверьте, верно, ли она найдена.

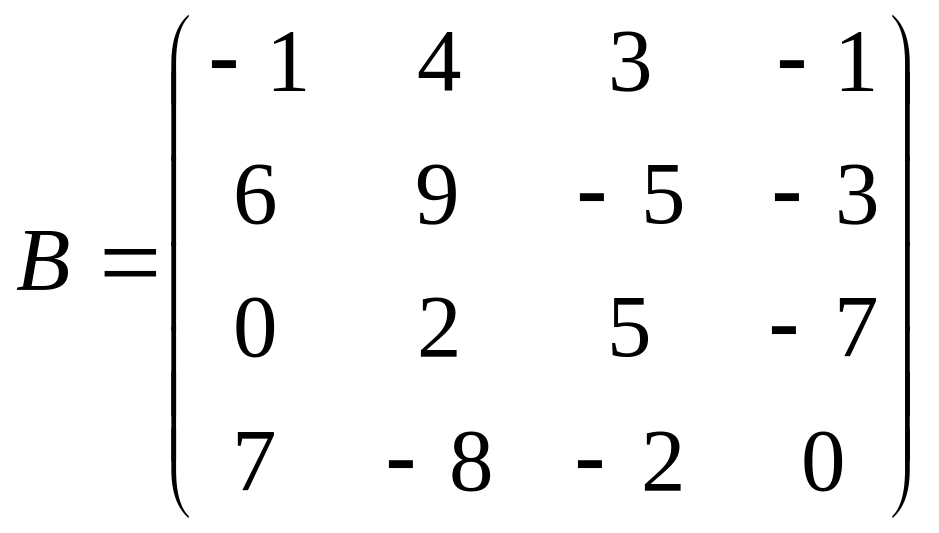2. Для матрицы четвертого порядка найдите обратную матрицу . Проверьте, верно, ли она найдена.

Вопросы для самоконтроля:

1. Какая матрица называется квадратной?

2. Какая матрица называется единичной, верхнетреугольной, нижнетреугольной, диагональной?

3. Дайте определение обратной матрицы. Всегда ли существует обратная матрица?

4. Как найти обратную матрицу?

5. Как произвести проверку обратной матрицы?

Рекомендуемая литература: 1.2, 1.3, 1.4, 2.1, 2.3, 2.5

Практическая работа №3 Тема: Решение систем алгебраических уравнений по правилу Крамера и матричным методом

Цель: Формирование навыков решения СЛАУ по правилу Крамера и матричным методом.

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Пример

Задание: Показать, что система имеет единственное решение и найти его двумя способами: а) по правилу Крамера; б) матричным методом.

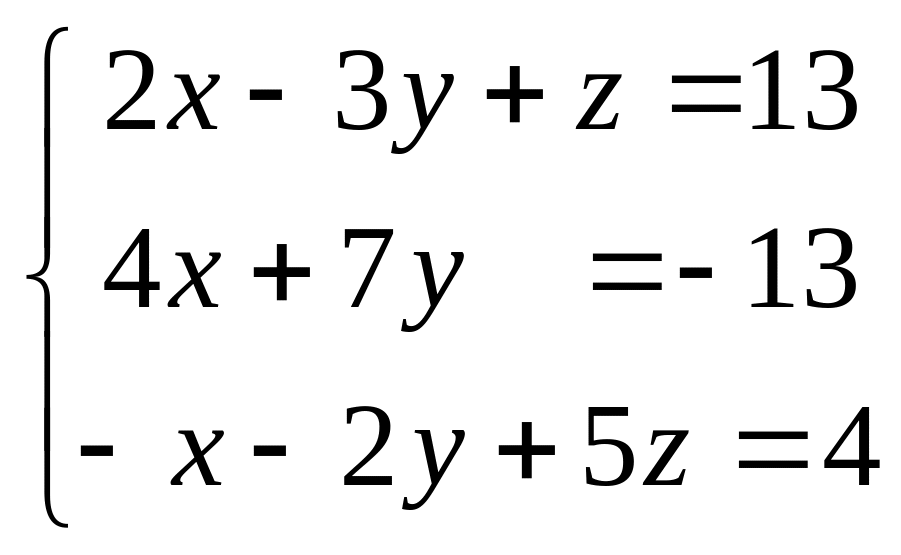
Решение: Данная система имеет размер (три уравнения и три неизвестных). Составим матрицу из коэффициентов при неизвестных:

. Матрица квадратная . Вычислим определитель матрицы , используя формулу его разложения по элементам первой строки:

.

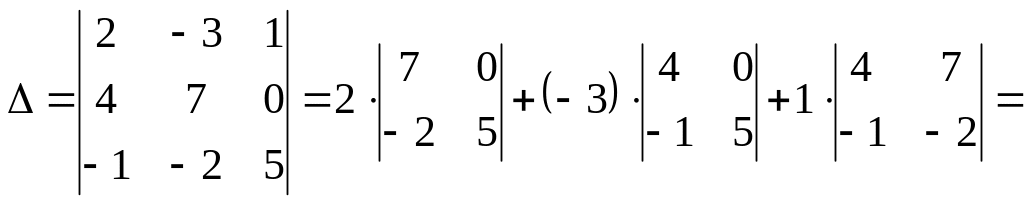
Так как определитель системы , то данная система имеет единственное решение. Это решение можно найти по правилу Крамера: ; ; , где - главный определитель системы; , , - вспомогательные определители, которые получаются из главного путем замены соответствующего столбца на столбец свободных членов, и вычисляются аналогично определителю .

;

;

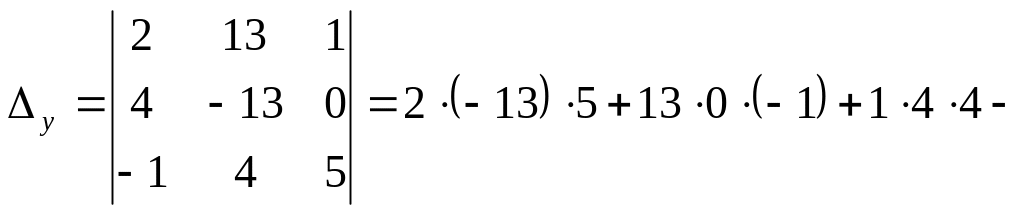
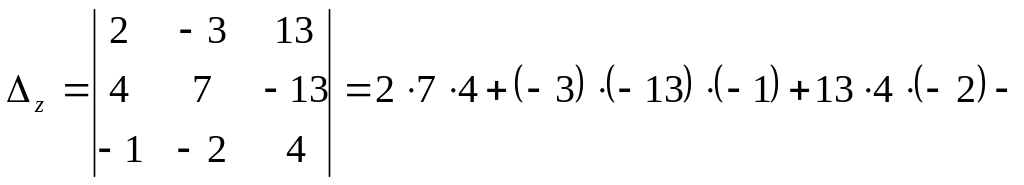
Отсюда по правилу Крамера имеем:

; ;

.

Решение системы единственно, это совокупность чисел .

Проверка: Подставим найденное решение во все уравнения исходной системы линейных алгебраических уравнений.

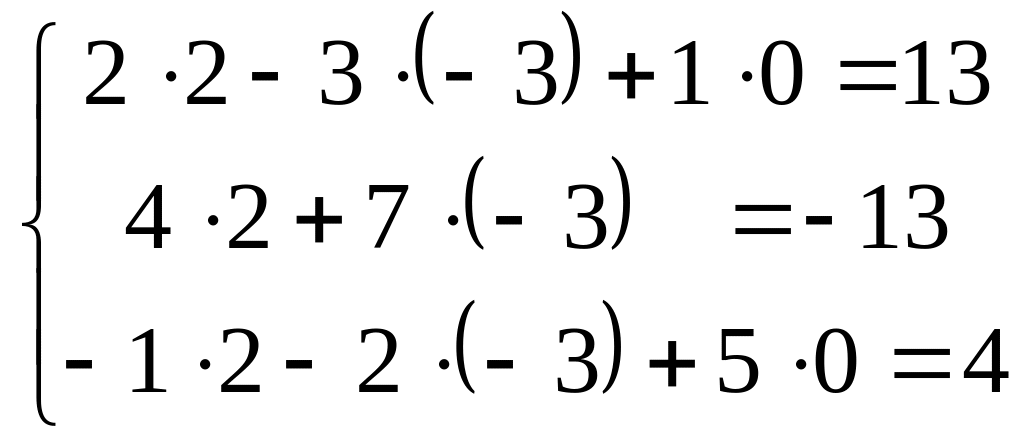
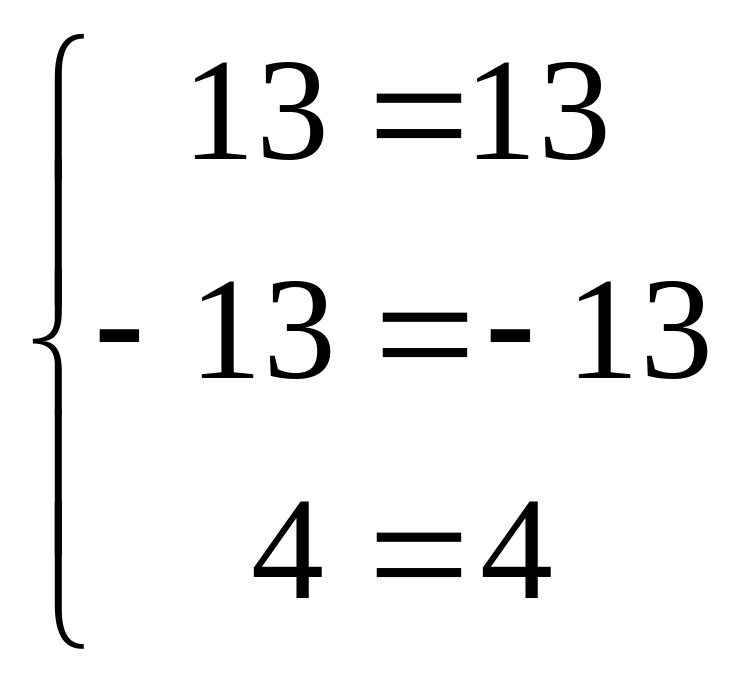
Так как все уравнения системы обратились в равенства, то решение найдено верно.

Ответ: .

Решим данную систему матричным способом. Рассмотрим матрицы:

; ; ;

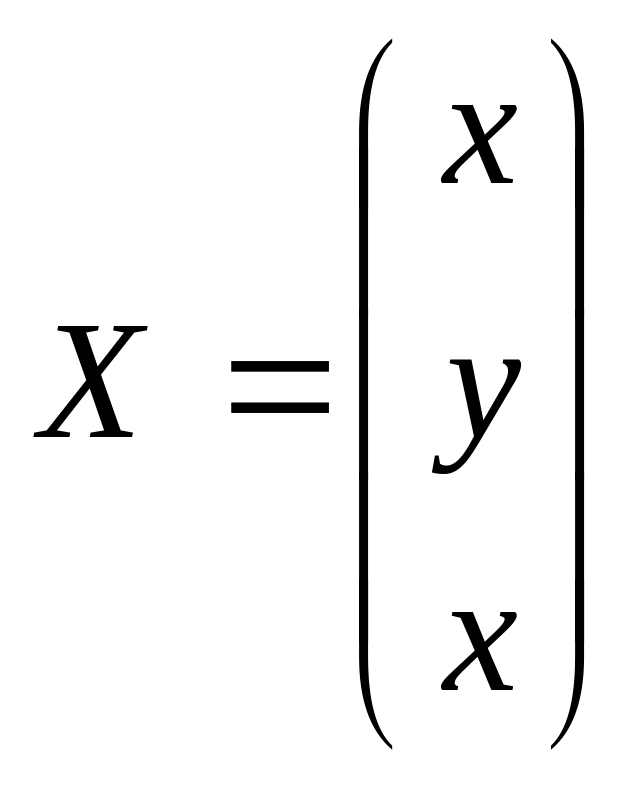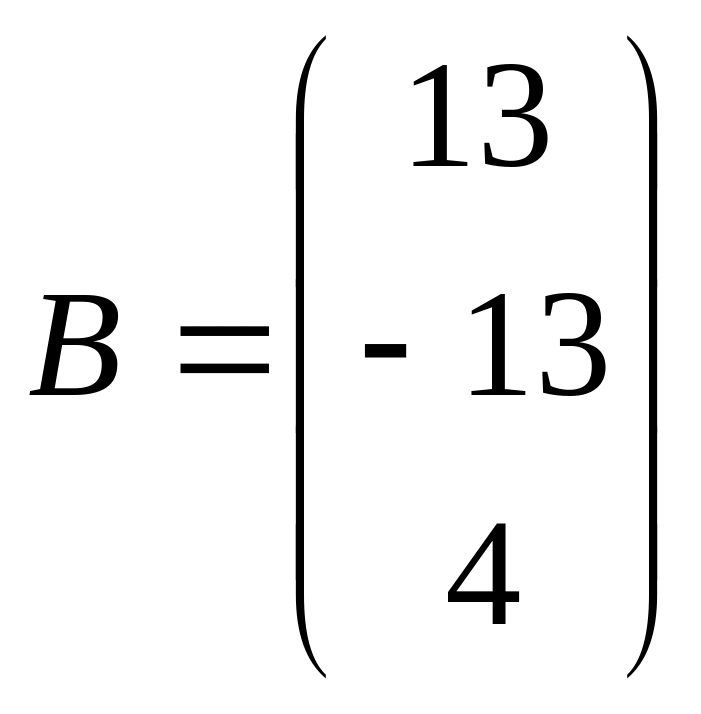- матрица коэффициентов при неизвестных, - матрица – столбец неизвестных, - матрица – столбец свободных членов.

Данную систему можно записать в виде:

;

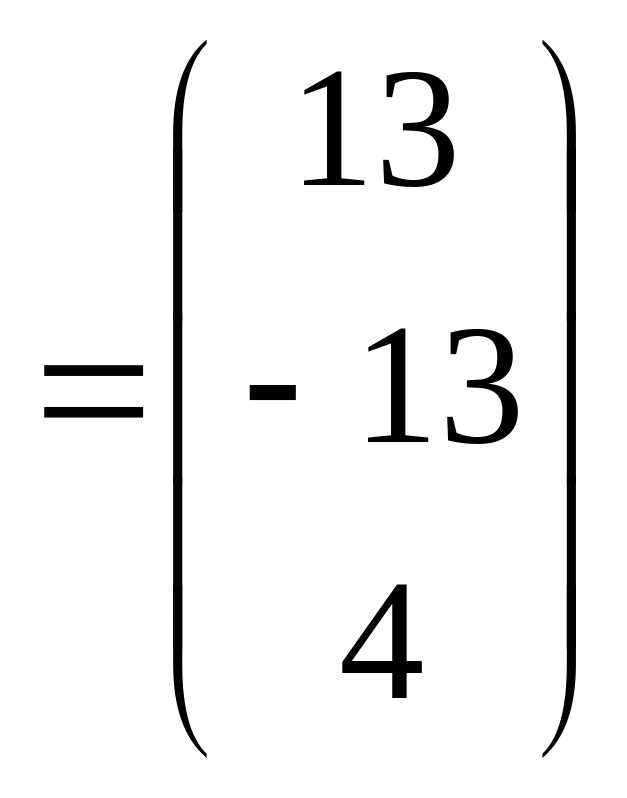При умножении матриц каждая строка матрицы умножается на столбец матрицы и в результате получается соответствующий элемент матрицы . Таким образом, последняя матричная запись содержит все три уравнения данной системы линейных алгебраических уравнений. Коротко ее можно записать так:

(3.1)

Рассмотрим матрицу , обратную к матрице . Это такая матрица, которая при умножении на данную матрицу дает единичную матрицу : , где .

Умножая обе части матричного равенства (3.1) на матрицу слева, получим:

,

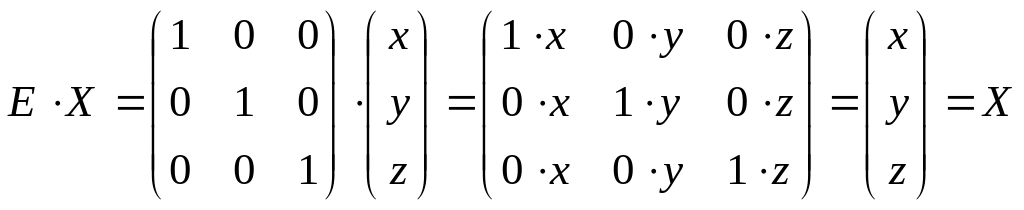, и окончательно имеем:

(3.2)

Формула (3.2) используется для нахождения решения системы линейных алгебраических уравнений. Предварительно нужно вычислить обратную матрицу. Обратная матрица вычисляется по формуле: (3.3), где - алгебраическое дополнение всех элементов матрицы ,

- главный определитель системы .

В нашем примере .

Найдем теперь алгебраические дополнения для всех элементов матрицы :

; ;

; ;

; ;

; ;

.

Составим матрицу алгебраических дополнений:

.

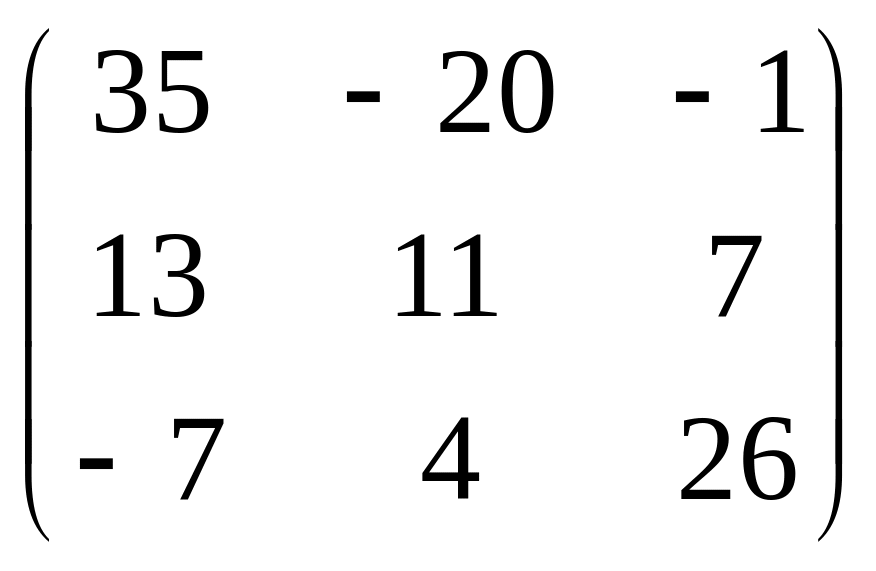Транспонируем ее, то есть поменяем местами столбцы и строки с одинаковыми номерами:

.

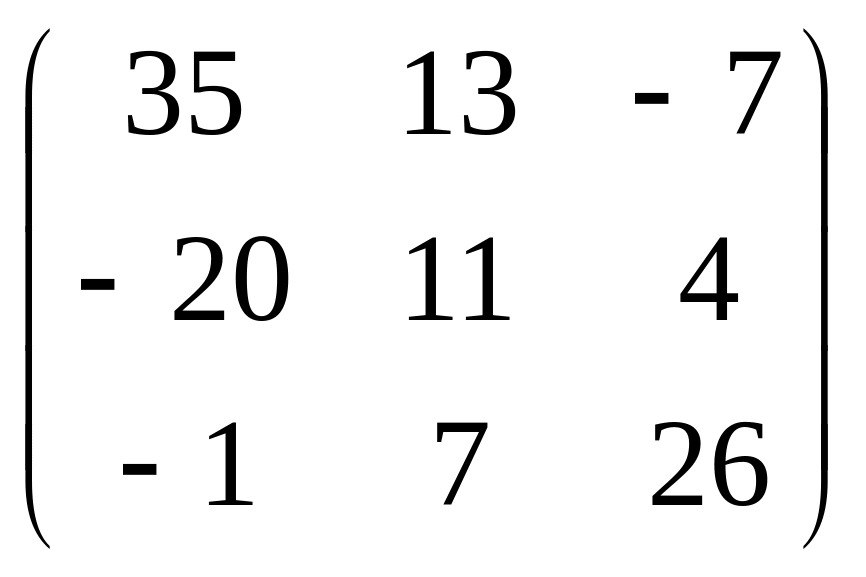Обратную матрицу получим по формуле (3.3), умножая каждый элемент последней матрицы на число, равное :

.

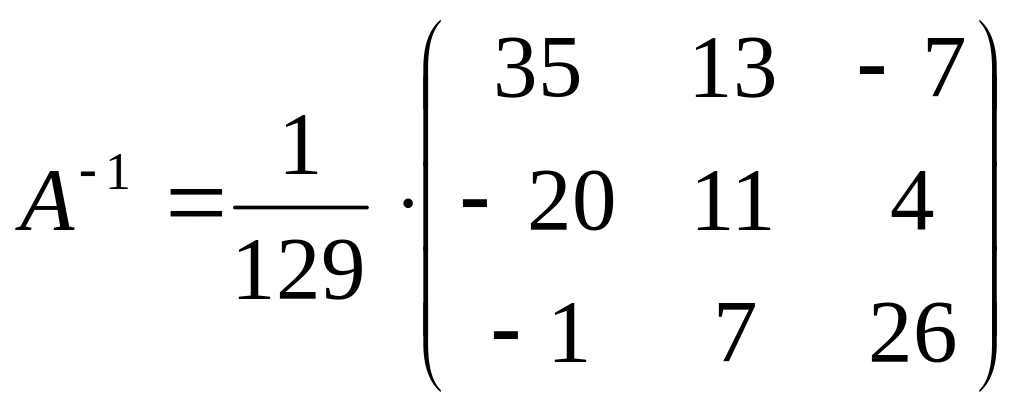Решение системы линейных алгебраических уравнений находим по формуле (3.2) умножением матрицы на матрицу свободных членов :

=

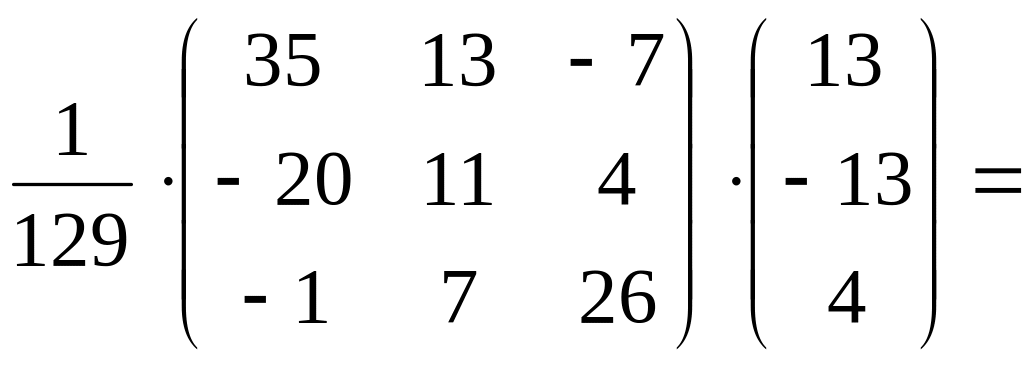
Отсюда следует, что , , .

Найденное решение было проверено выше, и совпадает с результатом, полученным по правилу Крамера.

Ответ: - единственное решение системы.