Урок 2 «Алгоритми. Властивості алгоритмів. Форми подання алгоритму . Базові алгоритмічні структури.»

1.2.1. Поняття алгоритму

Люди щоденно користуються різноманітними правилами, інструкціями, рецептами, що складаються з певної послідовності вказівок. Деякі з них настільки увійшли до нашого життя, що ми виконуємо їх, майже не замислюючись. Іноді кажуть, автоматично. Наприклад, для приготування яєчні з n яєць на вершковому маслі на електричній плиті потрібно діяти таким чином:

1. Поставити сковороду на плиту.

2. Покласти на сковороду шматочок вершкового масла.

3. Увімкнути конфорку.

4. Почекати, поки масло на сковороді розтане.

5. Кожне з n яєць розбити, а його вміст вилити на сковороду.

6. Посолити.

7. Почекати, поки загусне білок.

8. Вимкнути конфорку.

Такий запис послідовності вказівок називають алгоритмом.

Алгоритм — це запис скінченої послідовності вказівок, виконання яких призводить до розв’язання певної задачі.

Вказівка (алгоритму) — це спонукальне речення, що вказує, яку дію має виконати виконавець алгоритму.

Виконавець (алгоритму) — це жива істота (людина або тварина) або автоматичний пристрій (робот, електронна обчислювальна машина тощо), спроможна діяти відповідно з алгоритмом.

Система вказівок виконавця — це множина (сукупність) всіх вказівок, які може виконувати даний виконавець.

Середовище виконання алгоритму — об’єкти, з якими працює виконавець у процесі виконання алгоритму.

1.2.2. Властивості алгоритмів

До основних властивостей алгоритмів відносяться такі.

1. Визначеність (детермінованість) передбачає, що всі вказівки алгоритму мають бути чітко сформульованими й такими, щоб потенційні виконавці їх розуміли однозначно. Чітко визначеним має бути також порядок виконання вказівок.

2. Дискретність полягає в тому, що інструкції алгоритму виконуються покроково. Перехід до чергового кроку може відбуватися лише після виконання попереднього. Так, в алгоритмі, який наведено в прикладі розділу 2.1, вказівка 3 може бути виконана тільки після завершення дій, визначених вказівкою 2.

3. Результативність означає, що коли вхідні дані належать області допустимих значень, алгоритм має завершити роботу за скінчену кількість кроків і видати правильний результат. Якщо ж вхідні дані не належать області допустимих значень, то алгоритм або не завершить свою роботу, або завершить, але буде отримано неправильний розв’язок задачі. Результатом роботи алгоритму може стати також повідомлення про те, що задача розв'язання не має. Зазначимо, що у разі повторного виконання алгоритму для одних і тих самих вихідних даних послідовність виконання вказівок, а також результати мають залишитися незмінними.

4. Масовість означає, що алгоритм призначений для розв'язування не однієї конкретної задачі, а певного класу однотипних задач. Вихідні дані в однотипних задачах можуть бути різними, але вони не мають виходити за межі допустимого діапазону.

5. Формальність. Різні виконавці алгоритму мають отримувати одні й ті самі результати. Будь-яка команда, виконана багато разів одним або різними виконавцями, за одних і тих самих вихідних даних завжди має приводити до одного результату. Після виконання кожної команди (вказівки) виконавець має знати, яку команду необхідно виконувати наступною.

Як правило, команди виконуються послідовно у порядку їхнього запису. Якщо команди мають виконуватися непослідовно, про це зазначається у спеціальній вказівки.

Приклад. Опишемо алгоритм розв'язування квадратного рівняння.

1. Присвоїти змінним a, b і c певні числові значення.

2. Обчислити значення дискримінанта d за формулою: d= b²–4ac.

3. Якщо d<0, перейти до пункту 6, інакше виконати пункт 4.

4. Визначити x₁ і x₂ за формулами:

5. Перейти до пункту 7.

6. Дискримінант від'ємний. Рівняння розв’язків не має.

7. Кінець.

Приклад. Алгоритм обчислення найбільшого спільного дільника двох натуральних чисел A і B (алгоритм Евкліда).

1. Якщо A=B, то перейти до пункту 7, інакше виконати пункт 2.

2. Якщо A>B, то перейти до пункту 5, інакше виконати пункт 3.

3. Значення B зменшити на величину A.

4. Перейти до пункту 1.

5. Значення A зменшити на величину B.

6. Перейти до пункту 1.

7. Найбільший загальний дільник, який має значення A, присвоїти змінній D.

8. Кінець.

Неважко впевнитися, що алгоритм Евкліда дає правильний результат при різних значеннях натуральних чисел A і B. Наприклад, якщо A=23 i B=65, то D=1. Якщо A=119 i B=51, то D=17.

Слід зазначити, що міра деталізації алгоритму залежить від того, на яких виконавців він розрахований. Наприклад, для того, хто знає таблицю множення, сам запис A*B однозначно визначає послідовність дій. Для того, хто знає правило додавання, але ще не знає таблиці множення, множення двох натуральних чисел A і B може бути описано у вигляді послідовності вказівок із виконання операції додавання.

Питання для самоперевірки знань

1. Які основні властивості має алгоритм?

2. В якому порядку виконуються вказівки алгоритму?

3. Чи можуть різні виконавці отримати різні результати роботи одного алгоритму?

4. Від чого залежить міра деталізації алгоритму?

1.2.3. Способи опису алгоритмів

Існують різноманітні способи опису алгоритмів, наприклад, словесно-формульний опис, зображення у вигляді блок-схеми, запис мовою програмування тощо. Розглянемо два найбільш поширених простих способи.

Словесно-формульний спосіб. Цей спосіб опису алгоритмів люди широко використовують у повсякденному житті під час запису інструкцій з експлуатації пристроїв, рецептів виготовлення ліків тощо. Форма запису вказівок довільна. Головне, щоб вказівки були точними та зрозумілими всім користувачам. Перевага цього способу полягає в його простоті. Але такі описи алгоритмів часто є громіздкими, а їхні вказівки можуть сприйматися різними виконавцями не однозначно.

Для наочності і компактності запису алгоритмів у словесно-формульному вигляді використовується оператор присвоювання, що позначається символами «:=». Структура цього оператора є такою: <змінна>:=<вираз>

Під час виконання оператора присвоювання спочатку обчислюється значення виразу, розташованого праворуч від символів «:=», а потім отримане значення присвоюється змінній, записаної ліворуч.

Приклад. За допомогою оператора присвоювання алгоритм розв'язування квадратного рівняння (див. підрозділ 1.2.2) можна записати так:

1. Ввести значення змінних a, b, c.

2. d:=b²–4ac.

3. Якщо d<0, виконати пункт 6, інакше — пункт 4.

4. 

5. Перейти до пункту 7.

6. Дискримінант від’ємний. Рівняння розв'язків не має.

7. Кінець.

Зображення алгоритмів у вигляді блок-схеми. Переваги зображення алгоритму блок-схеми, порівняно зі словесно-формульним способом опису, полягають у наочності та простоті. Основні графічні позначення, за допомогою яких конструюються блок-схеми алгоритму, наведені на рис. 1.2.1.

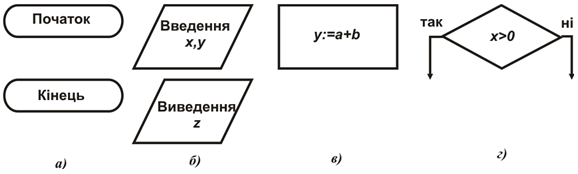
Рис. 1.2.1. Основні графічні позначення на блок-схемах: термінатор (а); дані (б); процес (в); розгалуження (г)

1. Термінатор (рис. 1.2.1, а). Визначає початок або кінець алгоритму. У середині закругленого прямокутника може записуватися слово ”Початок” або ”Кінець”. Крім того, разом зі словом ”Початок” може бути вказано ім’я алгоритму або дія, яку він виконує.

2. Дані (рис. 1.2.1, б). Конструкція відображує дані, що можуть бути записані на різноманітних носіях. Може використовуватися для позначення операцій введення і виведення. У цьому випадку всередині паралелограма слід записувати слово ”Введення” (”Виведення”) і значення або імена змінних, що вводяться (виводяться).

3. Процес (рис. 1.2.1, в). Конструкція відображує процес обробки даних будь-якого типу (виконання певної операції або ж групи операцій). На кожний блок процесу можуть вказувати одна або декілька стрілок, а виходити з нього може тільки одна стрілка.

4. Розгалуження (рис. 1.2.1, г). Конструкція розгалуження використовується з метою перевірки виконання певної умови і розгалуження обчислювального процесу залежно від результатів цієї перевірки. Всередині ромба записується умова, яка, власне, й перевіряється. Якщо така умова є істинною, то надалі обчислювальний процес здійснюється гілкою "так", у протилежному випадку – гілкою "ні". Вказувати на конструкцію розгалуження можуть декілька стрілок, а виходити з неї можуть дві стрілки.

Всі конструкції блок-схеми алгоритму з'єднуються стрілками, які визначають порядок виконання дій. Замість стрілок, що спрямовані згори донизу або зліва направо, можуть зображуватися лінії. Якщо декілька стрілок спрямовано в один блок, їх можна поєднати в одній точці.

Приклад. Сконструюємо блок-схему алгоритму обчислення значення виразу

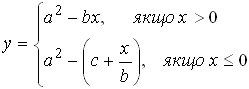
Значення виразу залежить від чотирьох параметрів: а, b, c, x. Тому після термінатора , що позначає початок алгоритму, зобразимо блок даних, у якому встановлюватимуться значення цих параметрів. Вираз є умовним, адже те, за якою формулою обчислюватиметься значення y, залежить від виконання умови x>0. Тому після блоку даних зобразимо розгалуження, на кожній з гілок якого розташуємо блоки процесу, де запишемо відповідні формули. За якою формулою не обчислювалося б значення y, його необхідно вивести. Отже обидва блоки процесів з’єднуємо з блоком даних, яким позначимо виведення y. Завершуємо блок-схему термінатор «Кінець» (рис. 1.2.2).

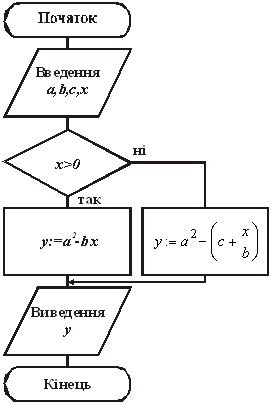
Рис. 1.2.2. Блок-схема алгоритму обчислення значення умовного виразу