3. Знакопочережні ряди.

Визначення.

Знакопочережним рядом називається знакозмінний ряд із чергуванням знаків елементів.

Припустимо, що ряд починається з і трохи змінимо позначення

(5)

Тут чергування знаків елементів замінено чергуванням знаків дій, а самі елементи вже додатні:

Теорема (ознака Лейбніца)

Якщо для ряду (5) і , то ряд (5) збігається.

Приклад.

.

Ряд збігається за ознакою Лейбніца.

4. Наслідок

Якщо знакопочережний ряд збігається і S - його сума, то для будь-якого n виконана нерівність

.

Цей наслідок знаходить застосування в наближених обчисленнях для оцінки похибки при заміні суми ряду його частковою сумою.

Контрольні питання

1. Якою є інтегральна ознака збіжності?

2. Як застосовується інтегральна ознака збіжності?

3. Що таке абсолютна збіжність знакозмінного ряду?

4. Які ряди називаються умовно збіжними?

5. Що називається знакопочережним рядом?

6. Як застосовується ознака Лейбніца?

Лекція 3

Функціональні ряди

1. Функціональні ряди. Область збіжності.

2. Рівномірно збіжні ряди.

3. Степеневі ряди.

4. Теорема Абеля.

5. Радіус і інтервал збіжності степеневого ряду.

1. Визначення Функціональним рядом називається нескінчена сума функцій

(1)

Ряд (1) називається збіжним у точці , якщо збігається відповідний числовий ряд (2)

(2)

Приклад.

- функціональний ряд; .

У точці , ряд збігається.

У точці , ряд розбігається.

Визначення .

Множина точок, у яких функціональний ряд збігається, називається його областю збіжності. Сума функціонального ряду є функцією, яка визначена на області збіжності.

.

Приклад (продовження)

.

Визначення.

Частковою сумою ряду (1) називається сума перших n елементів ряду.

Залишком ряду називається різниця його суми і часткової суми

За визначенням збіжності ряду на області збіжності виконане співвідношення

.

2. Визначення.

Ряд (1) називається рівномірно збіжним на відрізку , якщо для будь-якого знайдеться , такий, що при відразу для усіх .

Рівномірна збіжність функціонального ряду означає збіжність у всіх точках відрізка з однаковою швидкістю.

Ознака Вейєрштрасса (рівномірної збіжності)

Якщо існує збіжний числовий знакододатний ряд і виконана нерівність для , то ряд збігається рівномірно на .

Приклад.

- збіжний числовий ряд; ; отже, вихідний ряд збігається рівномірно на відрізку .

Властивості рівномірно збіжних рядів

1. Якщо усі безперервні на і (1) збігається рівномірно на , то його сума є безперервною функцією на .

2. У тих же умовах ряд (1) можна почленно інтегрувати на .

3. Якщо 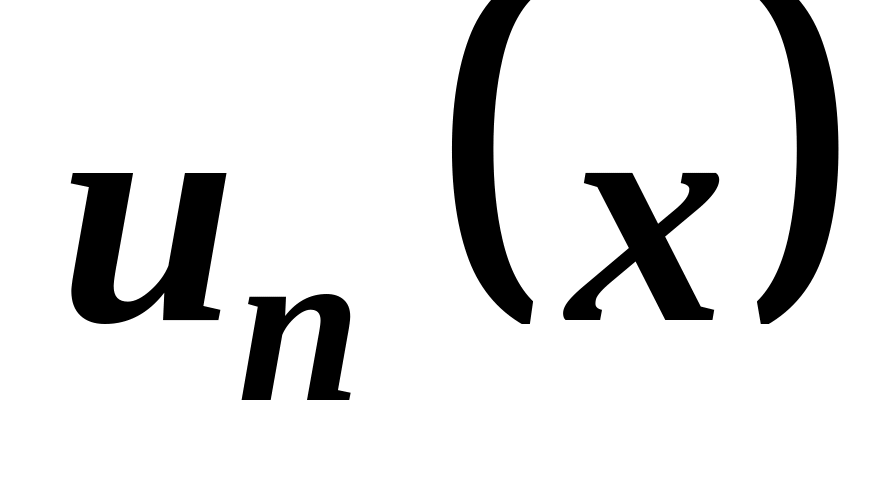- диференційовані на , і ряд 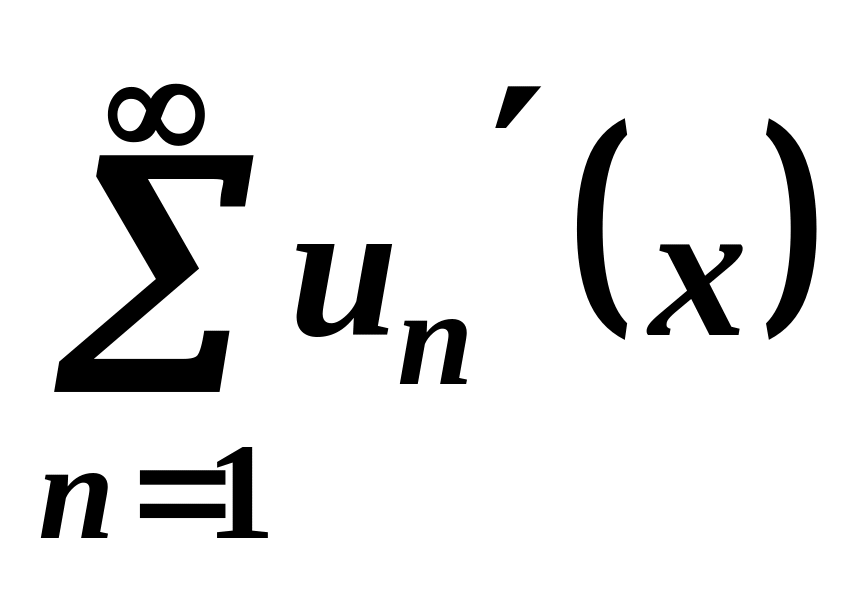збігається рівномірно на , то виконана рівність

3. Степеневі ряди

Визначення.

Степеневим рядом називається функціональний ряд наступного вигляду

(3)

Тут

4. Теорема Абеля

1. Якщо ряд (3) збігається в точці , то він збігається для всіх , що задовольняють нерівності .

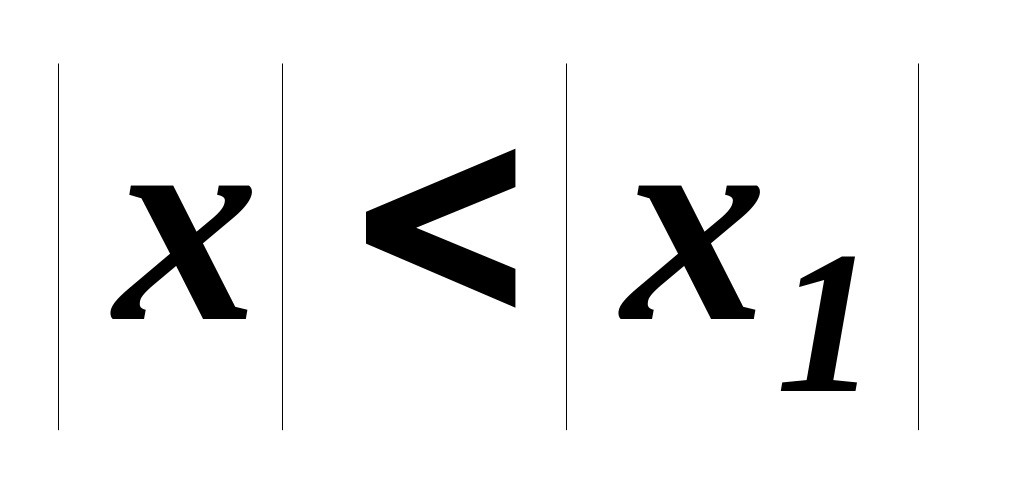2. Якщо ряд (3) розбігається в точці , то він розбігається для усіх , таких що .

В иникає задача знаходження межі між точками збіжності і розбіжності.