Цель (человека)

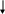
ЗАДАЧИ (инструмента)
Экспертная Что будет (было), если…	Конструктивная Как сделать, чтобы…

Инструмент – МОДЕЛЬ (отображение свойств объекта)
Познавательная	Прагматическая

Рис. 1.1 Соотнесение цели, задач и моделей

По степени абстрагирования от оригинала модели делятся на два больших класса: физические (аналоговые) и математические.

Физические модели (макеты), классификация которых приведена на рис.1.2, предполагают реальное воплощение свойств оригинала. Например, при проектировании самолета создается его макет, обладающий теми же аэродинамическими свойствами; при планировании застройки изготавливается архитектурный макет; аналоговая модель Земли – глобус.

Р ис.1.2 Классификация физических моделей

Математические модели представляют собой формализованное описание системы (процесса) с помощью некоторого абстрактного языка, например, в виде совокупности математических отношений или схемы алгоритма. По большому счету любое математическое выражение, в котором фигурируют физические величины, можно рассматривать как математическую модель. Например, S=v*t – модель равномерного прямолинейного движения. Элементы математического моделирования возникли на самых ранних этапах зарождения математики.

В зависимости от метода исследования математические модели разделяют на: аналитические, численные и имитационные.

Аналитическая модель – это точное формализованное описание системы, которое позволяет получить решение в явном виде, используя математический аппарат.

Численная модель допускает только частичные численные решения для конкретных начальных условий и количественных параметров модели.

Имитационная модель – это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений. Причем алгоритмы и правила не дают возможности реализации с помощью математических аналитических и численных методов, но сами алгоритмы позволяют имитировать процесс функционирования системы и производить измерения интересующих характеристик.

В зависимости от степени детализации математические модели разделяют на микро-, макро- и мета- уровневые (рис.1.3).

Математическая модель на микроуровне отражает процессы в непрерывном пространстве и непрерывном времени. На макроуровне уровне происходит дискретизация пространства по функциональному признаку, но для непрерывного времени. На метауровне в качестве элементов системы выступают сложные совокупности деталей.

1.2. Общие вопросы моделирования систем

В общем случае объектом-оригиналом может быть некоторая естественная или искусственная система. Любая система состоит из компонентов и связей между ними, а также их связей с внешней средой.

Компонент (элемент) системы – один из объектов, входящих в систему. Он осуществляет некие преобразования входов в выходы. Входы и выходы могут быть пространственными и временными, причем временной вход есть причина, а временной выход – следствие. Например, у объекта «проводник», пространственный вход электрического тока – обмотка генератора, а выход – потребляющее устройство. Временной же вход в него – это напряжение, а выход – ток.

Законы преобразования входов компонента в выходы называются функцией компонента, а сам процесс преобразования – его функционированием. Например, функцией проводника может быть передача электрической энергии от источника к потребителю, или величина тока, которую пропускает проводник при данном напряжении.

Функция может быть описана количественно. Тогда говорят о математической функции. Например, для количественного описания проводника с током нужно математически выразить зависимость силы тока от напряжения: I=f(U), где I – сила тока, U—напряжение. Для простого проводника такая функция линейна и называется законом Ома: I=U/R, где R – сопротивление. Для полупроводников эта математическая функция носит более сложный характер. Математическая функция – основной инструмент математического моделирования систем. Математическая модель в этом случае есть система взаимосвязанных математических функций, призванная решить задачу «каково будет значение одних параметров при определенном значении других».

Связь, с точки зрения структуры системы, формирует эту самую структуру. С точки зрения функционирования системы, она преобразует выход одного компонента во вход другого. Основное ее отличие от компонента заключается в том, что это преобразование тривиально. То есть, если компонент существенно изменяет поток, то связь его существенно не изменяет. Например, провод в радиоприемнике существенно не изменяет протекающий через него ток, а вот транзистор – изменяет. Поэтому транзистор будет компонентом, а провод – связью.

В зависимости от задачи один и тот же объект можно моделировать как компонент, а можно – как связь. (Моделирование радиоприемника, моделирование энергосистемы – объект «провод»).

Связи также могут быть пространственными (структурными) и временными (причинно-следственными). Структурные связи обеспечивают порядок в пространстве, в то время как причинно-следственные – порядок во времени. Это всегда следует учитывать при моделировании систем: любая система имеет как пространственную структуру (сетка структурных связей), так и временную (сетка причинно-следственных связей), и они взаимно определяют друг друга.

Модели систем, как правило, многоуровневые. Простейший уровень модели – модель «черного ящика». Это модель, не рассматривающая внутреннее устройство системы, а описывающая только внешние связи и функции системы. По внешним данным «черного ящика» и его реакции на внешние воздействия можно судить о его внутреннем устройстве, но суждение будет ненадежным, особенно для предсказания поведения системы в различных условиях.

Если начинать забираться внутрь «черного ящика», то модель системы становится иерархической. Теперь это уже набор некоим образом взаимосвязанных «черных ящиков». Поскольку все системы иерархичны, в каждый «черный ящик» можно углубляться; модели, состоящие из нескольких «черных ящиков» можно компоновать и создавать, таким образом, многоуровневые модели.

Все модели систем (в т.ч. и «черного ящика») делятся на два принципиально разных типа: статические и динамические. Статические модели не описывают процесс функционирования системы. Это, как правило, структурная модель, описывающая элементы с их характерами, системообразующие связи и потоки, идущие по этим связям (например, чертеж изделия, электрическая схема и т.п.). Динамическая модель описывает зависимость изменения различных свойств системы от времени, а также от начальных и граничных условий. Тем самым, динамическая модель отображает причинно-следственные связи.

О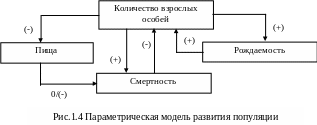 дин из частных случаев динамической модели – параметрическая модель, описывающая влияние различных параметров системы друг на друга. Параметрическая модель оказывается очень ценной для предсказания развития системы при изменении внешних параметров. Параметрическая модель состоит из различных параметров, связанных взаимным влиянием. При этом влияние может выражаться математически с различной степенью строгости. Оно может выражаться математическим выражением, а может только знаком влияния: (+), если исходный параметр приводит к увеличению конечного ( чем больше исходный, тем больше конечный); (-) – к уменьшению (больше исходный – меньше конечный).

Параметрическая модель не обязательно соответствует структурно-функциональной. Например, одному элементу структурной модели может соответствовать несколько параметров и т.п. На рис.1.4 приведена упрощенная параметрическая модель популяции в условиях неограниченного ресурса пищи.