7.7. Моделирование смо по событиям

Данный алгоритм относится к классу алгоритмов моделирования по событиям. Это означает, что модельное время в процессе моделирования изменяется скачками от одного события к другому. Событиями в рассматриваемой СМО являются моменты прихода заявок извне и моменты освобождения каналов обслуженными заявками. Поэтому модельное время всегда равно моменту прихода очередной заявки или освобождения канала и всегда изменяет свое значение на момент наступления ближайшего события из перечисленных.

Д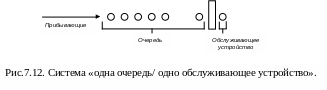 ля упрощения рассмотрим возможный подход к моделированию одноканальной СМО с ограниченной очередью (рис.7.12).

Функционирование такой очереди определяется следующими характерными особенностями и предположениями:

1) имеется случайная переменная X, которая определяет время прибытия следующего клиента. Существует несколько возможностей для решения вопроса о времени прибытия клиента. Будем предполагать, что если клиент K прибывает в момент времени t, то клиент K+1 прибывает в момент t+T, где Т – случайная переменная, значение которой лежит между 0 и некоторым фиксированным числом MAXТ, с заданным распределением вероятностей (экспоненциальным).

2) имеется случайная переменная S, определяющая, сколько времени длится обслуживание клиента K. Предполагается, что значение величины S лежит между 0 и некоторым другим фиксированным целым числом MAXC с заданным распределением вероятностей. Если обслуживание начато, оно продолжается до полного завершения, т.е. не допускается прерывание или обслуживание с приоритетом.

3) существует очередь клиентов, обслуживаемая по принципу: первым пришел – первым обслужен (FIFO). Как только клиент встает в очередь, он останется в ней, пока не будет обслужен. Сразу после обслуживания он покидает систему.

4) Все действия в системе описываются дискретными событиями. Говорят, что событие является первичным или независимым, если оно не вызвано другим событием; в противном случае оно называется вторичным или условным событием. Независимыми событиями в системе обслуживания являются: (а) – прибытие клиента и (б) – завершение обслуживания клиента.

5) в начальном состоянии система пуста. В момент времени t=0 обслуживающее устройство не занято и в очереди никого нет.

6) для определения промежутков времени между прибытиями клиен­тов и продолжительностей их обслуживания применяется датчик случайных чисел. Фактически во всех вычислительных устройствах имеется системный датчик случайных чисел для равномерного распределения на интервале [0,1). Как уже отмечалось выше, это распределение может быть использовано для того, чтобы смоделировать другие распределения случайной переменной.

Большинство систем обслуживания имеют заранее установленный неизменный порядок (правила) очереди. Поэтому для таких систем этот вопрос не входит в задачу разработки имитационного алгоритма. Но в других случаях, таких, как операционные системы ЭВМ, определение оптимальных порядков очереди — важная цель моделирования.

Основное предположение в системах с дискретными событиями заключается в том, что состояние системы изменяется, только когда происходит событие; в противном случае состояние остается неизменным. Таким образом, нет нужды в непрерывном ходе часов, когда ничего не случается. Наиболее общий подход – произвести все изменения, необходи­мые вследствие совершившегося события, а затем продвинуть имитируемое время ко времени следующего события (моделирование по событиям).

Д ля иллюстрации этого подхода на рис.7.13 представлена принципиальная блок-схема алгоритма моделирования системы одна очередь/одно обслуживающее устройство.

Чтобы получить моделирующую программу, необходима некоторая переработка этой блок-схемы. В частности, на рис.7.13 нет условия для остановки (или возвращения). С этой целью вводятся три различные переменные ARР, COMP и TERM, обозначающие соответственно время следующего прибытия, время завершения обслуживания и время окончания моделирования. Также вводится переменная СLОСК для записи текущего времени. Для метода моделирования по событиям, полагаем переменную СLОСК равной времени следующего запланированного события: это или время следующего прибытия, или время завершения обслуживания, или время окон­чания моделирования. Тогда блоки 2, 3 и 4 становятся такими, как показано на рис. 7.14.

Далее рассмотрим, что должно быть сделано в блоке 5 на рис. 7.13, когда имеет место новое прибытие. Во-первых, можно определить время следу­ющего прибытия в соответствии с правилом вида

ARP=CLOCK+RANARR (0, MAXA)

где RANARR (0 , МАХА) — функция, которая дает случайное целое число между 0 и некоторой фиксированной константой MAXA с опреде­ленным распределением вероятностей.

С ледующая работа, которую нужно выполнить, когда прибывает новый клиент, – это или поставить клиен­та в очередь, или если обслужи­вающее устройство свободно, то обслужить его. Если очереди нет (длина очереди определяется пере­мен­ной QUEUE), то можно определить время ухода данного клиента (т. е. время полного обслу­жи­вания) из уравнения

СОМР=СLОСК+

RANСОМ(0, МАХС)

Тогда блок 5 становится таким, как на рис. 7.15.

Для завершения блока 6 также потребуется определить время завершения следующего обслуживания:

COMP=CLOCK+RANCOM (1, MAXC)

Следует, однако, рассмотреть особую ситуацию, когда очередь стано­вит­ся пустой. Конечно, в этом случае время завершения следующего обслу­жи­вания не имеет смысла. Поэтому произвольно полагаем СОМР=ТЕRМ+1, чтобы гарантировать, что завершение не является следующим запланированным событием. Тогда блок 6 становится таким, как показано на рис. 7.15.

Ч то еще осталось сделать? Во-первых, нужно задать начальные значения всем переменным, таким, как АRR, ТЕRМ, QUEUE, QMAX , МАХА, МАХС и СОМР. Затем нужно определить подпрограммы для вычисления RANARR и RANCOM. Наконец, нужно представить какой-то вывод (окружность, обозначенная Т на рис. 7.15. Эта блок-схема еще не совсем полна. Например, неорганизован сбор данных - по существу регистрируется только QМАХ.