7.3 Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний

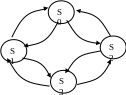
Построим размеченный граф состояний для выше рассмотренного примера (система из двух узлов, которые могут выходить из строя и ремонтироваться) – рис.7.7.

S0 – оба узла исправны

S1 – первый узел ремонтируется, второй исправен

S2 – второй узел ремонтируется, первый исправен

S3 – оба узла неисправны

Интенсивность потоков событий будем вычислять, предполагая, что среднее время ремонта узла не зависит от того, ремонтируем ли один узел или оба сразу (это будет именно так, если ремонтом каждого узла занят отдельный специалист). Найдем все интенсивности событий.

 2

 2

2 

2 

Рис. 7.7. Размеченный граф состояний системы

Пусть система находится в состоянии S0. Какой поток переведет ее в состояние S1? – Поток отказов первого узла. Его интенсивность  равна 1, деленной на среднее время безотказной работы. Какой поток событий переводит систему обратно, из S1 в S0? Очевидно, поток «окончаний ремонта» первого узла. Его интенсивность  равна 1, деленная на среднее время ремонта.

Аналогично определяются интенсивности потоков событий, переводящих систему по всем стрелкам графа.

Имея в своем распоряжении размеченный граф состояний системы легко построить математическую модель данного процесса.

Пусть рассматривается система S, имеющая n возможных состояний S1, S2, S3…Sn. Назовем вероятностью i-го состояния вероятность pi(t), того, что в момент времени t система будет находиться в состоянии Si. Очевидно, что для любого момента времени сумма всех вероятностей состояний будет равна 1:  p_i(t) =1 (i=1,n)

Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний pi(t) как функцию времени. Для этого составляются и решаются так называемые уравнения Колмогорова – особого вида дифферен­циальные уравнения, в которых неизвестными функциями являются вероятности состояний.

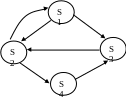
Рассмотрим на конкретном примере, как составляются такие уравнения. Пусть система S имеет 4 состояния (рис. 7.8).

_ ₁₃

₁₂

₃₂

_4 ₄₃

Рис. 7.8 Пример графа состояний системы

Рассмотрим одну из вероятностей состояний, например, p₁(t). Это – вероятность того, что в момент времени t система будет находиться в состоянии S1. Придадим малое приращение t и найдем p₁(t+t) – вероятность того, что в момент t+t система будет в состоянии S1. Как это может произойти? Это может быть достигнуто двумя способами: 1) в момент t система уже была в состоянии S1 и за время t еще не вышла из него; 2) в момент t система была в состоянии S2, а за время t перешла из него в состояние S1.

Найдем вероятность первого варианта. Вероятность того, что в момент t система была в состоянии S1 равна p₁(t). Эту вероятность нужно умножить на вероятность того, что находившись в момент t в состоянии S1 система за время t не перейдет из него ни в S2, ни в S3. Суммарный поток событий, выводящий систему из состояния S1, тоже будет простейшим, с интенсивностью __. (Примечание. При наложении (суперпозиции) простейших потоков получается опять простейший поток, так как свойства стационарности, ординарности и отсутствия последействия сохраняются). Значит, вероятность того, что за время t система выйдет из состояния S1, равна (__)*t; вероятность того, что не выйдет – (1-(__)*t).

Отсюда вероятность первого варианта p₁(t)*(1-(__)*t).

Найдем вероятность второго варианта. Она равна вероятности того, что в момент t система будет находиться в состоянии S2, а за время t перейдет из него в состояние S1, то есть она равна p₂(t)*₂₁*t.

Складывая вероятности обоих вариантов, получим

p₁(t+t)= p₁(t)*(1-(__)*t)+ p₂(t)* ₂₁*t.

Раскроем скобки, перенесем в левую часть p₁(t) и разделим обе части на t:

= _21*p₂(t) – (__)*p₁(t).

Устремим, как полагается, t к 0: t0; слева получим производную функции p₁(t).Таким образом, запишем дифференциальное уравнение

= _21*p₂(t) – (__)*p₁(t)

или, отбросив аргумент t у функций p₁, p₂:

= _21*p₂ – (__)*p₁

Рассуждая аналогично для всех остальных состояний, напишем еще 3 дифференциальных уравнения. Получаем систему (7.1) из четырех дифференци­аль­ных уравнений для вероятностей состояний:

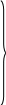
= _21*p₂ – (__)*p₁

= _12*p₁ + _32*p₃ – (_1₂₄)*p₂ (7.1)

= _13*p₁ + _43*p₄ – ₃₂*p₃

= _24*p₂ – ₄₃*p₄

Система (7.1) – система 4-х дифференциальных уравнений с четырьмя неизвест­ными функциями p₁, p₂, p₃, p₄. Заметим, что любое из них можно отбро­сить, пользуясь тем, что p₁+p₂+p₃+p₄=1. Надо выразить любое p_i через другие функции и подставить это выражение в (7.1), а соответствующее уравнение производной отбросить.

Сформулируем общее правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности какого-то (i-го) состояния. В правой части – сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженную на вероятность данного (i-го) состояния.

Запишем уравнения Колмогорова для нашего технического примера:

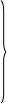= _1*p₁ + _2*p₂ – (_₂)*p₀

= _1*p₀ + _2*p₃ – (_₁)*p₁ (2)

= _2*p₀ + _1*p₃ – (₁₂)*p₂

= _2*p₁ + _1*p₂ – (₁₊ ₂)*p₃

Чтобы решить уравнения Колмогорова и найти вероятности состояний, прежде всего надо задать начальные условия. Если мы точно знаем начальное состояние системы Si, то в начальный момент времени (при t=0) р_i(0)=1, а все остальные начальные вероятности равны 0. Так, например, уравнения (2) можно решать при начальных условиях р₀(0)=1, р₁(0)=р₂(0)=р₃(0)=0 (оба узла исправны).

Как решать подобные уравнения? Вообще говоря, линейные дифференциальные уравнения с постоянными коэффициентами можно решать аналитически, но это удобно, если число уравнений не превосходит 2, иногда –3. Если уравнений больше – их решают численными методами на ЭВМ.

Таким образом, уравнения Колмогорова дают возможность найти все вероят­ности состояний как функции времени.

Поставим вопрос: что будет происходить с вероятностями состояний при t? Будут ли р₁ и т.д. стремиться к каким-то пределам? Если эти пределы суще­ствуют и не зависят от начального состояния системы, то они называются финальными вероятностями системы. В теории случайных процессов дока­зывается, что если число состояний системы конечно, и из каждого из них можно за конечное число шагов перейти в любое другое, то финальные вероятности существуют (это условие достаточное, но не необходимое).

Предположим, что это условие выполнено, и финальные вероятности существуют: p_i(t)=p_i (i=1,2, ..n). Финальные вероятности будем обозначать теми же буквами р₁, р₂ и т.д., что и сами вероятности состояний, но разумея под ними уже не переменные величины (функции времени), а постоянные числа. Очевидно, что они тоже образуют в сумме 1:  p_i =1 (i=1,n)

Как понимать эти вероятности? При t в системе S устанавливается предельный стационарный режим, в ходе которого система случайным образом меняет свои состояния, но их вероятности уже не зависят от времени. Финальную вероятность состояния Si можно истолковать как среднее относительное время пребывания системы в этом состоянии.

Например, если система S имеет 3 состояния S1, S2, S3 и их финальные вероятности 0.2, 0.3, 0.5 соответственно, это значит, что в предельном стацио­нар­ном режиме система в среднем 2/10 времени проводит в состоянии S1, 3/10 – S2, и половину времени – в S3.

Как вычислить финальные вероятности? Если р₁, р₂ и т.д. постоянны, то их производные равны 0. Значит, чтобы найти финальные вероятности, нужно все левые части уравнений Колмогорова положить равными 0, и решить полученную систему уже не дифференциальных, а линейных алгебраических уравнений!

Можно и не писать дифференциальные уравнения Колмогорова, а прямо по графу состояний написать систему линейных алгебраических уравнений. Если перенести отрицательный член каждого уравнения из правой части в левую, то получим сразу систему уравнений, где слева стоит финальная вероятность pi, умноженная на суммарную интенсивность всех потоков, ведущих из этого состояния, а справа – сумма произведений интенсивности всех потоков, входящих в i-е состояние на вероятности состояний, из которых эти потоки исходят.

Д ля системы уравнений (7.2)

(_₂)*p₀= _1*p₁ + _2*p₂

(_₁)*p₁= _1*p₀ + _2*p₃ (7.3)

(₁₂)*p₂= _2*p₀ + _1*p₃

(₁₊ ₂)*p₃= _2*p₁ + _1*p₂

Эту систему (7.3), казалось бы, вполне можно было решить! Но эти уравнения – однородны (не имеют свободного члена, и, значит, определяют неизвестное только с точностью до произведения множителей). Необходимо воспользоваться так называемым нормировочным условием р₀+р₁+р₂+р₃=1, и с его помощью решить систему. При этом одно (любое) из уравнений можно отбросить, оно вытекает как следствие из остальных.

Зададимся численными значениями интенсивности: ₁=1, ₂=2, ₁=2, ₂=3, и решим систему (7.3). Получаем р₀=0.4, р₁=0.2, р₂=0.27, р₃=0.13, то есть в предельном стационарном режиме 40% времени система будет проводить в исправном состоянии (оба узла исправны), 20% – в состоянии ремонта первого узла, второй при этом исправен, 27% – второй ремонтируется, первый работает, и 13% времени в состоянии полной неработоспособности.

Знание этих финальных вероятностей может помочь оценить среднюю эффективность работы системы и загрузку ремонтных органов. Предположим, что система S в состоянии S0 (исправна) приносит в единицу времени доход в 8 у.е., в состоянии S1 – доход в 3у.е., в состоянии S2 – доход 5 у.е, в S3 – ничего. Тогда в предельном состоянии средний доход в единицу времени будет равен: W=0.4*8+0.20*3+0.27*5=5.15 (у.е.)

Оценим загрузку ремонтных органов, занятых ремонтом узлов 1 и 2. Узел 1 ремон­ти­руется долю времени р₀+р₃=0.33, узел 2 ремонтируется долю времени р₂+р₃=0.4.