6. Обработка и анализ результатов моделирования

Решения, принимаемые по результатам имитационного моделирования, могут быть конструктивными только при выполнении двух основных условий:

полученные результаты обладают требуемой точностью и достоверностью;

исследователь способен правильно интерпретировать полученные результаты и знает, каким образом они могут быть использованы.

Возможность выполнения первого условия закладывается, в основном, еще на этапе разработки модели и, частично, на этапе планирования эксперимента. Достоверность результатов моделирования предполагает, что модель, с помощью которой они получены, не только является «правильной», но и отвечает некоторым дополнительным требованиям, предъявляемым к имитационным моделям. Эти требования и методы оценки рассмотрим ниже.

Способность исследователя правильно интерпретировать полученные результаты и принимать на их основе важные решения существенно зависит от степени соответствия формы представленных результатов целям моделирования.

Если разработчик уверен, что полученные результаты будут использоваться в соответствии с одной четко определенной целью, форма их представления может быть определена заранее. В этом случае преобразование экспериментальных данных к требуемому виду может производиться либо в ходе эксперимента, либо сразу после его завершения. Такой подход позволяет экономить память компьютера, необходимую для хранения большого количества необработанных данных, а также сократить время на анализ результатов и принятие решения.

Если же заранее конкретизировать цель моделирования сложно или целей несколько, данные должны накапливаться в базе данных и затем уже выдаваться в требуемой форме по запросу пользователя. Как правило, по такому принципу строятся системы автоматизации моделирования.

6.1 Основная идея регрессионного анализа

Для исследования взаимосвязи между величинами Х (вход) и y (выход) используются методы корреляционного и регрессионного анализа. Результаты корреляционного анализа позволяют сделать вывод о степени зависимости между переменными, а форма зависимости уточняется методами регрессионного анализа.

На значение величины y оказывают влияние стохастические воздействия разного рода, поэтому форма связи между величинами Х и y определяется линией регрессии, показывающей, как в среднем изменяется величина y при изменении входной величины Х, т.е. приходится говорить о связи средних значений величины y c X. Эту связь характеризуют условным математическим ожиданием величины y, вычисляемым при условии, что величина Х приняла определенное значение, а аппроксимирующая функция строится как функция регрессии.

f(X, B) M[y/X]

где B - неизвестные параметры уравнения регрессии.

Задача регрессионного анализа ставится следующим образом. Для каждого i-го опыта имеется набор значений (x_i1,...,x_ik) входных параметров X₁ X_k и соответствующее им значение выходного параметра y_i. Пример опытных данных приведен в табл.6.1.

Таблица 6.1

№ опыта	Входы				Выходы Y
	X1	X2	---	Xk
1	x11	x12	---	x1k	y1
2	x21	x22	---	x2k	y2
-----	-----	-----	---	-----	-----
n	xn1	xn2	---	xnk	yn

Необходимо определить зависимость выхода y от входных факторов x_i1,...,x_ik, которая для случая линейной связи будет иметь следующий вид:

y = b₀ + b₁x₁ + b₂x₂+ ... + (6.1)

Задача сводится к определению оценок коэффициентов уравнения регрессии b₀, b₁, ... , b_k, которые с определенной степенью вероятности будут отражать влияние аргументов x_i1,..., x_ik на y.

Для определения b_k используется метод наименьших квадратов.

Таким образом, задача сводится к минимизации:

(6.2)

где y_i - фактическое (экспериментальное) значение выходной переменной,

- рассчитанное значение выходной переменной.

Можно выражение (6.2) представить с учетом (6.1):

(6.3)

То есть, процесс сводится к нахождению таких значений коэффициентов b₀, b₁, ... , b_k, которые давали бы минимальное расхождение между расчетными и измеренными значениями y.

Это условие может быть выполнено, если приравнять к нулю частные производные S по каждому из коэффициентов b₀, b₁, ... , b_k и просуммировать их по индексу i. В результате получается система обычных уравнений:

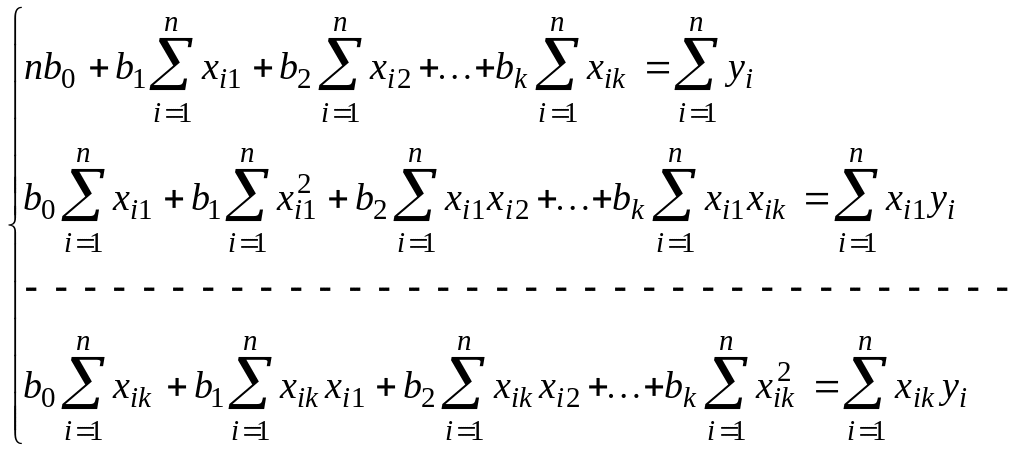(6.4)

Решая эту систему, получают коэффициенты модели (6.1) и, как следствие, явный вид уравнения регрессии для случая линейной связи.

Однако на практике часто предпочитают пользоваться несколько иной методикой определения значений коэффициентов b₀, b₁, ... , b_k уравнения регрессии, которая дает возможность определить как значения коэффициентов, ("степень" их участия в "образовании" выходной величины), так и пригодность полученного уравнения для случаев зависимости любой степени.

Если фактор может принимать значения только (+1) и (-1) – верхний и нижний уровень (дробный факторный эксперимент), то соответствующую ему переменную X называют кодированной.

Уравнения регрессии в кодированных переменных будет иметь следующий вид для случая линейной связи:

для двух переменных: y = b₀ + b₁X₁ + b₂X₂

для трех переменных: y = b₀ + b₁X₁ + b₂X₂ + b₃X₃

Необходимо отметить, что такой эксперимент дает возможность определить коэффициенты, стоящие не только непосредственно при одиночных значениях факторов в уравнении регрессии, но и коэффициенты для компонент уравнения регрессии, отражающих взаимодействие различных факторов. Однако в таком случае модель не будет являться линейной, и уравнение регрессии в кодированных переменных будет иметь следующий вид, например:

для двух переменных: y = b₀ + b₁X₁ + b₂X₂ + b₁₂X₁X₂

для трех переменных:

y=b₀+b₁X₁+b₂X₂+b₃X₃+b₁₂X₁X₂+b₁₃X₁X₃+b₂₃X₂X₃+b₁₂₃X₁X₂ X₃