Практическое занятие №4

Определение кратчайших путей по деревьям для узлов 1, 2, 3

1 Цель работы

По выданному ранее варианту сети определить кратчайшие пути по деревьям для узлов 1, 2, 3.

2 Теоретическая часть

Кратчайшим путем называется путь, имеющий минимальную длину возможного маршрута, соединяющего вершину S с вершиной t. Задача нахождения кратчайших путей с минимальным весом строится для графа G со взвешенными ребрами, т. е. на ребрах задается вес, обозначающий либо длину ребра, стоимость С, емкость β, либо количество каналов n, соединяющих два узла. Это задача решается с помощью алгоритмов ПРИМА или ДЕЙКСТРА. Этот алгоритм (ПРИМА) строится на следующих условиях:

1. задан граф G, ребра которого имеют определенный вес или длину W (i,j). Если ребра нет, то W (i,j) принимается равным ∞ (0);

2. расстояние от вершины S к вершине t должно быть минимальным и в самой вершине это расстояние берется равным нулю.

d(S,t) → min,

d(i,i) = 0.

Для маршрута S0 найти минимальный путь

, условие минимизации.

Алгоритм:

1) построить дерево Di, , которое является остовом минимального веса. Остов – это дерево с минимальным числом ребер, соединяющих узел S с узлом t;

2) выбрать ребро минимального веса и построить вершину для минимального ребра;

3) если существует следующее минимальное ребро до инцидентного узла, то построить его внутри дерева Di;

4) если i = n – 1, то есть количество ребер конечно, то остов минимального веса построен, иначе перейти к шагу 2.

3 Порядок выполнения работы

1 Построить таблицу путей.

2 Построить матрицу весов и найти кратчайшие пути по деревьям для узлов 1, 2, 3.

3 Построить деревья узлов для найденных путей.

Продолжим операции для нашего графа, где уже задан вес каждого ребра. В качестве веса ребра выбрали его длину.

Перечень путей между узлами сети записывают в виде таблицы путей А (таблица 3), состоящих из k – строк и m – столбцов. Матрица А используется при программной реализации алгоритма построения деревьев путей.

A(k*m), k – число путей; m – число ветвей в этом пути.

Элемент матрицы a_ij = 1, если ветвь β_i принадлежит пути μ_i. Если ветвь не принадлежит пути μ_i, то для простоты записи этот элемент в таблицу не вносится.

Аналогично матрицы путей строятся для путей 1–4, 1–3.

таблица 3

Матрица путей

β j	β12	β15	β23	β24	β35	β45	β25	β34
μ1(215)	1	1
μ2(235)			1		1
μ3(245)				1		1
μ4(2345)			1			1		1
μ5(2435)				1	1			1

Перейдем к пункту 2. Для расчета минимального веса надо построить матрицу весов. Матрица весов строится точно так же, как и матрица связности, но вместо 1 ставим значения веса данного ребра, а по диагонали – 0 или знак ∞.

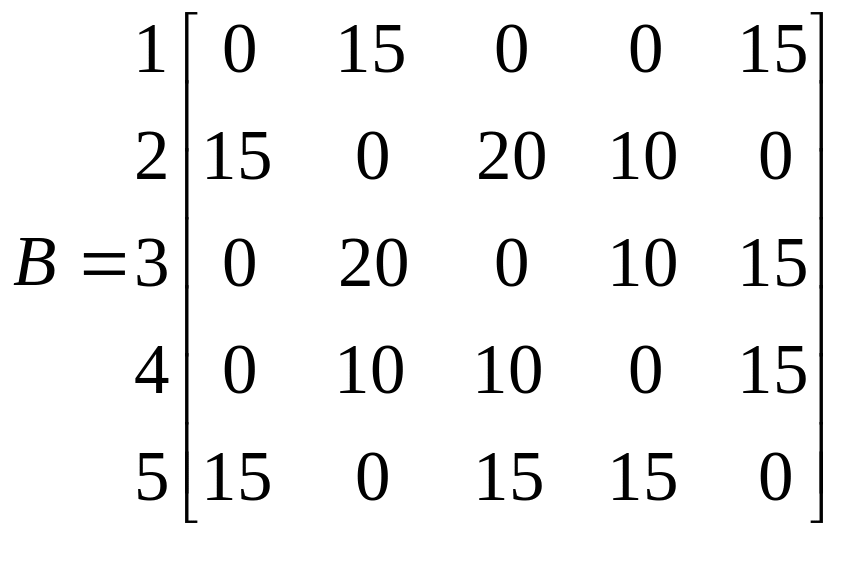
Длина полученных путей складывается из длин составляющих ребер, например: М₁₄={1, 2, 3, 4; 1, 2, 4; 1, 5, 3, 4; 1, 5, 4}

(1, 2, 4) = 15+10=25 – минимальный путь;

(1, 5, 4) =15+15 = 30;

(1, 2, 3, 4) = 15+20+10 = 45–максимальный путь;

(1, 5, 3, 4) = 15+15+10 = 40.

Дерево узлов для найденных путей 1– 4 (рисунок 8):

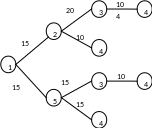
Рисунок 8.

Контрольные вопросы:

1 Как определяется матрица весов?

2 Что такое логическая структура сети?

3 Какая сеть называется неориентированной?

4 Что такое нуль-граф?

5 Какие алгоритмы нахождения кратчайших путей вы знаете?