Практическое занятие №3

Построение множества путей для узлов по выданной графовой модели сети

1 Цель работы

По выданной преподавателем каждому студенту графовой модели сети построить множество путей для узлов.

2 Теоретическая часть

Структура сети (ее топология–совокупность пунктов (узлов, станций и т.п.) и соединяющих их линий или каналов в их взаимном расположении) показывает потенциальные возможности сети обеспечивать связь между отдельными пунктами этой сети. От выбора топологии связей существенно зависят многие характеристики сети: простота присоединения новых узлов, надежность сети, сбалансированность загрузки сетевых каналов. При рассмотрении структуры сети выделяют следующие аспекты её описания: физический, определяющий состав и связи элементов и логический, отображающий взаимодей­ствие элементов в процессе функционирования сети.

Для изучения структурных свойств сетей их удобнее всего представить в виде графа без петель. Граф представляет собой математическую модель топологической структуры сети.

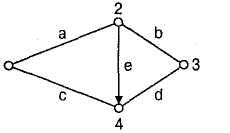
Рисунок 5. Граф структуры сети

Вершины графа (1, 2, 3, 4) сопоставляются с УК и/или ОП, а ребра графа (а, b, с, d, e) соответствуют каналам связи. В символической форме графы обозначаются – G (А, В), А = {а₁, а₂, …, a_N} – множество вершин графа; В = {b_ij} – множество ребер между вершинами a_j и a_j. Вершины графа называются смежными, если они соединены ребром. Ребра могут быть ориентированными или направленными (ребро е) и неориен­тированными или ненаправленными (ребра а, b, с, а). Ориентиро­ванные ребра соответствуют односторонним каналам, а неориенти­рованные – двухсторонним каналам.

Следовательно, графы бывают ориентированные, все ребра которых ориентированные; неориентированные графы, не содержащие ориентированных ребер; графы смежного типа, в которых имеются как ориентированные, так и неориентированные ребра.

Взвешенным называется граф, в котором вершинам и ветвям соответствуют некоторые числа, называемые весами. Каждому ребру может быть приписан некоторый «вес» – число или совокупность чисел, характеризующих какие-либо свой­ства данного ребра. В качестве веса принимаются, например, длина канала, пропускная способность, скорость передачи информации, число стандартных каналов, надежность, стоимость и т. д. Верши­нам графа также могут быть приписаны веса.

Нуль-граф (вполне не связный граф, пустой граф) – граф, не содержащий ребер.

Число входящих или исходящих (инцидентных) ребер, называют рангом узла r(a_i), где i – номер узла r(a₁) = 2, r(а₂) = 3. Узел ранга 1 является тупиковым, т. к. через него не могут про­ходить никакие пути.

Путь _ij из узла a_i в узел a_j – это упорядоченный набор ребер, начинающихся в узле a_i и заканчивающихся в узле a_j, причем конец каждого предыдущего ребра совпадает с началом последующего ребра. Путь должен быть самонепересекающимся, т. е. не проходящим дважды через один и тот же узел.

Рангом пути r (_ij) называется число ребер, входящих в данный путь. Минимальный ранг пути равен 1, например, r (₁₂) = 1, а макси­мальный – равен N – 1, где N – число вершин графа, в этом случае путь проходит через все вершины. Путь, начинающийся и заканчивающийся в одной и той же вер­шине, называется контуром (циклом).

В реальной сети, как правило, для связи между заданными узлами используются не все возможные пути, а только пути, выделенные по какому-либо показателю или обладающие некоторыми заданными свойствами.

Связной называется сеть, любые узлы которой связаны хотя бы одним путем. Связностью h называется минимальное число независимых пу­тей, между всеми парами вершин. Для графа h = 2. Понятие связности чаще относится не ко всей сети в целом, а к заданным узлам, а также к множеству путей, обладающих заданным свойством. При этом можно вводить ограничения по рангу. Например, в нашем случае h₂₄ = 3 , h₂₄(r = 1) =1.