Практическое занятие №1

Характеристики источника дискретных сообщений

1 Цель работы

Рассчитать основные характеристики источника дискретных сообщений.

2 Теоретическая часть

В основу измерения количества информации положены вероятностные характеристики передаваемых сообщений, которые не связаны с конкретным содержанием сообщений, а отражают степень их неопределенности (неожиданности).

Чем меньше вероятность сообщения, тем больше информации оно несет. Количество информации в отдельно взятом сообщении определяется величиной, обратной вероятности сообщения и вычисляется в логарифмических единицах:

При использовании десятичных логарифмов информация измеряется в дитах, для натуральных логарифмов единица измерения информации – это нат, а для систем, работающих с двоичными кодами – это бит, т. е. Бит – это количество информации, которое передается сообщением, вероятность которого равна 0,5:

Большинство реальных источников выдают сообщения с различными вероятностями, поэтому практически необходимо знать среднее количество информации, приходящееся на одно сообщение.

Это среднее количество информации называется энтропией источника сообщений и измеряется в бит/сообщение:

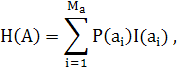
где Мa – общее число сообщений источника.

Логарифмическая мера информации предложена в 1928 г. англичанином Р. Хартли, а термин «энтропия» введен в 1948 г. американцем К. Шенноном.

Энтропия – это мера неопределенности в поведении источника сообщений (ИС). Она равна нулю, если с вероятностью равной единице источником выдается всегда одно и то же сообщение (в этом случае неопределенность в поведении ИС отсутствует). Энтропия максимальна, если сообщения выдаваемые источником появляются независимо и с одинаковой вероятностью. Энтропия всегда положительна и принимает максимальное значение при равновероятностных сообщениях.

Избыточность сообщения оценивается коэффициентом избыточности:

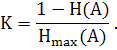
Избыточность при передаче сообщений имеет свои положительные и отрицательные стороны: увеличение избыточности приводит к увеличению времени передачи сообщений, излишней загрузке каналов связи; при этом за заданный промежуток времени по каналу передается меньшее количество информации, чем это возможно, поэтому одной из задач теории информации и техники кодирования является задача сокращения избыточности. Однако увеличение избыточности повышает помехоустойчивость передачи сообщений, так как позволяет легко исправлять отдельные ошибки или восстанавливать пропуски букв или слов в сообщении.

При практическом выполнении систем связи устанавливается компромиссное значение избыточности, обеспечивающее заданные скорость и надежность передачи сообщений.

Непрерывное сообщение в общем случае принимает бесконечное число значений, как по времени, так и по уровню, поэтому количество информации и, соответственно, энтропия источника непрерывного сообщения бесконечны. В реальных условиях отсчеты сообщений по времени производятся в дискретных точках через интервал дискретизации согласно теореме Котельникова, т. е. с заданной степенью точности непрерывное сообщение можно представить конечным числом значений по уровню, тогда среднее значение количества информации в одном отсчете (энтропия отсчета) можно вычислить аналогично дискретным сообщениям:

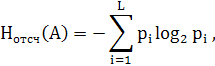
где pi – вероятность появления в квантованном сообщении i –того уровня;

L – конечное число значений по уровню.

Под производительностью источника понимают среднее количество информации, создаваемой источником в единицу времени:

где А – сообщение;

tср – средняя длительность сообщения.

Для непрерывных сообщений при их преобразовании в цифровую форму с частотой дискретизации и при числе равновероятностных уровней квантования L (вероятность каждого уровня pi = 1/L), значение производительности источника непрерывных сообщений равно:

Бит в секунду, бит/с (англ. bits per second, bps) — базовая единица измерения скорости при последовательной передаче данных.

Бод (англ. baud) в связи и электронике — единица измерения символьной скорости, количество изменений информационного параметра несущего периодического сигнала в секунду. Названа по имени Эмиля Бодо, изобретателя кода Бодо — кодировки символов для телетайпов.

Зачастую, ошибочно, считают, что бод — это количество бит, переданное в секунду. В действительности же это верно лишь для двоичного кодирования, которое используется не всегда. Например, в современных модемах используется квадратурная амплитудная манипуляция, и одним изменением уровня сигнала может кодироваться несколько (до 16) бит информации. Например, при символьной скорости 2400 бод скорость передачи может составлять 9600 бит/c благодаря тому, что в каждом временном интервале передаётся 4 бита. Кроме этого, бодами выражают полную ёмкость канала, включая служебные символы (биты), если они есть. Эффективная же скорость канала выражается другими единицами, например, битами в секунду (бит/c, bps).