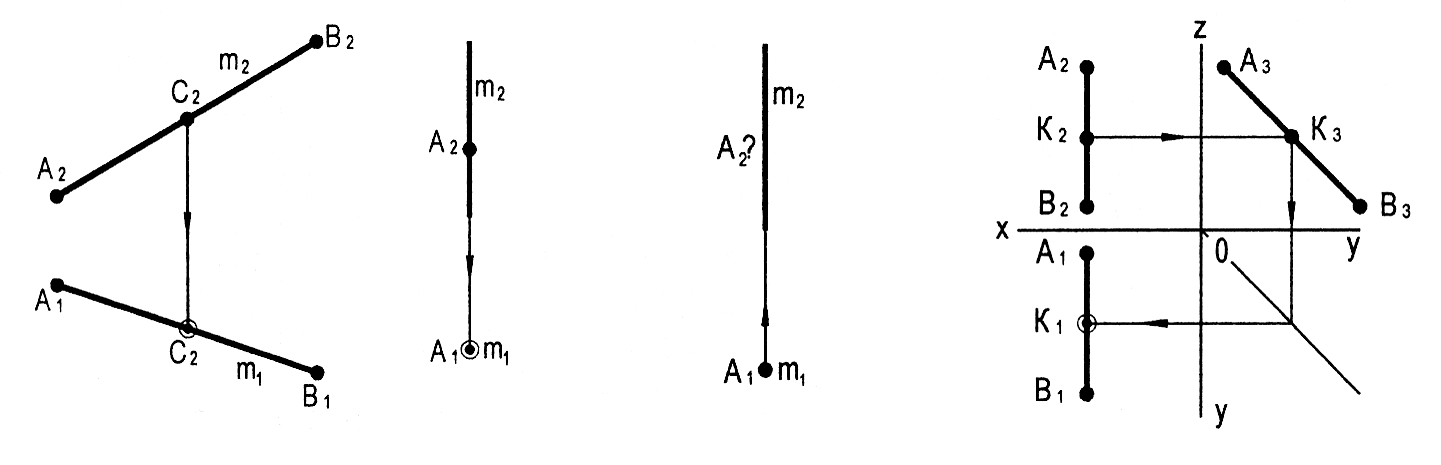Точка на прямій. Взаємне положення точки і прямої. Поділ відрізка у заданому відношенні
Якщо точка лежить на прямій, то її проекції лежать на однойменних проекціях цієї прямої і на спільній лінії зв’язку.
Точка А (рис. 2.8) лежить на прямій m, тому що її проекції А1 і А2 розташовані відповідно на горизонтальній m1 і фронтальній m2 проекціях прямої.
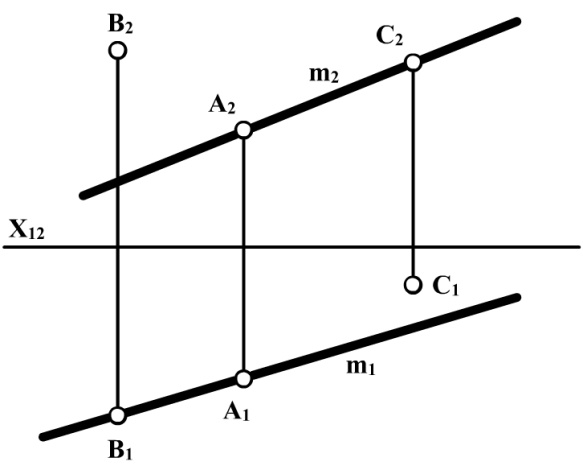
Рис. 2.8
Точки В і С не лежать на прямій m, тому що одна з проекцій кожної точки не належить проекції цієї прямої.
Точка, яка не лежить на прямій відносно прямої може займати різне положення. Наприклад: точка В знаходиться над прямою m, а точка С – за прямою m. Для визначення належності точки профільній прямій, необхідно побудувати профільні проекції точки та прямої.
Побудова відсутніх проекцій точок на прамій в окремих випадках вирішується просто, в інших випадках рішення неможливе, в третіх – рішення громіздке (табл. 2.1).
Таблиця 2.1
Належність точки прямій
Просто |
Неможливо |
Громіздко |
|
|
|
Розглянемо поділ відрізка АВ у заданному відношенні, наприклад 3:2. Згадаємо одну з властивостей паралельних проекцій: якщо точка ділить відрізок у даному відношенні, то проекція точки ділить проекцію відрізка у такому ж відношенні.
Щоб поділити відрізок АВ точкою С у відношенні 3:2 досить поділити одну його проекцію у даному відношенні (наприклад А1В1) відомим з геометрії способом. З точки А1 проводимо довільний промінь, на якому від точки А1 відкладаємо п’ять однакових довільних відрізків. Кінець п’ятого відрізка (точку 5) з'єднуємо з точкою В1. Кінець другого відрізка позначаємо 3. Точка 3 ділить відрізок А15 у відношенні 3:2.
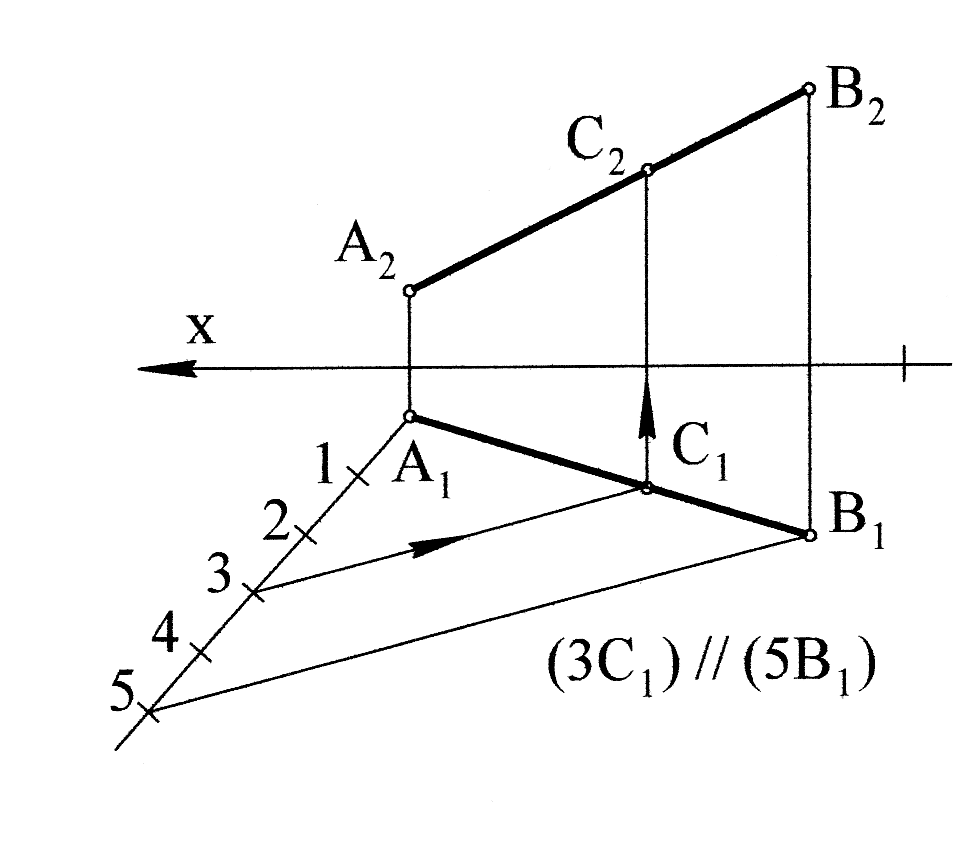
Рис. 2.9
Через точку 3 проводимо пряму, яка паралельна відрізку 5В1. Ця лінія перетинає горизонтальну проекцію відрізка АВ в точці С1. С1 ділить А1В1 у відношенні 3:2. За допомогою лінії зв’язку знаходимо відсутню фронтальну проекцію точки С на А2В2 (рис. 2.9).
Сліди прямої
Пряма загального положення перетинає всі основні площини проекцій.
Якщо відрізок АВ загального положення продовжити в обидва боки від точок А і В, то в точках М і N він перетне площини проекцій П1 і П2 (рис. 2.10).
Точки перетину прямої з площинами проекцій називаються слідами прямої. Точка М – горизонтальний слід прямої АВ, а точка N – фронтальний.
Слід – це точка, яка одночасно належить прямій і площині проекцій. З цієї умови витікає правило побудови слідів прямої. Побудувати сліди прямої на комплексному кресленні означає –знайти проекції слідів.
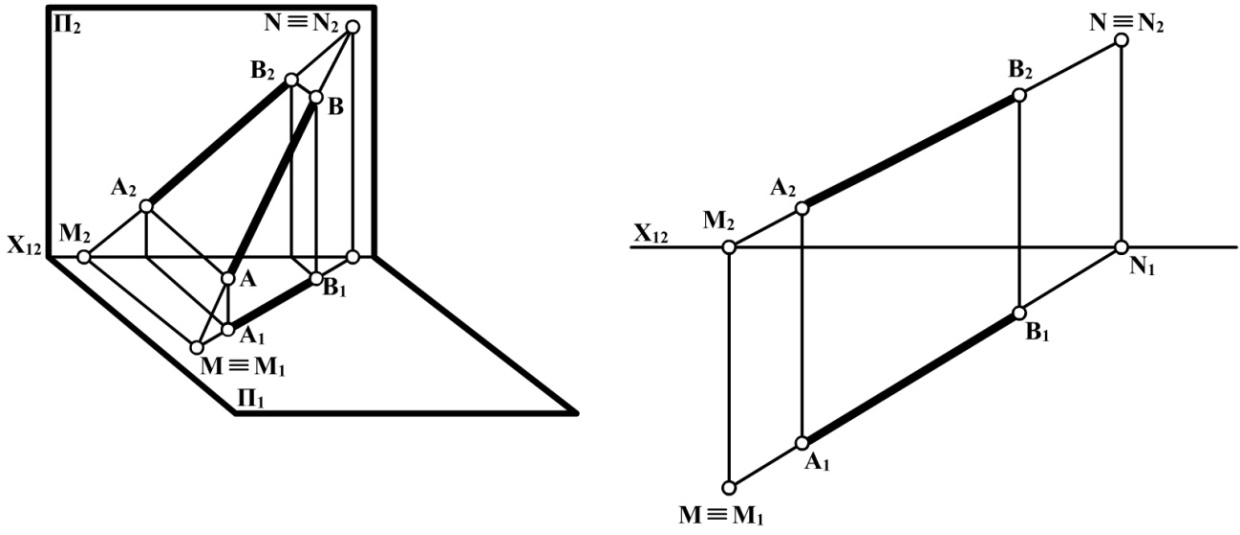
Рис. 2.10
Горизонтальний слід прямої – це точка, яка належить прямій, а тому її проекції належать проекціям прямої. З іншого боку ця точка належить і площині проекцій П1, тому вона має особливості точок, які належать площинам проекцій: одна координата дорівнює нулю. Для точки, яка лежить на П1 – Z = 0. Точка прямої АВ, для якої Z = 0, на комплексному кресленні (рис. 2.10) знаходиться на перетині фронтальної проекції прямої АВ (А2В2) з віссю Х12. Це точка М2 – фронтальна проекція горизонтального сліду прямої. Точка М1 знаходиться на одній вертикальній лінії зв'язку з М2 і належить горизонтальній проекції прямої.
Таким чином, для побудови на комплексному кресленні горизонтального сліду М прямої АВ необхідно:
1) Продовжити фронтальну проекцію А2В2 до перетину з віссю Х12 в точці М2. Точка М2 – фронтальна проекція сліду М.
2) Провести через точку М2 вертикальну лінію зв’язку до перетину з горизонтальною проекцією А1В1 прямої (або її продовженням) в точці М1 (горизонтальній проекції сліду), яка збігається з самим слідом М.
Фронтальний слід прямої – це точка, яка належить прямій, а тому її проекції належать проекціям прямої. З іншого боку ця точка належить і площині проекцій П2, тому вона має особливості точок, які належать площинам проекцій: одна координата дорівнює нулю. Для точки, яка лежить на П2 – Y = 0. Точка прямої АВ, для якої Y = 0, на комплексному кресленні (рис. 2.11) знаходиться на перетині горизонтальної проекції прямої АВ (А1В1) з віссю Х12. Це N1 – горизонтальна проекція фронтального сліду прямої. N2 знаходиться на одній вертикальній лінії зв'язку з N1 і належить фронтальній проекції прямої.
Рис. 2.11
Таким чином, для побудови фронтального сліду (точки N) прямої АВ необхідно:
1). Продовжити горизонтальну проекцію А1В1 до перетину з віссю Х12 в точці N1. Точка N1– горизонтальна проекція сліду N.
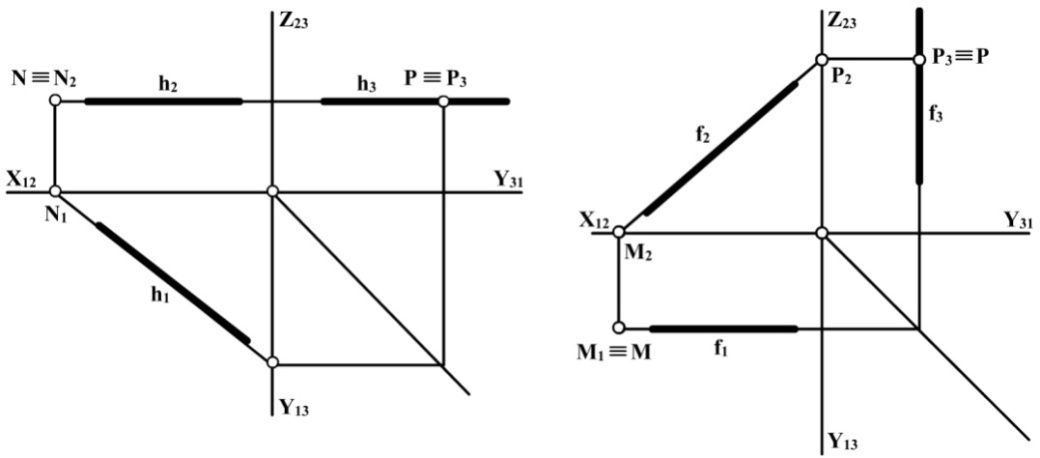
Рис. 2.12
2). Провести через точку N1 вертикальну лінію зв’язку до перетину з фронтальною проекцією А2В2 прямої (або її продовженням). Отримаємо точку N2 (фронтальну проекцію сліду) яка збігається з самим слідом N (рис. 2.11).
Пряма загального положення в системі трьох площин проекцій має три сліди: горизонтальний, фронтальний і профільний; пряма рівня – два сліди; проеціююча пряма – один слід. На рисунку 2.12 показана побудова фронтального сліду N і профільного сліду Р горизонталі h, а також горизонтального сліду М і профільного сліду Р фронталі f.
Горизонтально-проеціююча пряма а має один горизонтальний слід М (М1), який збігається з горизонтальною проекцією прямої а (рис. 2.13).
Фронтально-проеціююча пряма b має один фронтальний слід N(N2), який збігається з фронтальною проекцією прямої b (рис. 2.14).
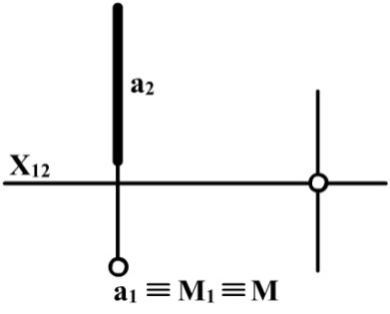
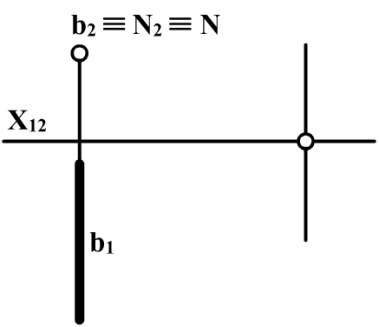
Рис. 2.13 Рис.2.14