Ортогональні проекції і система прямокутних координат
У просторі є безліч точок, що займають різне положення щодо площин проекцій П1, П2 і П3. У такому разі положення точки визначають дійсними величинами. Для цього в системі площин проекцій П1, П2, П3 розміщується така ж система прямокутних декартових координат. Початок координатних осей суміщається з початком осей проекцій. Тепер положення кожної точки визначають трьома координатами – висотою, глибиною і широтою, які показують величини відстаней, на які точка віддалена від площин проекцій.
Висота точки (Z) визначає її відстань від площини проекцій П1 – А А1 (на комплексному кресленні це відрізок А12А2 ).
Глибина точки (Y) визначає її відстань від площини проекцій П2 – А А2 (на комплексному кресленні це відрізок А12А1)
Широта точки (Х) визначає її відстань від площини проекцій П3 – А А3 (на комплексному кресленні це відрізок А12О123).
Між координатами точки та її ортогональними проекціями існує зв’язок:
1) координата Х визначає положення вертикальної лінії зв’язку;
2) координата Y визначає положення горизонтальної проекції точки;
3) координата Z визначає положення фронтальної проекції точки.
Конкуруючі точки
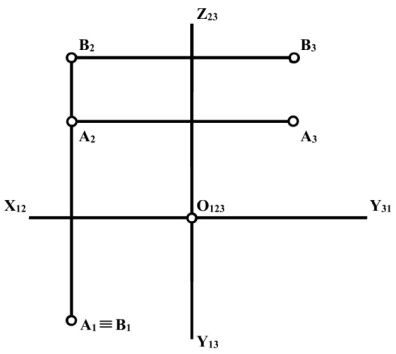
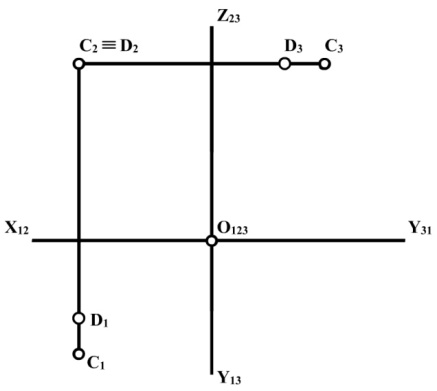
Точки, проекції яких хоча б на одну із площин проекцій співпадають (точки, які лежать на одному проеціюючому промені) називають конкуруючими. Так, точка А знаходиться над точкою В (рис. 1.13), а точка D знаходиться перед точкою С (рис. 1.14).
Конкуруючі точки застосовують під час визначення видимості непрозорих фігур.
Правило конкуруючих точок:
- з двох конкуруючих точок у горизонтальній проекції видима та, висота якої більша;
- з двох конкуруючих точок у фронтальній проекції видима та, глибина якої більша;
- з двох конкуруючих точок у профільній проекції видима та, широта якої більша.
.
Рис. 1.13 Рис. 1.14
Точка в квадрантах і октантах простору
П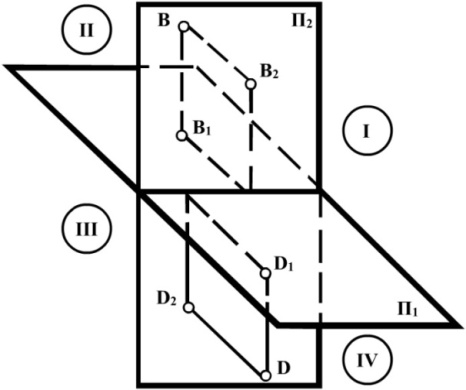
лощини
проекцій П1
і
П2
ділять простір на чотири двогранні
кути, які називають квадрантами.
Наприклад,
точка
В
–
ІІ
квадрант; точка
D – ІV квадрант
(рис.
1.15).
Рис. 1.15
Площини П1, П2, П3 ділять простір на вісім у геометричному відношенні одинакових частин – октантів (рис. 1.16).
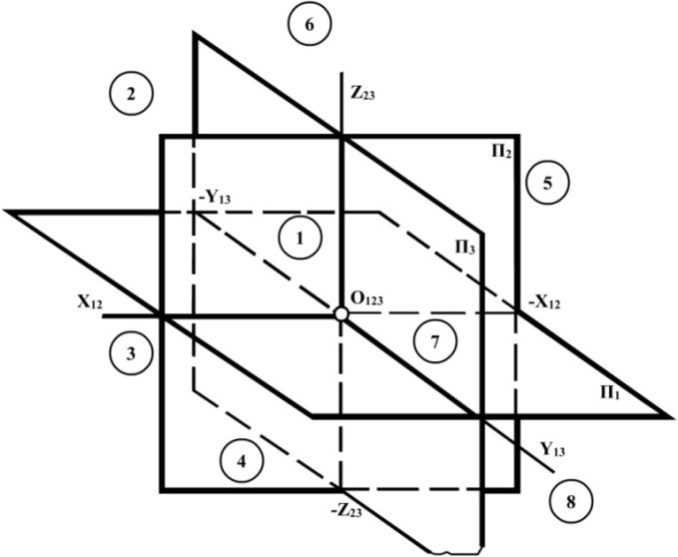
Рис. 1.16
Знаки координат точок за октантами подано в таблиці:
-
Окт.
X
Y
Z
Окт.
X
Y
Z
I
+
+
+
V
-
+
+
II
+
-
+
VI
-
-
+
III
+
-
-
VII
-
-
-
IV
+
+
-
VIII
-
-
+
На рис 1.17 наведено комплексне креслення в системі площин (П1П2П3) точок А(3; 4; 2) і В (2; 3; -2), С (-1; 0; 3). Одиницю виміру позначено штрихом на координатних осях. Точка А знаходиться в першому октанті, точка В – у четвертому октанті, точка С належить площині П2. Слід відмітити, що точка С одночасно належить п’ятому та шостому октантам.
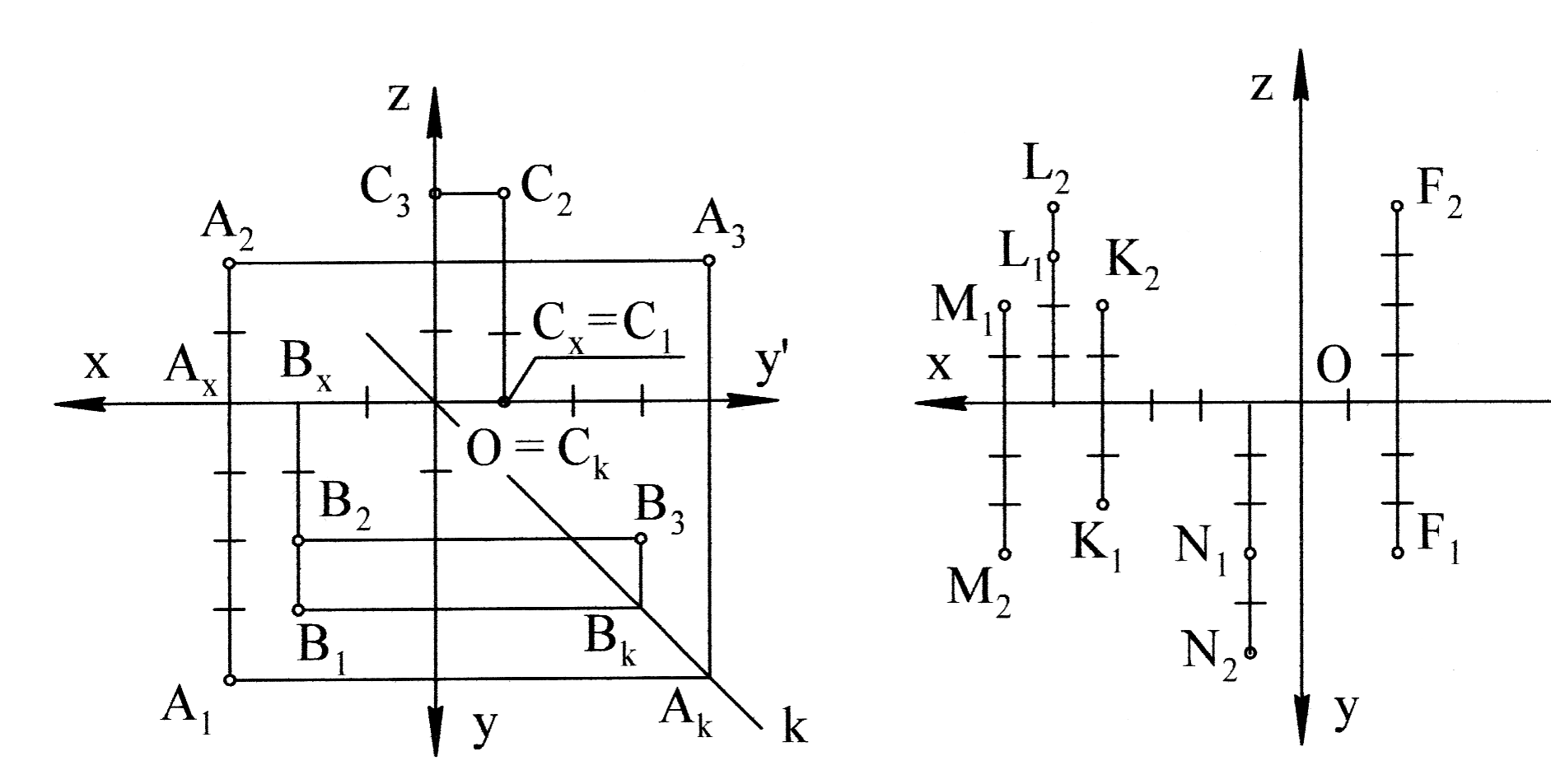
Рис. 1.17 Рис. 1.18
На рис. 1.18 наведено комплексне креслення в системі площин (П1П2) точок К (4; 2; 2), L (5; - 3; 4), М (6; -2; -3), N (1; 3; -5) і F (-2; 3; 4). Точки К і F належать першій квадранті, точка L – другій, точка М – третій, точка N – у четвертій квадранті.
Надалі розглядаючи комплексне креслення фігур у системі площин (П1П2) приймається одиниця виміру – один міліметр і спеціально позначати штрихами не будемо.
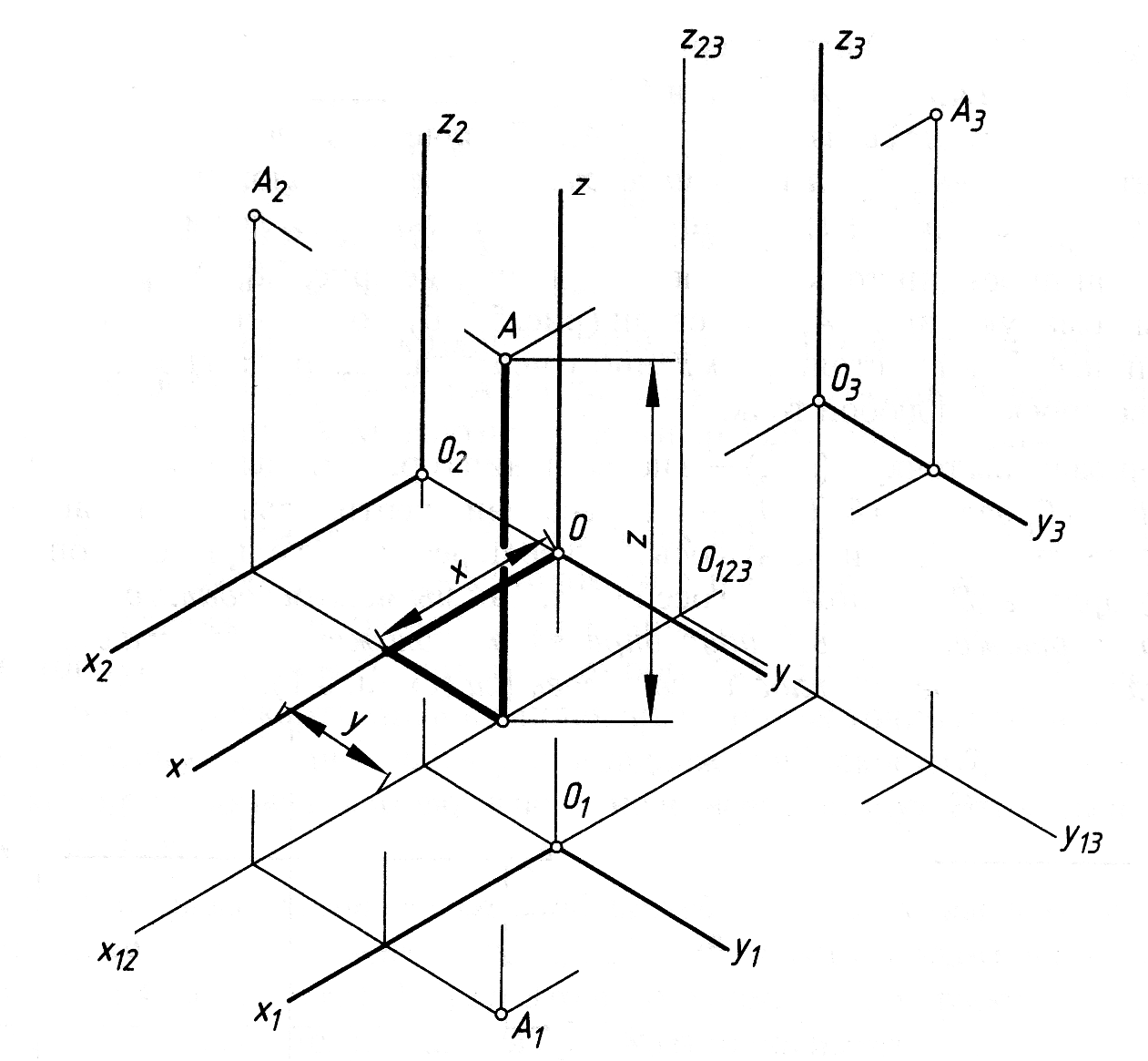
Рис. 1.19
Креслення виробу обов’язково супроводжується параметризацією і нанесенням розмірів, за якими виготовляють виріб. При цьому система відліку, яку будемо називати натуральною системою координат, не співпадає із проекційною системою, проте її вибирають так, щоб її осі були відповідно паралельні осям проекцій (рис. 1.19).
Рис. 1.20
Натуральна система Охуz разом із об’єктом (точка А) спроеціюється на площину проекцій. При цьому її координатні площини паралельні площинам проекцій і їх поля перспективно відповідним. Для задання такої моделі на епюрі достатньо задати початок 0 (01 02 03) натуральної системи Охуz (рис. 1.20). Тоді зображення А1, А2, А3 об’єкту А можна побудувати за координатами А (хуz) натуральної системи.