Двокартинне комплексне креслення точки

Точка – це геометричний образ, який не має вимірів. Уся термінологія в нарисній геометрії з винятковою наочністю свідчить про те, що поняття про геометричні образи виникли внаслідок абстрагування від реальних предметів різної форми. Так, наприклад, слово точка походить від дієслова «ткнути» і означає результат миттєвого дотикання, уколу.

Проекція точки – точка. Але за однією проекцією точки А не можна однозначно визначити положення в просторі точки – оригіналу (А) бо всі точки В, С, D,..., що належать проеціюючій прямій (SА) проеціюються у точку А₁ (рис. 1.6). Тобто, рисунок точки є незворотнім.

С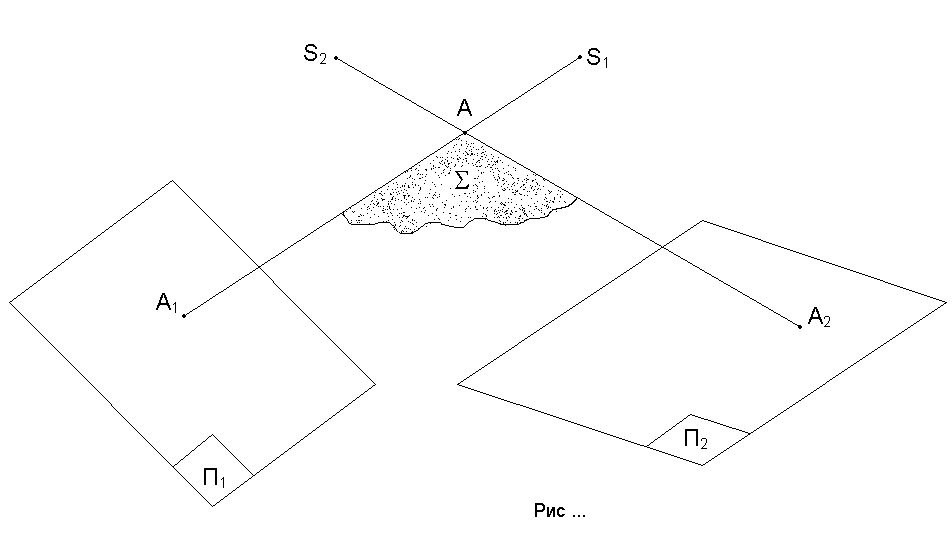 проеціюємо точку А на дві площини проекцій П₁ та П₂ (рис. 1.7) із двох центрів S₁ та S₂. Прямі S₁А та S₂А задають проеціюючу площину  ((S₁АS₂А)). Покажемо, що проекції А₁ та А₂ однозначно визначають точку А. Дійсно, проеціюючі прямі S₁А та S₂А, як такі, що належать площині  перетинаються в єдиній точці А.

Рис. 1.6 Рис. 1.7

Отже, для того щоб рисунок точки був зворотнім, необхідно мати проекції її, як мінімум, на дві непаралельні площини.

Французький інженер-математик Гаспар Монж уперше запропонував здійснювати проеціювання предметів на дві взаємно перпендикулярні площини. Проеціювання при цьому залишається прямокутним (рис. 1.8).

Рис. 1.8

Оскільки П₁П₂, а проеціюючі промені SП₁ і МП₂, то лінія яка з’єднує проекції точки АА₁А₂ перпендикулярна осі проекцій Х₁₂. А₂А₁₂Х₁₂; А₁А₁₂Х₁₂.

П₁ – горизонтальна площина проекцій; П₂ – фронтальна площина проекцій; Х₁₂ – вісь проекцій – лінія перетину площин П₁ і П₂; А₁–горизонтальна проекція точки А; А₂ – фронтальна проекція точки А. Лінію А₁А₂ (лінія, яка з’єднує горизонтальну і фронтальну проекції точки А) називають вертикальною лінією зв’язку.

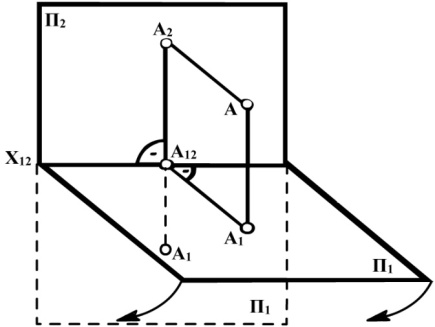
Рис. 1.9

Якщо обернути площину проекцій П₁ навколо осі Х₁₂ на кут 90⁰ до суміщення її з площиною проекцій П₂ (рис. 1.9), отримаємо плоске креслення, в якому проекції точки А₁ і А₂ розташовані на одному перпендикулярі до осі Х₁₂. Цей перпендикуляр називають вертикальною лінією зв’язку. Одержане креслення отримало назву епюр Монжа. При цьому відрізок А₂А₁₂ визначає відстань від точки А до площини П₁, а відрізок А₁А₁₂ визначає відстань від точки А до площини П₂.

Для простоти побудов надалі комплексне креслення точки в системі двох площин проекцій будемо зображати так, як показано на рис. 1.10.

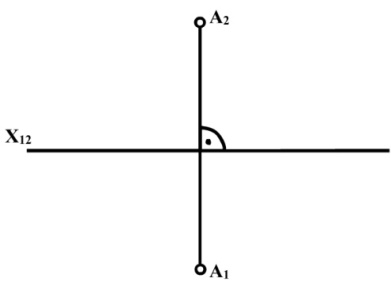
Рис. 1.10

Проекції точки на три площини проекцій

Для розв'язання окремих задач необхідно вводити в систему двох взаємно перпендикулярних площин проекцій інші площини проекцій. Розглянемо введення в систему площин П₁ і П₂ третьої площини П₃, яка перпендикулярна до заданих площин П₁ і П₂. Ця площина називається профільною площиною проекцій.

Проаналізуємо ортогональне проеціювання точки А на три взаємо-перпендикулярні площини П₁, П₂, П₃ (рис. 1.11):

П₁ –горизонтальна площина проекцій; П₂ – фронтальна площина проекцій;

П₃ – профільна площина проекцій; О – початок координат;

ОХ, ОY, OZ – осі проекцій; А₁, А₂ , А₃ – відповідно горизонтальна, фронтальна та профільна проекції точки А.

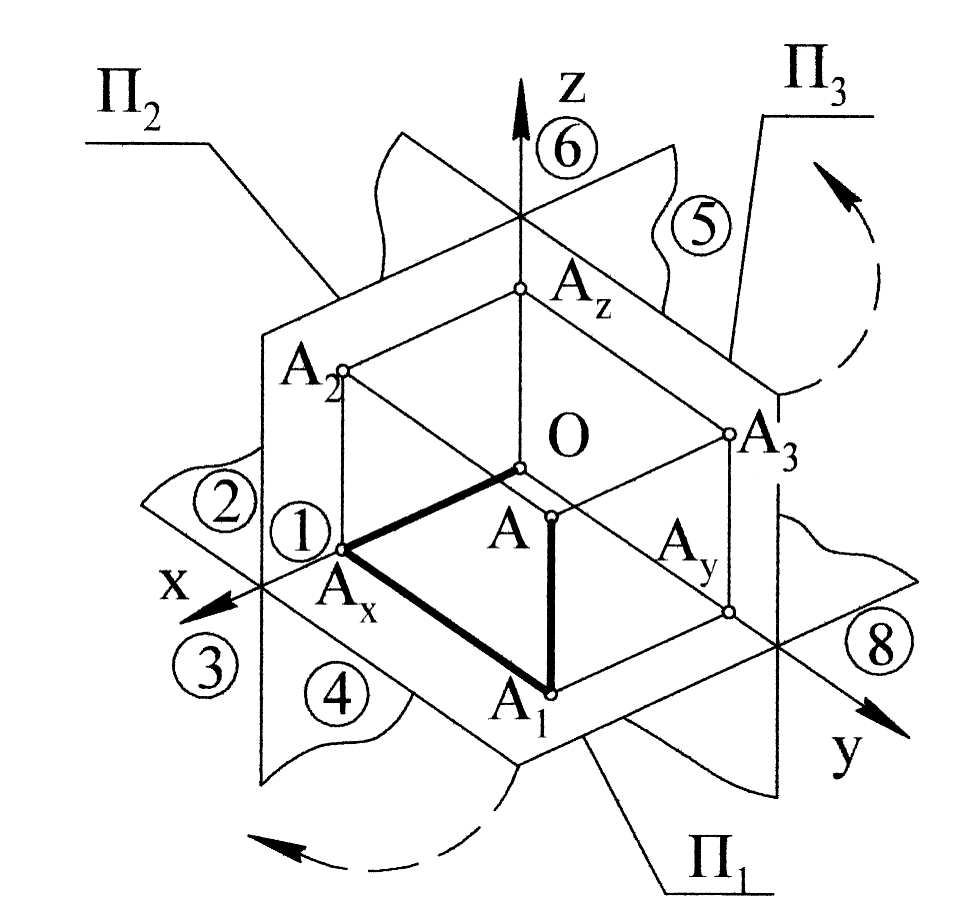
Рис. 1.11

Плоске комплексне креслення утворюється шляхом суміщення площин П₁ і П₃ з П₂. Для суміщення П₁ з П₂ необхідно повернути її на 90° навколо осі Х в напрямку руху годинникової стрілки; П₃ необхідно повернути навколо осі Z на 90° у напрямку, протилежному руху годинникової стрілки (рис. 1.12). Пряму, яка сполучає А₂ і А₃ називають горизонтальною лінією зв’язку.

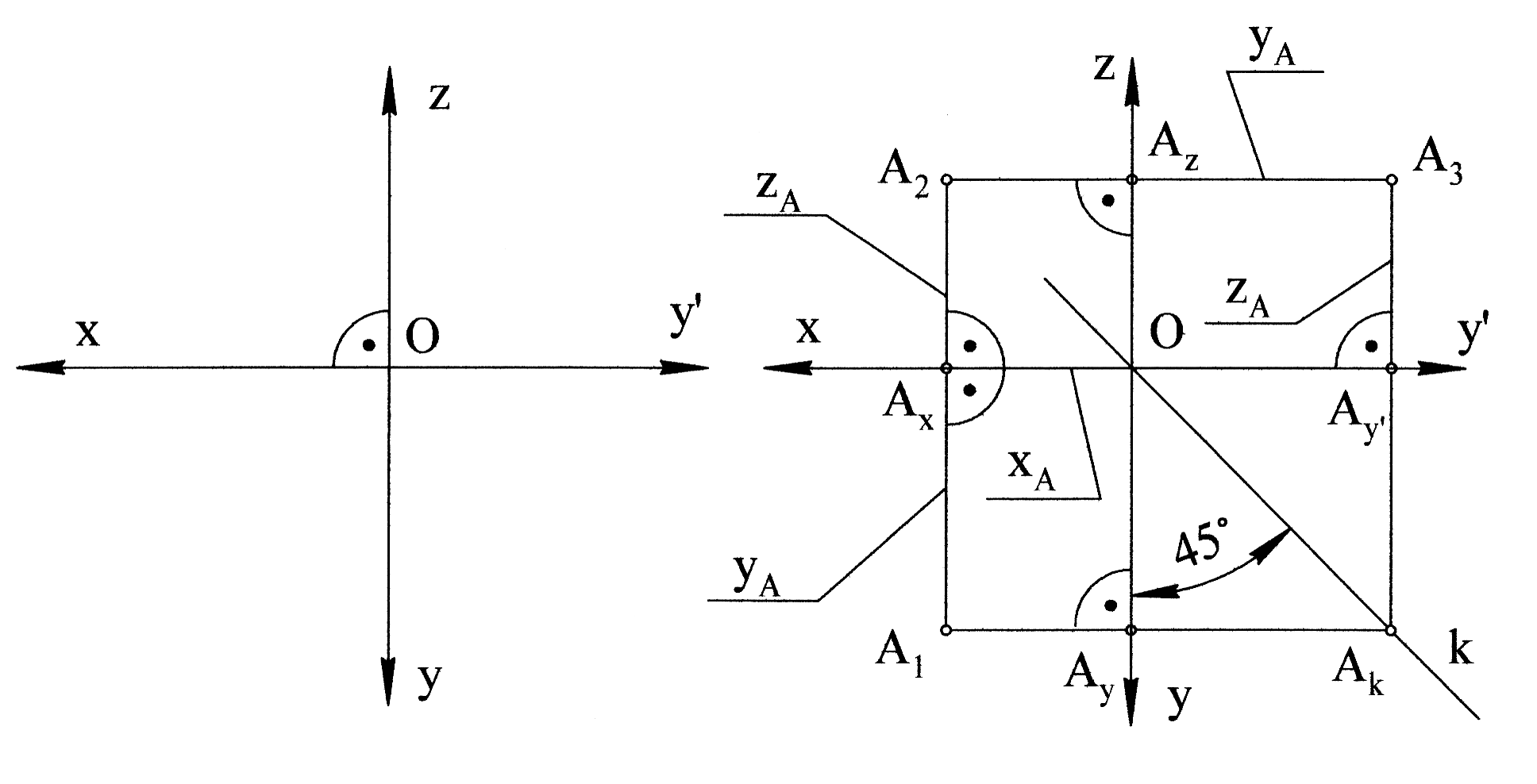
Рис. 1.12

Проекції однієї і тієї ж точки на комплексному кресленні розташовуються не довільно, а знаходяться в проекційному зв’язку (рис. 1.12), який передбачає таке:

1. Фронтальна і горизонтальна проекції точки завжди знаходяться на одній вертикальній лінії зв’язку (А₂А₁OX).

2. Фронтальна і профільна проекції точки завжди знаходяться на одній горизонтальній лінії зв’язку (A₂A₃OZ).

3. Відстань профільної проекції точки від осі OZ дорівнює відстані горизонтальної проекції від осі ОХ (|А₁А₁₂| = |А₃ А₂₃|).

Існує 3 способи отримання третьої проекції точки:

1. Проекційний, коли ніжку циркуля встановлюють у початок координат О, і розхилом циркуля, рівним координатою проводиться дуга до перетину з віссю ох.

2. За допомогою постійної креслення k проводять пряму під кутом 45⁰.

3. Координатний (найточніший і тому кращий), коли на лінії зв'язку А₂ – А₃ від осі Z відкладають координату Y.