Спосіб плоско-паралельного переміщення

На відміну від способу заміни площин проекцій, де задана фігура залишалась нерухомою, а площини проекцій змінювали своє положення, можна досягти того ж самого результату зворотним шляхом: залишаючи площини проекцій нерухомими, переміщувати фігуру в просторі як тверду систему до бажаного положення.

Плоско-паралельним переміщенням фігури в просторі називається таке переміщення, при якому усі точки фігури переміщуються в площинах, паралельних між собою і паралельних до площини проекцій.

Так, у плоско-паралельному переміщенні відносно П₁ усі точки фігури переміщуються в горизонтальних площинах рівня.

Теорема. Якщо фігура здійснює плоско-паралельне переміщення щодо П₁, то фронтальні проекції її точок будуть рухатися по прямих, перпендикулярних до ліній зв'язку. У цей час горизонтальна проекція фігури рухається по площині проекцій, залишаючись рівною самій собі.

У випадку плоско-паралельного переміщення фігури щодо П₂ горизонтальні проекції її точок рухаються по прямих, перпендикулярних до ліній зв'язку, а фронтальна проекція фігури переміщується по площині проекцій, залишаючись рівною самій собі.

Приклад 1. Перетворити пряму загального положення в проеціюючу пряму.

Спочатку перетворимо комплексне креслення так, щоб відрізок АВ став паралельним П₂, а потім так, щоб він був перпендикулярним до площини П₁ (рис. 4.9).

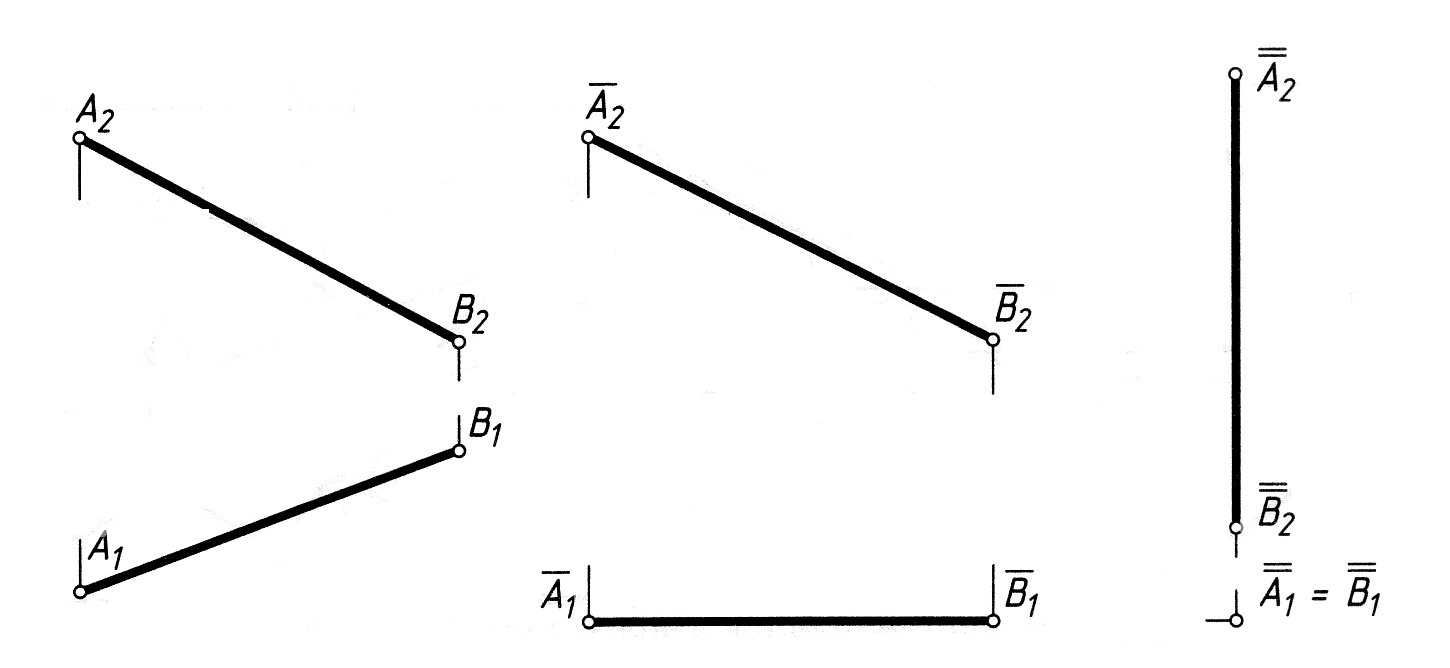
Рис. 4.9

Алгоритм розв’язку:

1. А₁В₁ = А₁В₁, А₁В₁ || X₁₂;

2. А₂В₂ = А₂В₂, А₂В₂  Х₁₂.

Приклад 2. Визначити натуральну величину АВС. АВС – площина загального положення (рис. 4.10).

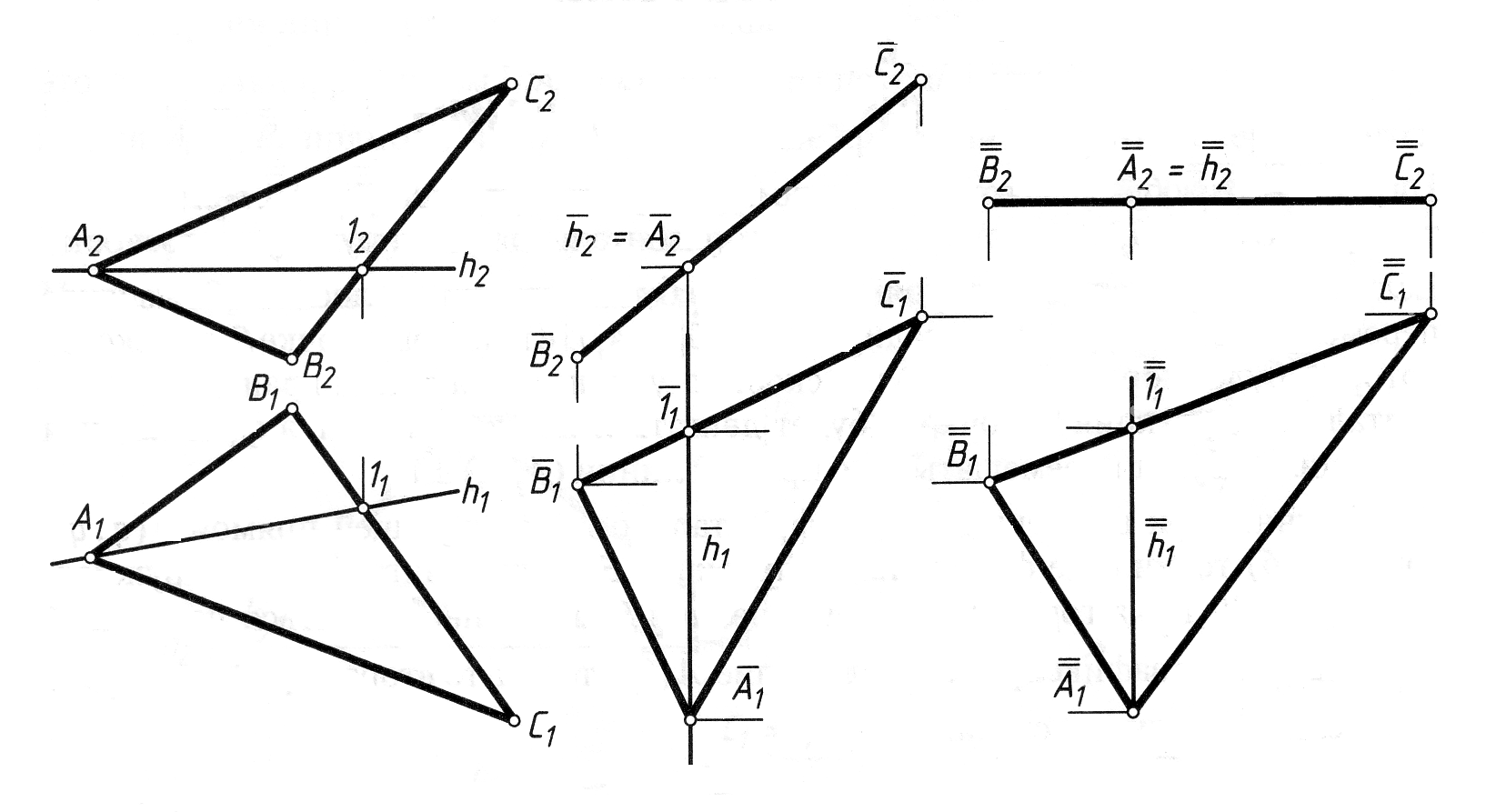
Рис. 4.10

Перетворення проводимо в два етапи:

1) Перетворюємо площину загального положення в проеціюючу. Для цього в площині проводимо лінію рівня – h або f. Розміщуємо ту проекцію площини, в якій лінія рівня є натуральною величиною так, щоб натуральна величина лінії рівня стала перпендикулярною до осі проекцій Х₁₂. При цьому лінія рівня стане проеціюючою прямою і на другу площину проекцій спроеціюється в точку. Площина при цьому стане проеціюючою щодо цієї ж площини проекцій.

2) Перетворюємо проеціюючу площину в площину рівня. Для цього ту проекцію площини, яка являє собою пряму лінію розташовуємо паралельно осі Х₁₂. Інша проекція буде відображати натуральну величину АВС.

Спосіб обертання Спосіб обертання навколо проеціюючої прямої

Частковим випадком плоско-паралельного переміщення є обертання фігури навколо осі, перпендикулярної до однієї з площин проекцій. При цьому всі точки фігури рухаються (переміщуються) по колах у площинах рівня, перпендикулярних до осі обертання. Центри кіл знаходяться в точках перетину осі із вказаними площинами. Якщо точка фігури знаходиться на осі обертання, то при обертанні системи ця точка вважається нерухомою.

Таким чином, при обертанні навколо горизонтально-проеціюючої осі, фронтальні проекції точок фігури переміщуються по прямих, перпендикулярних до ліній зв'язку, а горизонтальні – по дугах кіл (рис. 4.11, а).

Під час обертання навколо фронтально-проеціюючої прямої горизонтальні проекції точок переміщуються по прямих, перпендикулярних до ліній зв'язку, а фронтальні – по дугах кіл (рис. 4.11, б).

Розв'язуючи задачі способами обертання, треба вміти показувати на кресленні такі основні елементи обертання:

1) Вісь обертання ί – пряму, навколо якої обертається точка. Вісь обертання (ί) беруть перпендикулярною до площин проекцій П₁ або П₂.

2) Площину обертання , тобто площину, в якій переміщується точка і яка перпендикулярна до осі обертання ί.

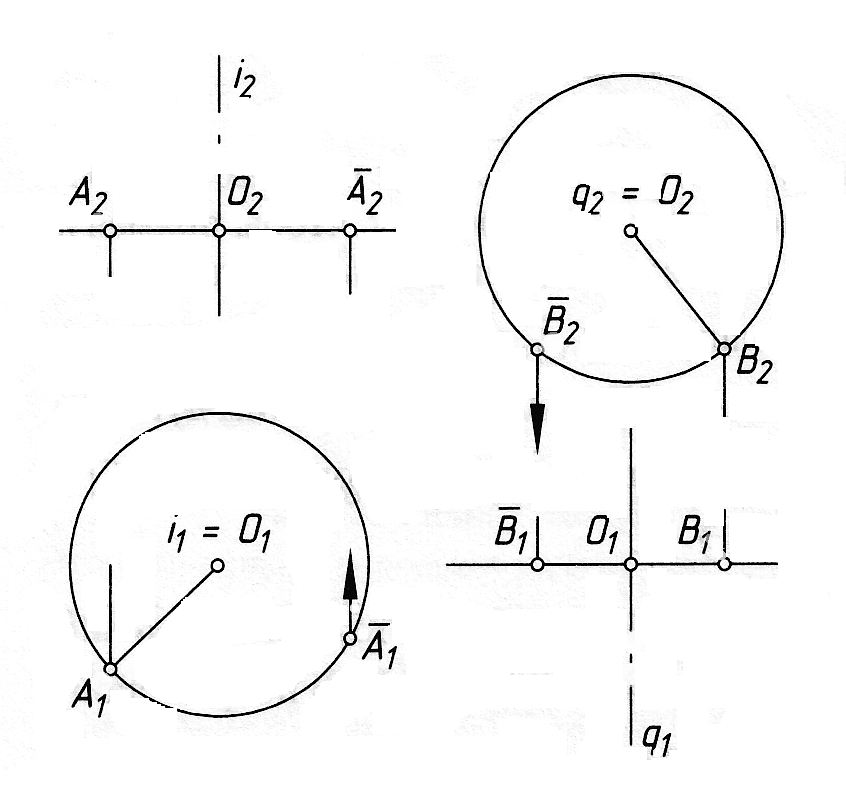
а б

Рис. 4.11

Якщо вісь обертання перпендикулярна П₁, то площина обертання буде горизонтальною. Якщо вісь обертання перпендикулярна П₂, то площина обертання буде фронтальною.

3) Центр обертання – точка О перетину осі з площиною обертання О =   ί.

4) Радіус обертання R_об. – відстань точки від центра обертання. Радіус обертання проеціюється в натуральну величину на ту площину проекцій, перпендикулярно до якої вибрано вісь обертання.

Приклад 1. Перетворити пряму загального положення в проеціюючу пряму, визначити натуральну величину її відрізка АВ (рис. 4.12).

Під час обертання прямої навколо осі доводиться обертати дві її точки. Побудова спрощується, якщо вісь обертання провести через одну з кінцевих точок відрізка: вісь ί проводимо через точку В q  П₂. Щоб визначити натуральну величину відрізка АВ, обертаємо його фронтальну проекцію до положення паралельного Х₁₂. Таким чином відрізок АВ став горизонталлю, а горизонтальна проекція В₁А₁ є його натуральною величиною. Для перетворення відрізка в проеціююче положення здійснюємо обертання відрізка АВ навколо горизонтально-проеціюючої осі ί (ί  П₁). Обертаємо горизонтальну проекцію до положення А₁В₁  Х₁₂. Фронтальна проекція відрізка стане точкою: А ₂  В₂.

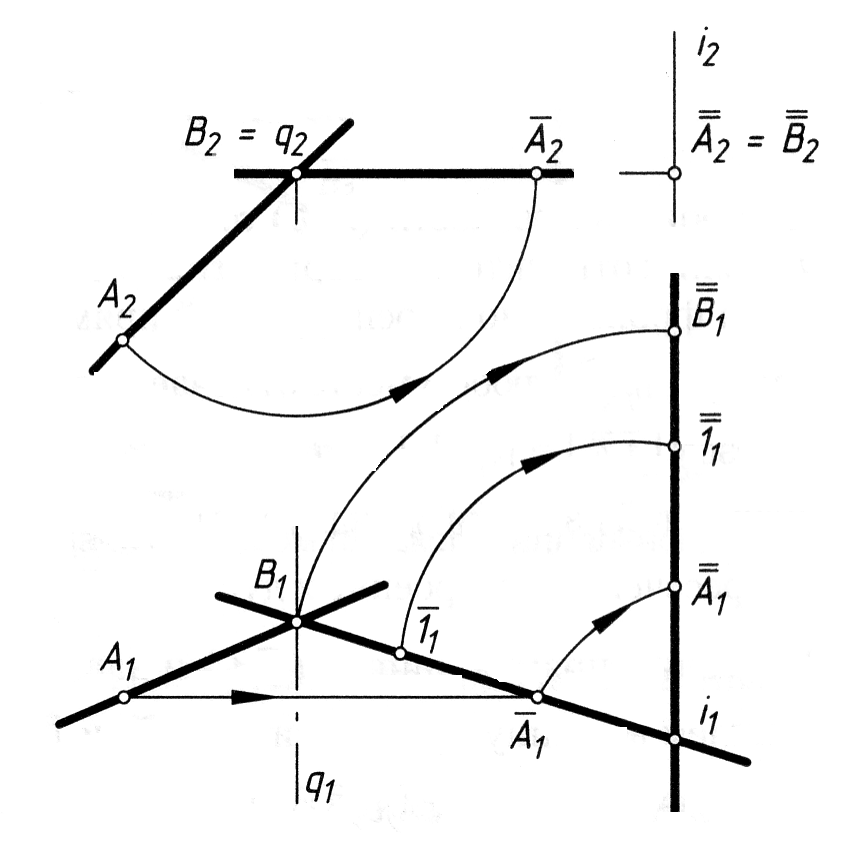
Рис. 4.12

Приклад 2. Визначити натуральну величину АВС. АВС – площина загального положення (рис. 4.13).

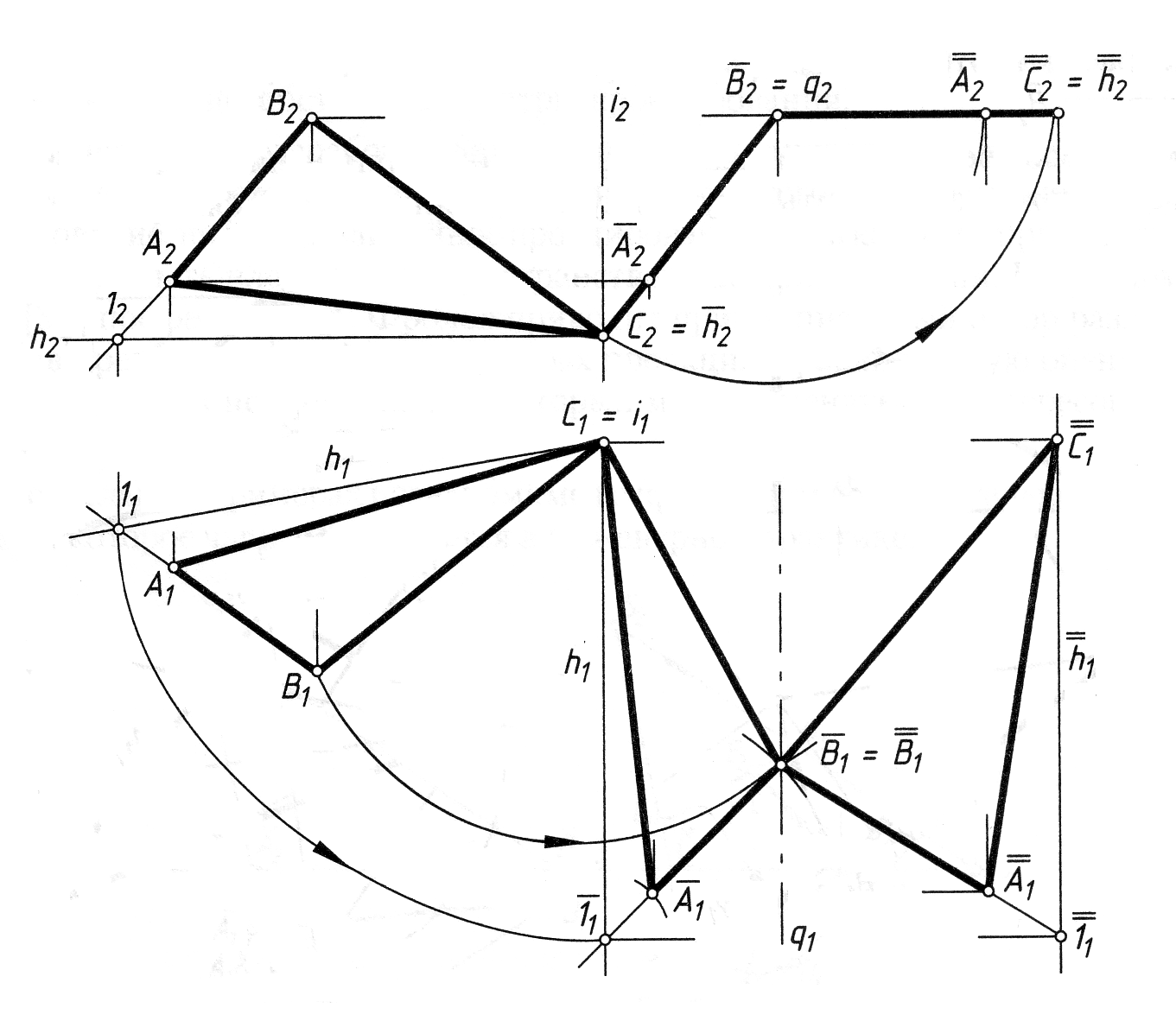
Рис. 4.13

Перетворення виконуємо послідовним подвійним обертанням. Спочатку перетворюємо площину загального положення в проеціюючу площину. Для цього в площині АВС проводимо одну із ліній рівня – h або f і обертаємо її до положення, коли вона стане перпендикулярною площині проекцій. При цьому лінія рівня спроеціюється в точку, а площина – в лінію.

Потім площину обертаємо навколо іншої проеціюючої прямої до положення, коли площина стане паралельною площині проекцій. На цю площину вона спроеціюється в натуральну величину.