Запитання і завдання для самоперевірки

1. Яке взаємне положення можуть займати пряма і площина? дві площини?

2. Яка умова паралельності прямої і площини? двох площин?

3. Як взаємно розташовані однойменні сліди двох паралельних між собою площин?

4. Чи є ознакою взаємного перетину двох площин перетин хоча б одної пари їх однойменних слідів?

5. Як визначити взаємне положення прямої і площини?

6. Як будується точка перетину прямої лінії з площиною, перпендикулярною до одної чи до двох площин проекцій?

7. Показати приклади і алгоритм визначення точки перетину прямої з площиною загального положення і проеціювальною площиною.

8. Як будується лінія перетину двох площин, з яких хоча б одна перпендикулярна до П₁ або П₂?

9. В чому полягає загальний метод побудови лінії перетину двох площин?

10. Як розміщуються проекції перпендикуляра до площини?

11. Як провести перпендикуляр з точки на пряму загального положення?

12. Як побудувати взаємно перпендикулярні площини?

13. Як визначити кут нахилу площини до площини проекцій?

Лекція № 4. Способи перетворення проекцій

План: Перетворення комплексного креслення. Суть перетворення комплексного креслення. Спосіб заміни площин проекцій. Спосіб обертання навколо вертикальних осей та прямих рівня. Плоско-паралельне переміщення.

Виклад основного матеріалу: У кресленні доводиться визначати справжні розміри фігури (наприклад, фігури перерізу тіла площиною) або її окремих елементів (наприклад, визначення справжніх величин ребер піраміди для побудови розгортки її поверхні). Фігура, розміщена паралельно будь-якій площині проекцій, проеціюється на неї в справжню величину. Перетворення проекцій дає змогу перевести задану фігуру із загального в окреме положення щодо площини проекцій.

Це досягається способом заміни площин проекцій, способом обертання або плоско-паралельним переміщенням.

Спосіб заміни площин проекцій

Cпосіб заміни площин проекцій полягає у введенні додаткових площин проекцій (П₄, П₅,…) таким чином, щоб плоский геометричний образ не змінюючи розташування в просторі, опинився в якомусь особливому положенні (зокрема, в положенні рівня чи проеціюючому) в новій системі площин проекцій. Тобто положення точок, ліній, плоских фігур у просторі залишається незмінним, а задана система площин проекцій доповнюється іншими, які утворюють з базовими площинами або між собою систему взаємно перпендикулярних площин.

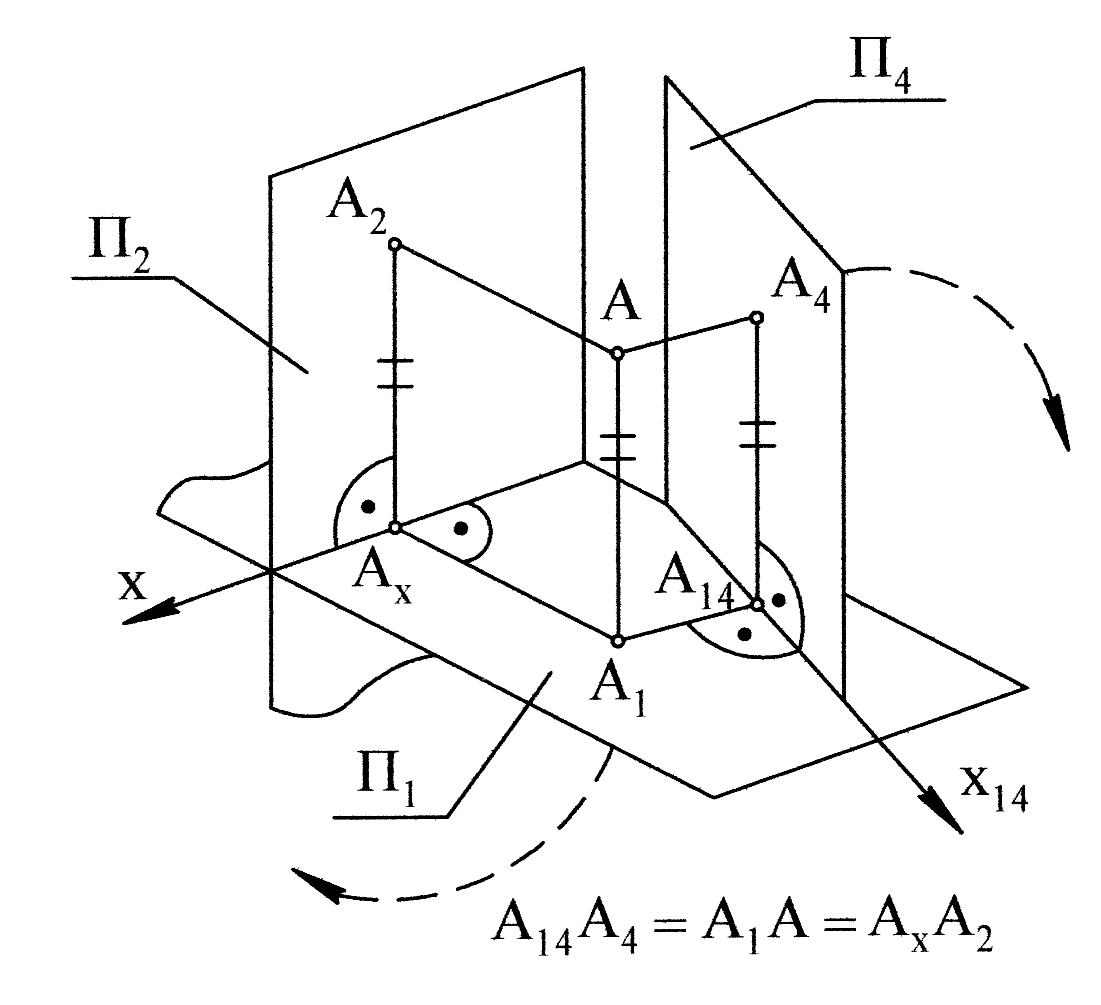
Рис. 4.1

На рис. 4.1 наведено просторову схему отримання комплексного креслення точки А в системі площин П₁П₄. Нова площина П₄ bП₁. Під час проеціювання точки А на П₄ отримаємо нову проекцію А₄, фігура АА₁А₁₄А₄ – прямокутник, площина якого перпендикулярна новій вісі. Обертанням навколо осі Х₁₄ сумістимо площину П₄ із П₁. Обертанням навколо осі Х сумістимо площину П₁ (і П₄) з площиною П₂. Від комплексного креслення точки А в системі (П₁П₂) перейшли до комплексного креслення точки А в системі (П₁П₄), замінили площину П₂ на площину П₄, замінили А₂ на А₄ (рис. 4.2). Відкладений відрізок А₄А₁₄ дорівнює відстані заміненої проекції від попередньої осі ОХ (координата Z). У разі заміни фронтальної площини проекцій П₂ на нову площину П₄ горизонтальна проекція точки А₁ не змінюється.

Рис. 4.2 Рис. 4.3

У ряді випадків потрібно проводити заміну двох площин проекцій. Таку заміну показано на рис. 4.3. Спочатку відбувається перехід від комплексного креслення в системі (П₁П₂) до комплексного креслення в системі (П₂П₄), а потім ще один перехід до комплексного креслення в системі (П₄П₅).

У разі заміни горизонтальної площини проекцій П₁ на нову площину П₄ фронтальна проекція точки А₂ не змінюється (рис. 4.3).

Для побудови нової горизонтальної проекції А₄, треба з А₂ опустити перпендикуляр на нову вісь Х₂₄ і відкласти на ньому відрізок А₂₂А₄, що дорівнює координаті Y.

Під час заміни однієї з площин проекцій необхідно керуватись такими правилами:

1)  Залежно від умови задачі вибираємо нову площину проекцій. Лінія перетину нової площини з незмінною площиною проекцій є новою віссю проекцій.

2) Через незмінну проекцію точки проводимо нову лінію зв’язку перпендикулярну до нової осі проекцій.

3) На новій лінії зв’язку від нової осі проекцій відкладаємо координату проекції, яка замінюється (відстань від точки до незмінної площини проекцій). На рис. 4.4 наведено приклад послідовності заміни площин проекцій.

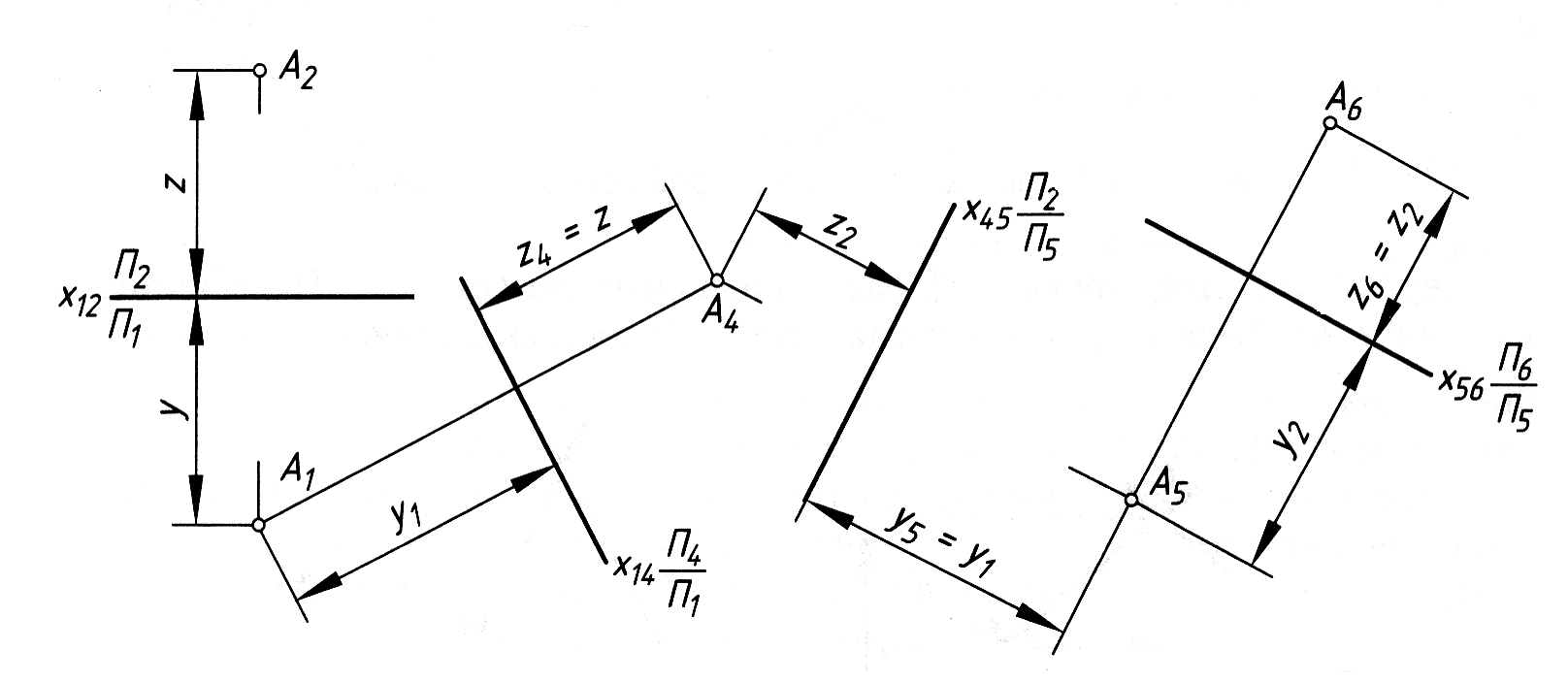
Рис. 4.4

Розглянемо розв’язок задач нарисної геометрії (метричних та позиційних) із застосуванням даного методу.

Задача 1. Знайдіть натуральну величину відрізка прямої АВ та кут нахилу до площини проекцій П₁.

Відрізок прямої АВ загального положення. Довжини відрізків А₁В₁ і А₂В₂ менші довжини відрізка АВ. Для того щоб визначити його довжину, необхідно провести додаткове проеціювання на допоміжну площину, якій він буде паралельний.

Для цього введемо нову площину проекцій П₄ паралельно відрізку АВ і перпендикулярно П₁. При цьому нова вісь Х₁₄ буде паралельна А₁В₁ (рис. 4.5). Кут нахилу відрізка АВ до площини проекцій П₄ рівний нулю, і АВ на П₄ проеціюється в натуральну величину, тобто А₄В₄=АВ. Вимірявши відрізок А₄В₄, отримаємо довжину відрізка АВ. На площині П₄ отримаємо кут нахилу α до площини проекцій П₁.

Рис. 4.5

Задача 2. Перетворити пряму загального положення в проеціюючу пряму.

Нехай h (h₁,h₂) – горизонталь (рис. 4.6). Уведемо нову площину проекцій П₄ перпендикулярно h. Горизонталь паралельна П₁, тоді П₄ буде перпендикулярно П₁. На площину П₄ горизонталь буде проеціюватися у точку.

Рис. 4.6

Використовуючи розв’язок попередньої задачі, можна провести проеціювання прямої загального положення m в точку (рис. 4.7)

Рис. 4.7

Введемо нову площину проекцій П₄ паралельно m і перпендикулярно до П₁. За новими проекціями двох точок 1 і 2 прямої m знайдемо m₄. У новій системі площин (П₁П₄) пряма m є лінією рівня, вона паралельна П₄. Тепер, використовуючи розв’язок попередньої задачі (рис. 4.6), проеціюємо пряму m у точку. Для цього вводимо нову площину проекцій П₅ перпендикулярно прямій m і перпендикулярно П₄. Пряма m на П₅ буде проеціюватися у точку.

Задача 3. Визначити натуральну величину АВС. АВС – площина загального положення (рис. 4.8).

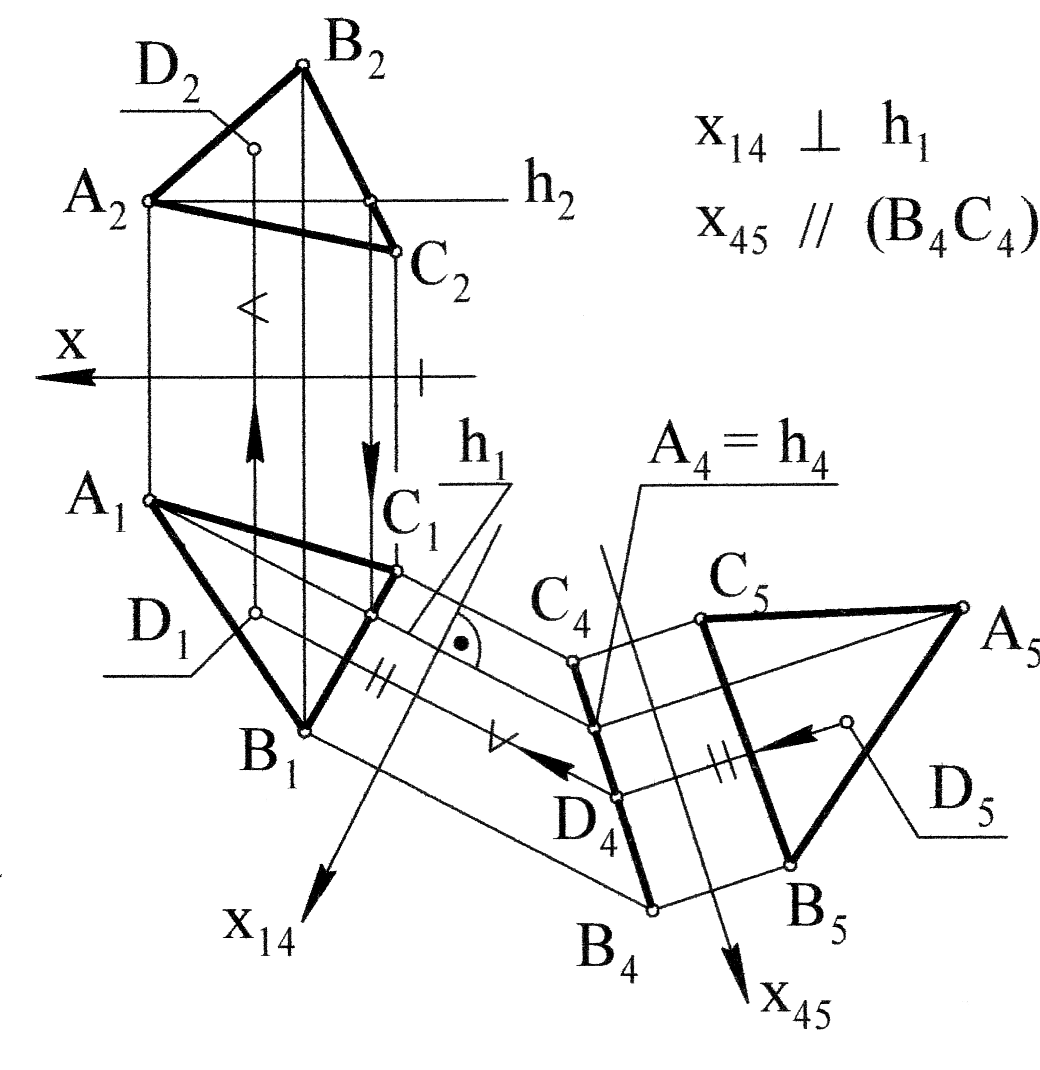
Рис. 4.8

Під час розв’язування цієї задачі необхідно виконати подвійне перетворення (подвійну заміну площин проекцій): спочатку перетворити площину загального положення в проеціюючу площину, а потім проеціюючу площину в площину рівня.

1) Проводимо лінії рівня площини – h і f.

2) Вибираємо П₄  h; ₄  ₁, ₄  ₁ = X₁₄; X₁₄  h₁.

В системі (П₁П₄) горизонталь стане проеціюючою прямою, а площина АВС – проеціюючою площиною.

3) П₅||АВС; П₅  П₄, П₅  П₄ = Х₄₅; Х₄₅ || А₄В₄С₄; А₅В₅С₅ – натуральна величина АВС.

На рис. 4.8 за проекцією точки D₅ (одна точка натуральної величини фігури) знайдені решта проекцій. Проекція D₄ належить прямій, в яку проеціюється площина АВС. Послідовність побудов вказано стрілками.