Запитання і завдання для самоперевірки

1. Які є способи задання і зображення площини на епюрі?

2. Що таке сліди площини на площині проекцій?

3. Які площини називаються площинами рівня та які їх властивості?

4. Які площини називаються проеціювальними та які їх властивості?

5. Які лінії називаються головними лінями площини?

6. Як розташовуються на епюрі проекції горизонталі, фронталі?

7. Які лінії називаються лініями найбільшого нахилу?

6. Сформулюйте умови належності прямої площині.

Лекція №3 (частина 2). Зображення площин. Взаємне положення формоутворюючих елементів простору

Перетин прямої з площиною. Перетин двох площин. Паралельність прямої та площини. Паралельність двох площин

Загальним випадком взаємного положення прямої і площини є їх перетин. Якщо точка перетину знаходиться у нескінченності, то пряма і площина паралельні між собою.

В залежності від взаємного положення прямої і площини, площин відносно площин проекцій і відносно одна одної можливі наступні випадки:

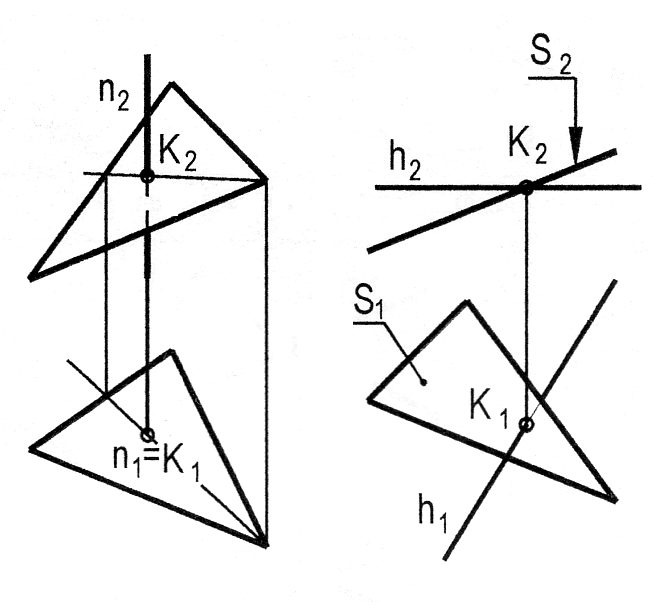
Випадок 1. Перетин прямої  загального положення з проеціюючою площиною   ₂ (рис. 3.13).

   = К(К₁; К₂). Проекція точки перетину прямої  з площиною  на П₂ – К₂ визначається відразу: ₂  ₂ = К₂. За допомогою лінії зв’язку визначаємо горизонтальну проекцію точки К – К₁, виходячи з умови належності точки К прямій . Видимість на П₁ визначаємо за допомогою точок 1 і 2, конкуруючих відносно площини проекцій П₁.

   = К(К₁; К₂). Проекція точки перетину прямої  з площиною  на П₂ – К₂ визначається відразу: ₂  ₂ = К₂. За допомогою лінії зв’язку визначаємо горизонтальну проекцію точки К – К₁, виходячи з умови належності точки К прямій . Видимість на П₁ визначаємо за допомогою точок 1 і 2, конкуруючих відносно площини проекцій П₁.

Рис. 3.13

Випадок 2. Перетин проеціюючої прямої ₁ з площиною (a  b) загального положення (рис. 3.14).

   = K. ₁  K₁; K  , K  ; K  12; 12  . Видимість на П₂ визначаємо за допомогою конкуруючих точок 3 і 4.

Рис. 3.14

Паралельність прямої і площини

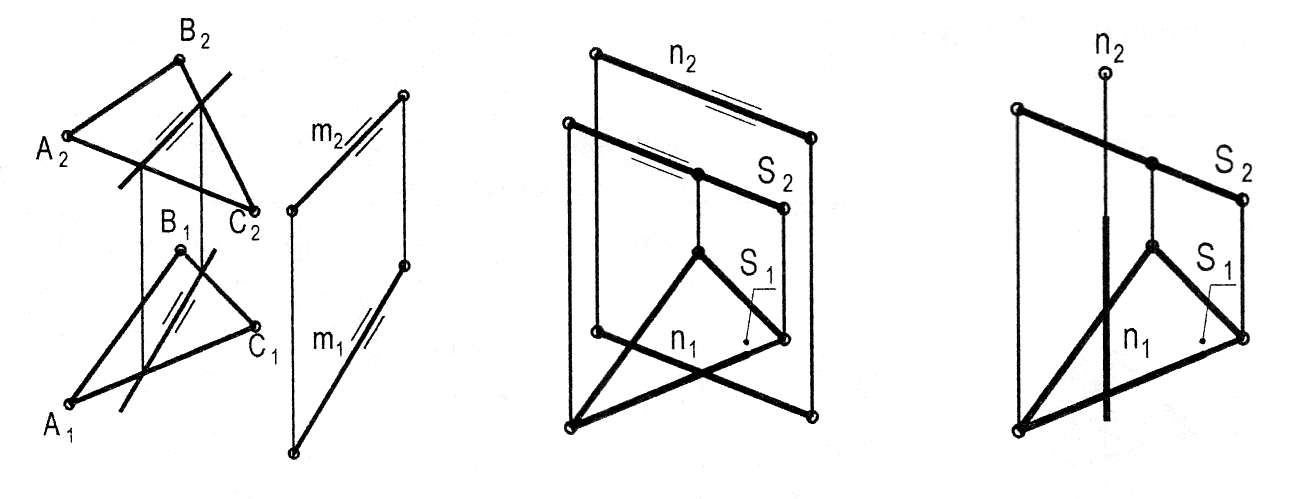
Пряма паралельна площині, якщо вона паралельна якій-небудь прямій, розміщеній на цій площині. Приклади паралельності прямої та площини наведено у таблиці 3.2.

Таблиця 3.2

Паралельність прямої та площини

Пряма та площина займають загальне положення	Площина займає часткове положення	Пряма та площина займають часткове положення

Якщо через точку в просторі треба провести пряму, паралельну площині, то спочатку в цій площині проводимо яку-небудь пряму, а потім через задану точку проводимо другу пряму, паралельну першій.

Приклад 1. Через точку М простору провести пряму , паралельну заданій площині (АВС) (рис. 3.15).   M;  || : проводимо довільну пряму 12, яка належить площині ; проводимо пряму  || 12  ₁ || 1₁2₁; ₂ || 1₂2₂.

Рис. 3.15

Приклад 2. Задана площина (h⁰  f⁰) і точка М. Через точку М провести пряму , паралельну заданій площині  і площині проекцій П₁ (рис. 3.16).

Ч ерез М₁ проводимо ₁ || h₁⁰; через М₂ – ₂ || h₂⁰   || h.

Рис. 3.16

Перетин двох площин, перпендикулярних до однієї з площин проекцій

Д ві площини, перпендикулярні до якої-небудь площини проекцій, перерізаються по прямій, яка перпендикулярна до тієї самої площини проекцій (рис.3.17).

Рис. 3.17 Рис. 3.18

  П₂,  П₂,    = і, і  П₂, і₂ – точка, і₁ –  Х₁₂.

Перетин двох площин, перпендикулярних до різних площин проекцій

Дві площини, які перпендикулярні до різних площин проекцій, перерізаються по прямій, проекції якої збігаються зі слідами-проекціями площин (рис. 3.18).

(  АВС )  П₁ , (DEF)  П₂ .

   = n; n₁  ₁; n₂  ₂.

Перетин площини  проеціюючого положення з площиною 

загального положення (рис. 3.19)

  П₂, (DEF); (АВС).    = n. n  ; n  ; n₂  ₂; пряму n фіксуємо двома точками – 1 і 2, які є спільними для обох площин, що перетинаються. Видимість площин  і  визначаємо на П₁ за допомогою конкуруючих точок 3 і 4.

Р ис. 3.19

Перетин прямої  загального положення з площиною  загального положення (рис. 3.20 і 3.21)

На рис. 3.20 зображені площина  і пряма , що перетинається з цією площиною. Проведемо через пряму  площину . Якщо знайти пряму MN перетину площин  і , то точка перетину прямих  та MN буде точкою, в якій пряма  перетинається з площиною . Цю точку (К) часто називають точкою зустрічі прямої з площиною.

Таким чином, побудова точки зустрічі прямої загального положення з площиною загального положення складається з трьох операцій:

1 ) Проведення через задану пряму  допоміжної площини- посередника . Як допоміжні, звичайно, використовують проецію-ючі площини внаслідок простоти, з якою здійснюється проведення цих площин через прямі лінії на комплексному кресленні – завдяки збиральній властивості одного зі слідів-проекцій таких площин.

Рис. 3.19

2) Знаходження лінії MN перетину заданої площини  з допоміжною площиною посередником .

3 ) Визначення точки К перетину заданої прямої  зі знайденою лінією перетину двох площин. Точка К є шуканою точкою перетину прямої  з площиною .

Рис. 3.20

На комплексному кресленні (рис. 3.20) задачу розв'язуємо в такому порядку:

1)   ;   ₂;

2)    = MN; M  AC; N  BC;

3) MN   = К; M₂N₂  ₂; M₁N₁ ₁ = K₁; K₂  ₂.

4) Видимість прямої  по відношенню до площини  на П₁ і П₂ визначаємо за допомогою конкуруючих точок 1 i M; 2 і 3.

У таблиці 3.3 наведено приклади перетину прямої з площиною.

Таблиця 3.3

Перетин прямої з площиною

Пряма і площина займають загальне положення	Один елемент займає часткове положення	Пряма і площина займають часткове положення
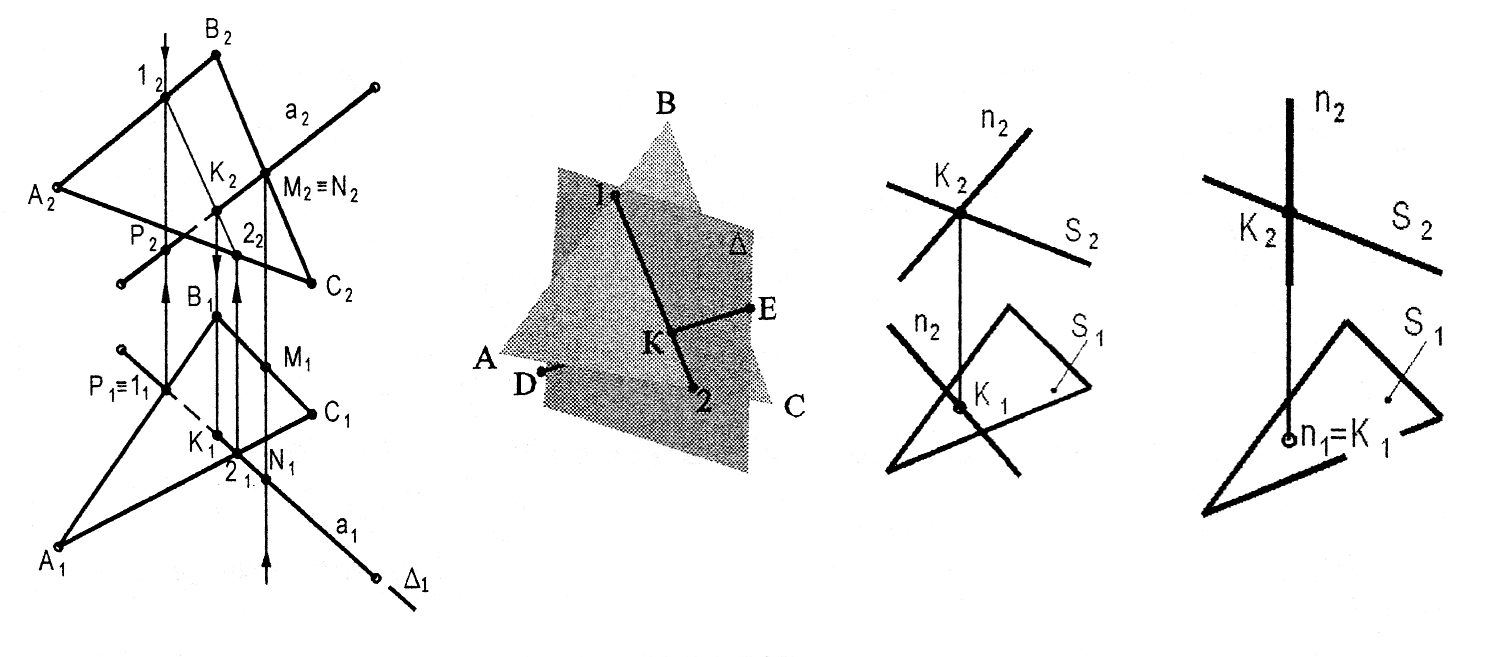
Алгоритм рішення: 1) а  ;   1; 2)    (АВС) = 1-2; 1  AВ; 2  АC; 3) 1-2  а = К; 1122  а1; 1222  а2 = K2; K2  а2; 4) Визначаємо видимість прямої та площини.