5.3 Диференціальна функція розподілу випадкової величини

Розглянемо неперервну випадкову величину Х з функцією розподілу F(x). Обчислимо ймовірність влучення цієї випадкової величини на ділянку від до

.

Розглянемо відношення цієї ймовірності до довжини ділянки, тобто середню ймовірність, що приходиться на одиницю довжини цієї ділянки, і будемо наближувати до нуля, тобто перейдемо до границі при Отримаємо похідну від функції розподілу

Позначимо f( ) = Функція f( ) показує, як щільно розподіляються значення випадкової величини в інтервалі від до . Звідки і її назва – щільність розподілу випадкової величини. Інша назва – диференціальна функція розподілу.

Ця функція існує тільки для неперервної випадкової величини.

Із наведених формул виходить, що ймовірність влучення значення випадкової величини на проміжок дорівнює

Величину називають елементом ймовірності. Геометрично це є площа елементарного прямокутника з висотою, що дорівнює і основою .

f(x)

f(x)dx

0 x

X₁ x x+dx x₂

Ймовірність влучення випадкової величини в довільний інтервал від дорівнює сумі елементів ймовірності на цій ділянці, тобто інтегралу

.

Геометрично ймовірність влучення величини на ділянку ( ) дорівнює площі криволінійної трапеції, обмеженою кривою і прямими .

Таким чином, неперервну випадкову величину одночасно характеризують дві взаємозалежні функції – диференціальна (щільність розподілу) та інтегральна. Знаючи хоча б одну з них, ми можемо відповісти на найбільш важливе практичне питання: з якою ймовірністю досліджувана випадкова величина набуває значення з того чи іншого інтервалу. Ця ймовірність дорівнює

Ця формула лежить в основі розв‘язання більшості ймовірно – статистичних задач.

Властивості диференціальної функції:

1. Геометрично це означає, що крива розподілу завжди лежить не нижче осі абсцис.

2. Дійсно, цей інтеграл є ймовірністю того, що випадкова величина Х набирає значень з інтервалу ( ) . Така подія достовірна. Ймовірність її дорівнює одиниці. Геометрично це означає, що вся площа під кривою розподілу дорівнює одиниці.

Визначимо щільність розподілу для випадкової величини, заданої в попередньому прикладі інтегральною функцією

F (x) =

Диференцюючи F (x) одержимо:

(x) =

f(x)

0,5

0,25

-2 0 2 4 x

На всякому інтервалі зміни випадкової величини Х щільність розподілу постійна. Такий вид розподілу називається законом рівномірної щільності.

Покажемо тепер. Як може бути отримана щільність розподілу випадкової величини практичним шляхом.

§6.Побудова статистичного розподілу кількісної оцінки (елементи математичної статистики)

6.1. Сутність вибіркового методу.

Побудова варіаційних рядів.

Побудова гістограм.

Згадаємо деякі фізико - механічні властивості гірського масиву. Внаслідок неоднорідності породного масиву більшість з кількісних ознак, що йому належать,є випадковими величинами. Наприклад,у результаті випробування зразків гірської породи на стиск ми одержуємо для кожного зразка різні значення міцності, що обумовлено випадковими причинами. Тобто,міцність породи на стиск - випадкова величина, що може приймати значення з дуже широкого інтервалу. І виникає питання, які значення досліджуваної ознаки найбільш ймовірні, як оцінити наявний розкид цих значень, як він уплине на остаточні результати і таке інше. Для відповіді на ці питання треба підібрати для отриманих даних теоретичний закон розподілу у вигляді інтегральної чи диференціальної функцій розподілу. Першим кроком на шляху підбору теоретичного розподілу є статистична обробка даних,тобто їх статистичний аналіз.

З обстежуваної генеральної сукупності однорідних об’єктів,кількість яких N, роблять випадкову вибірку чисельністю в n одиниць. Нехай досліджується міцність деякої гірської породи на одноосьовий стиск. Ця характеристика встановлюється шляхом випробування в лабораторних умовах зразків породи об’ємом V, виготовлених із проби, що у свою чергу відібрана в досліджуваному масиві гірської породи. Таким чином, застосовується вибірковий метод: з генеральної чисельності зразків (V - увесь обсяг досліджуваного масиву гірської породи) відбирається тільки n зразків. Величина n називається обсягом вибірки.

Для того щоб за даними вибірки можна було достатньо впевнено судити т про цікавлячи нас ознаки генеральної сукупності, необхідно, щоб об’єкти вибірки правильно її представляли: вибірка повинна бути показною (репрезентативною). Вибірка буде показною,якщо всі об’єкти генеральної сукупності мають рівні шанси потрапити у вибірку.

Нехай у результаті вимірювань отримано значення (варіанти) кількісної ознаки Х: . Якщо ці значення записано у у відповідній відомості або в журналі в тій послідовності, у якій вони спостерігалися в дійсності, вони називаються незгрупованими даними.

Якщо таких даних багато, то ми не в змозі охопити зміст явища. Для виявлення характерних рис досліджуваної ознаки корисно згрупувати дані. Нехай у результаті дослідів кількісної ознаки Х значення з’явилося раз, - разів, ….. - з’явилося раз.Числа (і=1,….r), що показують, скільки разів спостерігається кожне із значень ознаки, називаються частотами.

Зрозуміло,що сума частот повинна дорівнювати обсягу вибірки

Величини називають відносними частотами

__

Якщо розташувати варіанти у порядку. що зростає чи спадає, і вказати для кожної варіанти її частоту, одержимо розподіл ознаки у вигляді упорядкованого віріаційного ряду.

X			…………………..
M			…………………….
W			…………………….

Як бачимо варіаційний ряд аналогічний ряду розподілу дискретної випадкової величини, що ми розглядали раніше (у прикладі з вимикачами напруги).

У наступній таблиці наведені результати визначення межі міцності зразків алевроліту на одноосьовий стиск у вигляді незгрупованих даних.

№ зразка	Міцність зразка на стиск, _ _	№ зразка	Міцність зразка на стиск, _
1 2 3 4 5 6 7 8 9 10	183 170 176 178 176 180 176 185 184 174	31 32 33 34 35 36 37 38 39 40	172 176 167 166 180 183 176 182 178 172
11 12 13 14 15 16 17 18 19 20	168 174 189 172 175 167 179 176 169 178	41 42 43 44 45 46 47 48 49 50	185 183 175 174 180 165 169 171 178 169
21 22 23 24 25 26 27 28 29 30	169 171 170 177 176 179 174 176 188 178	51 52 53 54 55 56	170 179 171 178 173 177

Але якщо для цих даних побудувати варіаційний ряд він вийде дуже громіздким. Тому не будемо його робити, а побудуємо так званий інтервальний ряд. Цей ряд використовують, коли випадкова величина є неперервною або число різних варіант дискретної величини Х велике.

Для побудови інтервального ряду треба:

1)серед незгрупованих даних вибирають найбільше і найменше .

=189 .

2)відрізок( , .)поділяють на інтервали (розряди ) довжиною L

Де k - кількість інтервалів. Це число можна вибрати довільно,а можна скористатись формулою

Візьмемо число розрядів к = 6.

При цьому довжина розряду

За початок першого розряду візьмемо . Складаємо інтервальний ряд, помічаючи кожний результат крапкою. Варіанти, які приходять на мету розрядів, будемо відносити до наступного розряду. До того будемо рахувати частоти і відносні частоти.

	165-169	169-173	173-177	177-181	181-185	185-189
Підрахунок частот	.....	.............	...............	..............	…..	….
Частоти ,mі	5	13	15	14	5	4
	0.089	0ю232	0.268	0.250	0.082	0.072
	0.022	0.058	0.066	0.062	0.022	0.018

Наочним графічним зображенням інтегрального ряду є гістограма частот. На осі абсцис відкладаються відрізки, які дорівнюють довжинам інтегралів. На кожному з відрізків як на основі будуть прямокутник висота якого складає:

Тоді площа кожного прямокутника дорівнює відносній частоті ,а площа всієї гістограми дорівнює одиниці.

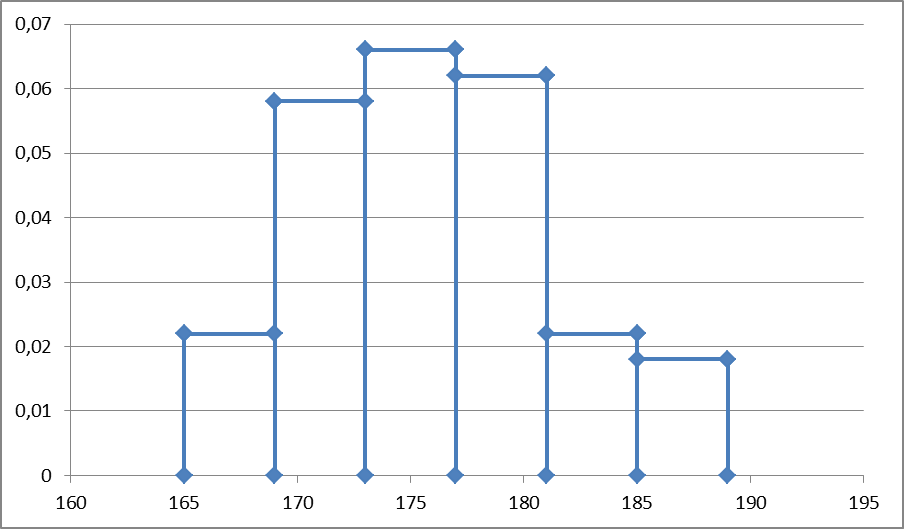
На рисунку побудована гістограма відносних частот для величини Х - міцності на стиск алевроліту. Очевидно,що при збільшенні числа дослідів можна вибирати усе більш дрібні інтервали. При цьому гістограма буде усе більше наближатися до деякої кривої,що обмежує область, площа якої дорівнює одиниці. Ця крива має назву полігон. Неважко переконатися, що ця крива являє собою графік щільності розподілу досліджуваної кількісної ознаки Х, тобто графік функції f(х).

Подальший аналіз складається в підборі аналітичного виразу для функції f (х). При цьому дослідник аналізує вигляд гістограми, що у першому наближенні вказує на вигляд графіка f (х). І на цьому етапі головну роль відіграють так звані числові характеристики випадкової величини.