§ 5. Випадкові величини.

5.1. Дискретні та неперервні випадкові величини.

Випадкову величину задають областю можливих значень та ймовірністю появи їх. Випадкові величини позначаємо буквами X ,Y, Z, а їхні можливі значення - x, y, z .

Випадковою називається величина, значення якої наперед невідомі і які можуть бути визначені лише внаслідок досліду. Випадкові величини поділяються дискретні та неперервні.

Дискретною випадковою величиною називається величина, можливі значення якої можуть бути пронумеровані в якомусь порядку і записані у вигляді послідовності. Тобто ,усі значення випадкові величини можна перелічити.

Приклад - кількість відбійних молотків, що виходять з ладу протягом зміни .

Якщо випадкова величина в ході досліду приймає будь-яке значення з деякого інтервалу ,вона називається неперервною.

Приклад - тиск рідини ,яка тече в трубі, похибки вимірювань.

Розглянемо дискретну випадкову величину Х з її можливими значеннями Кожного з них величина Х набуває з деякою ймовірністю ,а саме: значення - з ймовірністю ; значення - з ймовірністю ; значення - з ймовірністю .

Події несумісні і утворюють повну групу. Отже, сума ймовірностей цих подій дорівнює одиниці:

.

Ця сумарна ймовірність певним чином розподілена між окремими значеннями випадкової величини Х.

Визначення. Усяка відповідність між значеннями випадкової величини й ймовірностями, з якими ці значення з’являються, називається законом розподілу.

Найпростішою формулою завдання закону є таблиця,яка містить значення випадкової величини і відповідні їм ймовірності. Така таблиця називається рядом розподілу

Х			……………………
Р			……………………

Приклад . На шахті протягом 100 змін фіксувалася кількість вимикачів_напруги, що виходять з ладу з різних причин. Результати спостережень наведено в таблиці,що являє собою ряд розподілу для випадкової величини Х- вимикачів напруги, що вийшли з ладу протягом робочого часу.

Таблиця.

Кількість що вийшли з ладу протягом робочого часу	Кількість спостережень m	Відносні частоти w
0 1 2 3 4	16 56 24 3 1	0.16 0.56 0.24 0.03 0.01

Щоб додати ряду розподілу наочність будують так звану полігональну криву: по осі абсцис відкладають значення випадкової величини,по осі ординат- ймовірність цих значень(у нас відносні частоти.

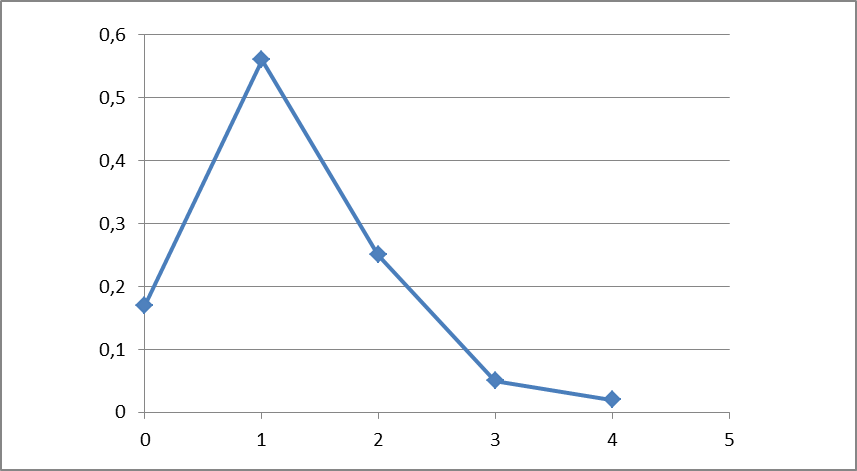
Із наведеного приклада видно, що в умовах даної шахти найбільш ймовірним є вихід з ладу одного вимикача протягом робочого часу.

5.2.Інтегральна функція розподілу.

Ряд розподілу вичерпно характеризує дискретну випадкову величину. Але для неперервної випадкової величини побудувати такий графік ми не можемо ,оскільки ми не можемо перелічити всі її можливі значення. Для неперервної випадкової величини має сенс говорити тільки про ймовірність того, що вона приймає значення з деякого, нехай навіть дуже малого інтервалу.

Тому для кількісної характеристики розподілу неперервної величини розглядають не ймовірність події Х = х, а ймовірність події Х < х. Зрозуміло, що ймовірність цієї події залежить від значення х, тобто є функцією х. Ця функція називається функцією розподілу випадкової величини і позначається F(x)

F(x)=P (X <x).

Функція розподілу є універсальною формою закону розподілу і придатна для опису і неперервних і дискретних величин.

Властивості функції розподілу:

1.Всі значення інтегральної функції належать відрізку [0;1] (як ймовірності)

0 ≤ F(x) ≤ 1

2.F( x ) - неспадна функція свого аргументу, тобто,

якщо

Із цієї властивості випливає наслідок:

Ймовірність того, що випадкова величина отримає значення, що належить до інтервалу ( ),дорівює приросту функції на цьому інтервалі:

3.Якщо можливі значення випадкової величини належать інтервалу (а; в),то:

а) F(x)=0 при х ≤ а ( ймовірність події х=а, дорівнює нулю, оскільки ця подія неможлива);

б) F(x)=1 при x ≥ в (ймовірність події "Х> в", а отже , і значення функції в точці х=в, дорівнює одиниці,оскільки ця подія - достовірна).

Для дискретної випадкової величини графік інтегральної функції має східчастий вигляд. Побудуємо інтегральну функцію F(x) для задачі про вимикачі напруги.

Х	0	1	2	3	4
Р	0.16	0.56	0.24	0.03	0.01

X ≤ 0 F (x) = 0

0 < x ≤ 1 F (x) = P (x < 1) = 0.16

1 < x ≤ 2 F (x) = P (x < 2) = 0.16 + 0.56 = 0.72

2 < x ≤ 3 F (x) = P (x < 3) = 0.16 + 0.56 + 0.24 = 0.96

3 < x ≤ 4 F (x) = P (x < 4) = 0.16 + 0.56 +0.24 + 0.33 = 0.99

X > 4 F (x) = 1

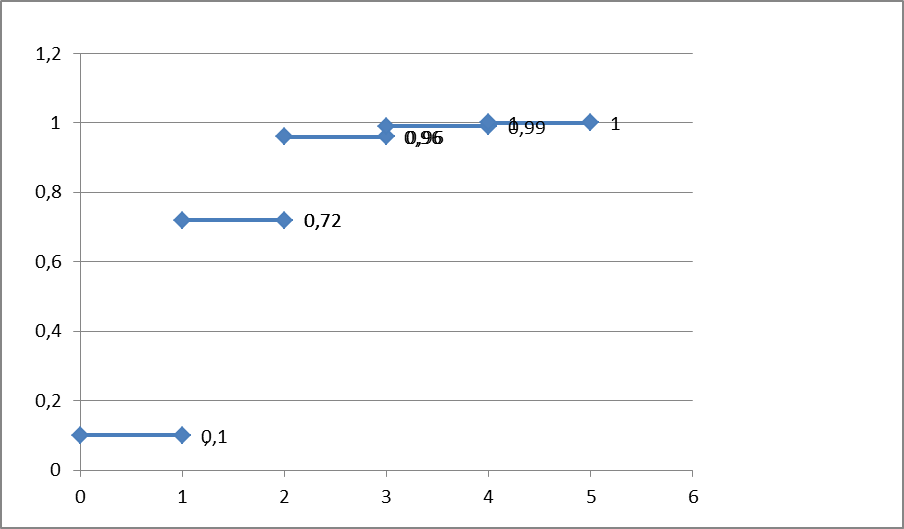
Коли змінна X проходить через дискретні значення 0; 1; 2; 3; 4, інтегральна функція змінюється стрибко подібно, причому величини стрибків дорівнюють ймовірностям цих значень ( відповідно 0,16; 0,56; 0,24; 0,03; 0,01 ). Сума всіх стрибків функції F (x) дорівнює одиниці.

Зі збільшенням можливих значень X кількість стрибків збільшується, а самі стрибки зменшуються. Східчаста лінія при цьому наближується до плавної кривої. Для неперервної випадкової величини графік інтегральної функції – неперервна лінія.

Приклад. Випадкова величина X задана функцією розподілу

F (x) =

Знайти ймовірність того, що в результаті іспитів випадкова величина прийме значення

а) з інтервалу ( 2,5; 3,0 );

б) не менше 3.

Графік інтегральної функції має вигляд

P(x)

1

0,5

-2 0 2 4 6 x

а)

б) Події X - протилежні.

. Тоді